牛顿法、指数分布

http://blog.csdn.net/v1_vivian/article/details/52038037

《Andrew Ng 机器学习笔记》这一系列文章文章是我再观看Andrew Ng的Stanford公开课之后自己整理的一些笔记，除了整理出课件中的主要知识点，另外还有一些自己对课件内容的理解。同时也参考了很多优秀博文，希望大家共同讨论，共同进步。

网易公开课地址：http://open.163.com/special/opencourse/machinelearning.html

本篇博文涉及课程四：牛顿方法

主要内容有：

（1）牛顿法（Newton's Method）

（2）指数分布族

（3）广义线性模型（GLMS）  （下篇博文具体分析）

（4）多项式分布                      （下篇博文具体分析）

牛顿法

牛顿方法也是对解空间进行搜索。

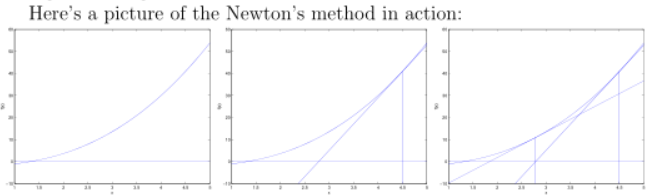
基本思想： 对于函数f(x)，如果我们要找到使得函数值为0的x值时，做法如下：

1、随机选一个点（θ0），然后求出该点的切线，即导数。

2、延长它使之与x轴相交，以相交时的x的值（θ1）。

3、重复1、2直到f(x)==0

我们可以得知：其中θ的更新规则为：

对于机器学习问题，我们优化的目标函数为极大似然估计函数，当极大似然估计函数取得最大时，其导数为0。

所以，我们可以使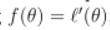得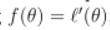，由此可得：

上面是当参数θ为实数时的情况，当参数为向量时，更新规则为：（其中，H是一个n*n的矩阵，n为参数向量的长度，即特征数，H是函数的二阶导数矩阵，被称为Hessian矩阵，此时，用一个表示一阶导数的向量乘上一个表示二阶导数的矩阵的逆，来表达上式中的一阶导数除以二阶导数）

                                                                                                               

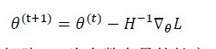
H矩阵中元素Hij计算公式如下：

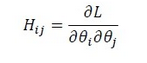
牛顿方法的优点：

牛顿方法与梯度下降方法功能一样，都是在寻到解空间，但相比较而言，牛顿方法的优点是收敛速度快，通常只要经过十几次迭代就可以达到收敛。牛顿方法也被称为二次收敛，因为当迭代到距离收敛值比较近的时候，每次迭代都能使误差变为原来的平方。

牛顿方法的缺点：

牛顿方法的缺点是当参数向量较大时，每次迭代都需要计算一次Hessian矩阵的逆，比较耗时。

指数分布族

指数分布族是指可以表示为指数形式的概率分布。指数分布族的形式如下:（其中，η称为分布的自然参数（nature parameter）；T(y)是充分统计量（sufficient statistic），通常T(y)=y。当参数a、b、T都固定时，就定义了一个以η为参数的函数族）：

以将高斯分布和伯努利分布为例，我们将它们表示称为指数分布族的形式。

1.将伯努利分布写成指数分布族的形式

伯努利分布是对0,1问题进行建模的分布，它可以用如下形式表示：

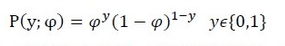
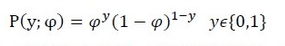
将其转换形式：

此时，我们就将伯努利分布表示成了指数分布族的形式；其中：

我们可以看到，φ的形式与logistic函数一致，这也正是因为logistic模型对问题的概率估计是伯努利分布的缘故。

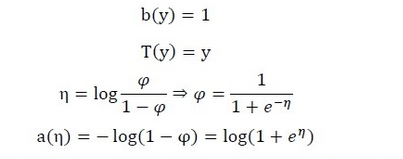
2.将高斯分布写成指数分布族的形式

由高斯分布可以推导出线性模型，由线性模型的假设函数可知，高斯分布的方差 σ² 与假设函数无关，所以简便起见，我们可以将σ²的值设为1，推导过程如下：

此时，我们就将高斯分布表示成了指数分布族的形式；其中：

                                

实际上，大多数概率分布都可以表示成指数分布族的形式。比如：

（1）伯努利分布：对0、1问题进行建模；

（2）多项式分布：多有K个离散结果的事件的建模；

（3）泊松分布：对计数过程进行建模，比如网站访问量的计数问题，放射性衰变的数目，商店 顾客数量等问题；

（4）伽马分布与指数分布：对有间隔的正数进行建模，比如公交车的到站时间问题；

（5）β分布：对小数建模；

（6）Dirichlet分布：对概率分布建模；

（7）Wishart分布：协方差矩阵的分布；

（8）高斯分布；