机器人碰撞检测几何模型设计

来源 | 混沌无形

作者 | 混沌无形

摘要：

机器人的碰撞检测等效几何模型设计的优劣对轨迹规划算法效率有着非常大的影响，本文以car-like robot为例，对比分析了5种不同等效模型构型的优缺点及适用对象，并介绍了基于IFL模型的设计及优化过程，最终通过数值遍历方法计算得到真实机器人的等效几何模型参数。

-引言-

在前面的运动规划系列文章《机器人运动规划算法研究现状简述》中概述了各种类型的规划算法，但暂时还没有拿出一种规划算法来剖析，为了后续的剖析做铺垫，本文先介绍机器人碰撞检测几何模型的选择及设计优化方法。

做轨迹规划算法和机器人碰撞检测几何模型有什么关系？为什么要做机器人碰撞检测几何模型？ 

我们在做轨迹规划算法时，是需要保证机器人沿着计算出来的轨迹运动不会和周围的障碍物发生碰撞的，该约束条件对应于图 1.1所示的避障约束，具体来说，就是机器人需要在非常短的规划周期内生成一条无碰撞的轨迹，同时在沿着规划的轨迹运动过程中要动态更新。

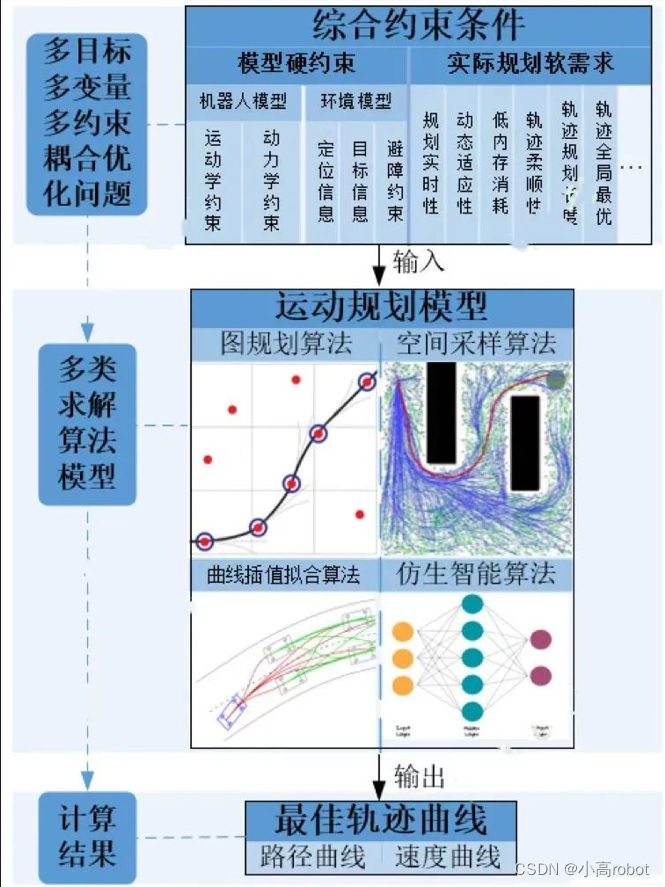
图 1.1 运动规划通用模型

那避障约束和机器人碰撞检测几何模型有什么联系吗？ 

从上面分析可知，避障约束是需要计算出此刻机器人与障碍物之间的（最短）距离的，以图 1.2为例，实际应用中，机器人的外形往往是非常复杂且不规则的，想要精确计算出机器人与周围障碍物的距离所花费的计算成本是非常大的。

图 1.2 运动规划示意图

对照图 1.3，可以细分下这个计算成本在哪儿： 

其一机器人外形复杂、环境中的障碍物外形也很复杂，想要精确描述机器人、环境及障碍物的几何外形，就需要很庞大的数学公式集合，还需要计算出机器人与障碍物的距离，这个计算量也很大，我们可以假设该计算量为NC； 

其二，一条轨迹理论上是可以离散化为无数多的路径点的，理论上应该保证机器人位于这“无数多”的路径点上都不能和障碍物有碰撞，所以要将机器人依次模拟放在这些路径点上挨个计算出与障碍物的距离，并判断该距离是否满足最小阈值条件，假如该条轨迹被离散化为MC个点，意味着一条轨迹的计算量是NC×MC； 

其三，我们在轨迹规划过程中，可能会事先生成众多的候选轨迹（如DWA算法），然后计算每一条候选轨迹的总成本，最终选择总成本最低的轨迹，而碰撞检测就是总成本之一，假设候选轨迹每次会生成QC条，这就意味机器人每做一次规划，仅碰撞检测这块的计算量就是NC×MC×QC，这是非常大的计算量！

 

 图 1.3 机器人几何模型

而机器人在运动过程中，因为自身位置及环境都在动态变化，所以碰撞检测以非常高的频率在执行，所以降低碰撞检测的计算成本是非常利于提升运动规划算法的效率的。 

从以往经验可以看出，碰撞检测往往占据了运动规划模型中比较大的计算量，所以从上面的公式可以分析出，如果我们降低了NC、MC和QC中的任意一个，都将极大降低运动规划的计算成本。 

所以本文所介绍的内容就是降低单次碰撞检测的计算量NC。 

降低NC的思路很简单：简化机器人的几何外形，当然需要尽可能保证简化后的几何模型和机器人外来的外形差异不大。 

笔者之前主要做轮式机器人相关的研究，所以本文也将以car-like robot为例来分析，同时对比不同类型的轮式移动机器人的几何模型的优劣。

-模型构型分析-

如图 2.1所示，机器人外形是立体的，复杂且不规则，若直接应用于运动规划模型，会增加不必要计算成本。由于机器人的运动规划在二维平面，因此可综合考虑机器人俯视投影的轮廓形状、安全碰撞余量等因素，优化设计简洁的机器人等效几何模型。

（a）机器人模型 

 （b）机器人样机

图 2.1 机器人物理样机“MCR”

如图 2.2 所示，机器人立体外形不规则，但俯视图（虚线框图）的外边界近似于矩形（灰色矩形）。常见的用于等效复杂的机器人外轮廓的简易几何模型共有5种，按照几何特征可大致分为三类：多边形构型（a）、圆形构型（b）及复合构型（c）。 

为评估图 2.2 中常用构型的适用性，主要评价指标为： 

贴合紧凑性：即机器人外轮廓边界与等效几何模型边界的综合贴合距离； 

贴合均匀性：即机器人外轮廓与等效模型边界的间距变化程度； 

计算复杂度：即规划模型中的机器人与障碍物之间碰撞检测及碰撞距离计算复杂程度。

（a）多边形构型

（b）圆形构型

（c）复合构型

图 2.2 机器人等效几何模型构型

蓝色虚线为等效几何模型，黑色虚线表示机器人实际俯视图，该俯视图也被称为FootPrint，是足迹的意思，表示机器人运动过程留下的足迹，本质上就是俯视图所覆盖的区域。

分析可知，由于多边形构型与机器人轮廓相似度极高，因此多边形构型贴合紧凑性好，贴合均匀性好，但碰撞计算过程需要遍历模型所有边与障碍物之间的位置关系，导致计算复杂度偏高；

由于圆形构型几何元素简单，所以计算复杂度低，但是机器人轮廓边界与圆形的间隙偏大且极不均匀，因此贴合紧凑一般，均匀性较差； 

复合构型的碰撞计算仅需考虑一条直线段与障碍物之间的距离是否超过叠加的圆形直径，因此碰撞检测计算成本较低，同时该构型两侧与机器人轮廓贴合均匀，紧凑性较好。

因此，复合构型的紧凑性与计算复杂度均介于多边形类型和圆形类型之间。 

表 2.1 总结了外轮廓为矩形的机器人的不同等效模型构型的分析结果，综合对比可知，选择紧凑性、均匀性和计算复杂度均适中的复合构型作为图 2.1中机器人在运动规划中的等效几何模型。

 结合表 2.1分析可以看出，我们很多ROS机器人的底盘就是圆形或者近似圆形的形状，这也是有考虑了几何模型的复杂度。

-模型设计优化-

选择复合构型作为机器人的等效几何模型，综合考虑机器人外轮廓尺寸及其相关约束条件，优化求解最佳模型参数。

3.1 设计目标

复合构型以贴合紧凑、均匀为目标。如图 3.1，该模型由直线段和圆合成，基于直线段向外“膨胀”圆直径的距离，因此定义为膨胀线模型(IFL, inflation line footprint)，表示为

 

 式中，LIFL和CIFL分别表示IFL模型的直线段部分与圆形部分，"⨁" 表示闵可夫斯基和运算。 

IFL模型前后、左右对称，且与机器人矩形外轮廓对称轴线重合，两侧贴合均匀，因此使用IFL与机器人轮廓的面积比近似表示紧凑性，面积比越小，紧凑性越好，表示为

 

 式中，SILF(·)表示面积比，lIFL和dIFL是优化变量，分别表示IFL模型中直线段长度及圆形直径，lM和wM分别表示机器人的外轮廓长、宽。

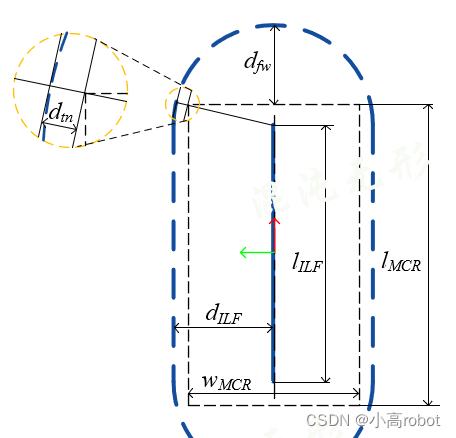
图 3.1 IFL模型

3.2 约束条件

1）包含条件：IFL需要完全包含机器人的外轮廓边界，即ILF模型长度不低于机器人轮廓的长，ILF的圆形部分直径dIFL不能小于机器人宽度的一半，且保证ILF模型与机器人轮廓之间的最小距离（图 3.1 中虚线放大区域）不低于设定值。

式中，dfw表示前、后端最大防碰撞距离，dtn表示ILF模型与机器人轮廓之间的最小距离。

2）防碰撞安全条件：综合分析机器人直行、转弯的最大速度、制动加速度，即前、后端防碰撞距离dfw不低于最大线速度与最大线加速度条件下的制动距离，同理，转向防碰撞距离dtn不低于最大角速度与最大角加速度条件下的制动距离。

 

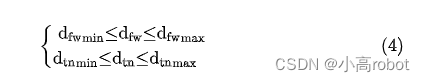
式中，dfwmin、dfwmax分别表示前、后端防碰撞距离的最小值、最大值，dtnmin、dtnmax分别表示转向防碰撞距离的最小值、最大值。 

3）优化变量几何约束条件：ILF模型优化变量范围受限于机器人轮廓约束，lIFL不超过机器人长度，圆形膨胀直径dIFL不小于机器人长度的一半，以限制优化变量范围。

 

式中，dIFLmax表示设定的圆形膨胀直径最大值。

3.3 数值计算

综合式（1-5）得到IFL模型的数学模型，采用设定精度下遍历优化量的方式计算目标函数值，并取其最小值，优化初值及边界为： 

a）机器人边界尺寸为：lM=1085mm，wM=616mm

b）IFL前/后端防碰撞距离极值为：dfwmin=100mm，dfwmax=1000mm

c）IFL转向防碰撞距离极值为：dtnmin=165mm, dtnmax=600mm

d）IFL圆形膨胀直径最大值为：dIFLmax=600mm 遍历计算结果如图 3.2所示，图 3.2（a）为面积比云图，呈单增趋势，红色点表示最小面积比，面积比值为2.41，图 3.2（b）为红点对应的最优IFL模型，图 3.2（c）为对应的实际三维模型，证明了IFL模型应用于机器人具有紧凑性、均匀性等优势。最终计算结果为：lIFL=82.20cm，dIFL=50.08cm。

IFL作为机器人的等效几何模型，被用于运动规划模型中碰撞检测等计算，并将直线段LIFL作为为IFL模型的主轴向量，其方向从机器人后端指向前端，长度不变。 

上述算法对应的源代码放在了《IFL模型优化算法源代码》，具体网页链接： 

https://mianbaoduo.com/o/bread/YpuXmp9x

（a）IFL优化面积比 

 （b）IFL模型结果

 （c）IFL模型应用(URDF)效果图 

 3.2 IFL优化结果

-结论与展望-

本文详细阐述了机器人等效几何模型优化设计的必要性及思路，并以car-like robot为例，从紧凑型、均匀性及复杂度等方面综合对比分析了5种不同等效模型构型的优缺点及适用对象，并介绍了基于IFL模型的设计及优化过程，最终通过数值遍历方法计算得到真实机器人的等效几何模型参数。

<完>