非线性优化 (曲线拟合) 问题：高斯牛顿、g2o 方法总结

最新推荐文章于 2024-05-29 13:25:29 发布

他人是一面镜子，保持谦虚的态度

最新推荐文章于 2024-05-29 13:25:29 发布

阅读量2.4k

点赞数

分类专栏：视觉SLAM基础理论

本文链接：https://blog.csdn.net/hltt3838/article/details/105329410

版权

视觉SLAM基础理论专栏收录该内容

50 篇文章 92 订阅

订阅专栏

其实还有一个Ceres库可以进行优化，但是之前的博客已经具体分析了，所以这里就对其余两个进行了介绍，相关的内容是SLAM14讲里面的知识

一、理论部分

我们先用一个简单的例子来说明如何求解最小二乘问题，然后展示如何手写高斯牛顿法和优化库求解此问题

高斯牛顿法

g2o曲线拟合

g2o （General Graphic Optimization ， G 2 O ）。它是一个基于图优化的库。图优化是一种将非线性优化与图论结合起来的理论，因此在使用它之前，我们花一点篇幅介绍一个图优化理论。

图优化理论简介我们已经介绍了非线性最小二乘的求解方式。它们是由很多个误差项之和组成的。然而，仅有一组优化变量和许多个误差项，我们并不清楚它们之间的关联。比方说，某一个优化变量 x j 存在于多少个误差项里呢？我们能保证对它的优化是有意义的吗？进一步，我们希望能够直观地看到该优化问题长什么样。于是，就说到了图优化。图优化，是把优化问题表现成图（ Graph ）的一种方式。这里的图是图论意义上的图。一个图由若干个顶点（ Vertex ），以及连接着这些节点的边（ Edge ）组成。进而，用顶点表示优化变量，用边表示误差项。于是，对任意一个上述形式的非线性最小二乘问题，我们可以构建与之对应的一个图。

图 6-2 是一个简单的图优化例子。我们用三角形表示相机位姿节点，用圆形表示路标点，它们构成了图优化的顶点；同时，蓝色线表示相机的运动模型，红色虚线表示观测模型，它们构成了图优化的边。此时，虽然整个问题的数学形式仍是式（6.12 ）那样，但现在我们可以直观地看到问题的结构了。如果我们希望，也可以做去掉孤立顶点或优先优化边数较多（或按图论的术语，度数较大）的顶点这样的改进。但是最基本的图优化，是用图模型来表达一个非线性最小二乘的优化问题。而我们可以利用图模型的某些性质，做更好的优化。 g2o 为 SLAM 提供了图优化所需的内容。下面我们来演示一下 g2o 的使用方法。

g2o 的编译与安装

在使用一个库之前，我们需要对它进行编译和安装。读者应该已经体验很多次这个过程了，它们基本都是大同小异的。关于 g2o ，读者可以从 github 下载它： https://github. com/RainerKuemmerle/g2o，或从本书提供的第三方代码库中获得。

解压代码包后，你会看到 g2o 库的所有源码，它也是一个 CMake 工程。我们先来安装它的依赖项（部分依赖项与 Ceres 有重合）：

sudo apt-get install libqt4-dev qt4-qmake libqglviewer-dev libsuitesparse-dev libcxsparse3.1.2

libcholmod-dev

然后，按照 cmake 的方式对 g2o 进行编译安装即可，我们略去该过程的说明。安装完成后，g2o 的头文件将在 /usr/local/g2o 下，库文件在 /usr/local/lib/ 下。现在，我们重新考虑 Ceres 例程中的曲线拟合实验，在 g2o 中实验一遍。

使用 g2o 拟合曲线

为了使用 g2o ，首先要做的是将曲线拟合问题抽象成图优化。这个过程中，只要记住节点为优化变量，边为误差项即可。因此，曲线拟合的图优化问题可以画成图 6-3 的形式。

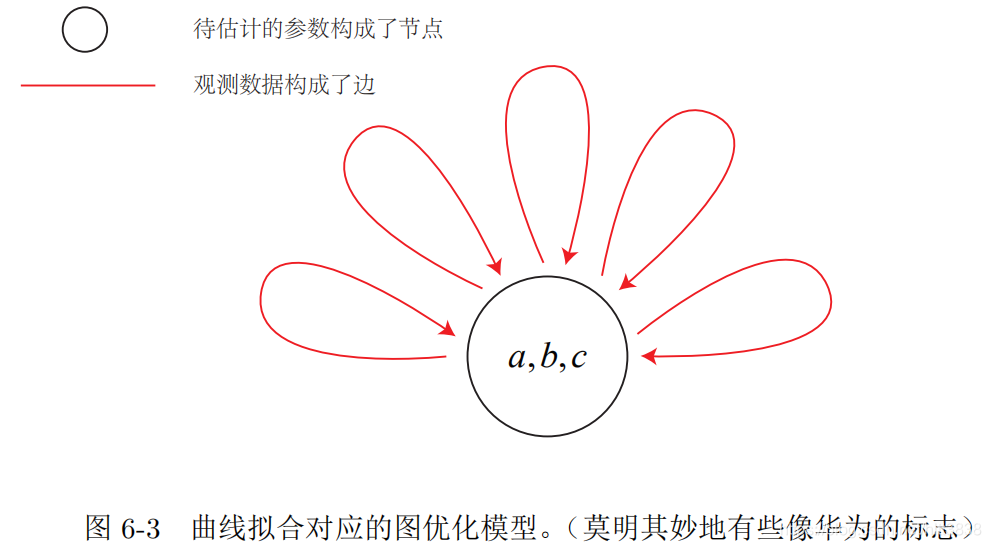
在曲线拟合问题中，整个问题只有一个顶点：曲线模型的参数 a, b, c ；而每个带噪声的数据点，构成了一个个误差项，也就是图优化的边。但这里的边与我们平时想的边不太一样，它们是一元边（ Unary Edge ），即只连接一个顶点 ——因为我们整个图只有一个顶点。所以在图 6-3 中，我们就只能把它画成自己连到自己的样子了。事实上，图优化中一条边可以连接一个、两个或多个顶点，这主要反映在每个误差与多少个优化变量有关。在稍微有些玄妙的说法中，我们把它叫做超边（ Hyper Edge ），整个图叫做超图（ Hyper Graph ） ①。弄清了这个图模型之后，接下来就是在 g2o 中建立该模型，进行优化了。作为 g2o 的用户，我们要做的事主要有以下几个步骤：

1. 定义顶点和边的类型；

2. 构建图；

3. 选择优化算法；

4. 调用 g2o 进行优化，返回结果。

二、实践部分

2.1 手写高斯牛顿法

#include <iostream>
#include <chrono>
#include <opencv2/opencv.hpp>
#include <Eigen/Core>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main(int argc, char **argv) {
  double ar = 1.0, br = 2.0, cr = 1.0;         // 真实参数值
  double ae = 2.0, be = -1.0, ce = 5.0;        // 估计参数值
  int N = 100;                                 // 数据点
  double w_sigma = 1.0;                        // 噪声Sigma值
  double inv_sigma = 1.0 / w_sigma;
  cv::RNG rng;                                 // OpenCV随机数产生器

  vector<double> x_data, y_data;      // 数据
  for (int i = 0; i < N; i++) {
    double x = i / 100.0;
    x_data.push_back(x);
    y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
  }

  // 开始Gauss-Newton迭代
  int iterations = 100;    // 迭代次数
  double cost = 0, lastCost = 0;  // 本次迭代的cost和上一次迭代的cost

  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  for (int iter = 0; iter < iterations; iter++) {

    Matrix3d H = Matrix3d::Zero();             // Hessian = J^T W^{-1} J in Gauss-Newton
    Vector3d b = Vector3d::Zero();             // bias
    cost = 0;

    for (int i = 0; i < N; i++) {
      double xi = x_data[i], yi = y_data[i];  // 第i个数据点
      double error = yi - exp(ae * xi * xi + be * xi + ce);
      Vector3d J; // 雅可比矩阵
      J[0] = -xi * xi * exp(ae * xi * xi + be * xi + ce);  // de/da
      J[1] = -xi * exp(ae * xi * xi + be * xi + ce);  // de/db
      J[2] = -exp(ae * xi * xi + be * xi + ce);  // de/dc

      H += inv_sigma * inv_sigma * J * J.transpose();
      b += -inv_sigma * inv_sigma * error * J;

      cost += error * error;
    }

    // 求解线性方程 Hx=b
    Vector3d dx = H.ldlt().solve(b);
    if (isnan(dx[0])) {
      cout << "result is nan!" << endl;
      break;
    }

    if (iter > 0 && cost >= lastCost) {
      cout << "cost: " << cost << ">= last cost: " << lastCost << ", break." << endl;
      break;
    }

    ae += dx[0];
    be += dx[1];
    ce += dx[2];

    lastCost = cost;

    cout << "total cost: " << cost << ", \t\tupdate: " << dx.transpose() <<
         "\t\testimated params: " << ae << "," << be << "," << ce << endl;
  }

  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "solve time cost = " << time_used.count() << " seconds. " << endl;

  cout << "estimated abc = " << ae << ", " << be << ", " << ce << endl;
  return 0;
}

其结果如下，经过多次迭代，曲线拟合趋于收敛的状态！

2.2 使用g2o进行曲线拟合

#include <iostream>
#include <g2o/core/g2o_core_api.h>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/core/optimization_algorithm_dogleg.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <Eigen/Core>
#include <opencv2/core/core.hpp>
#include <cmath>
#include <chrono>

using namespace std;

// 曲线模型的顶点，模板参数：优化变量维度和数据类型
class CurveFittingVertex : public g2o::BaseVertex<3, Eigen::Vector3d> {
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW

  // 重置
  virtual void setToOriginImpl() override {
    _estimate << 0, 0, 0;
  }

  // 更新
  virtual void oplusImpl(const double *update) override {
    _estimate += Eigen::Vector3d(update);
  }

  // 存盘和读盘：留空
  virtual bool read(istream &in) {}

  virtual bool write(ostream &out) const {}
};

// 误差模型 模板参数：观测值维度，类型，连接顶点类型
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW

  CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}

  // 计算曲线模型误差
  virtual void computeError() override {
    const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
    const Eigen::Vector3d abc = v->estimate();
    _error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
  }

  // 计算雅可比矩阵
  virtual void linearizeOplus() override {
    const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
    const Eigen::Vector3d abc = v->estimate();
    double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
    _jacobianOplusXi[0] = -_x * _x * y;
    _jacobianOplusXi[1] = -_x * y;
    _jacobianOplusXi[2] = -y;
  }

  virtual bool read(istream &in) {}

  virtual bool write(ostream &out) const {}

public:
  double _x;  // x 值， y 值为 _measurement
};

int main(int argc, char **argv) {
  double ar = 1.0, br = 2.0, cr = 1.0;         // 真实参数值
  double ae = 2.0, be = -1.0, ce = 5.0;        // 估计参数值
  int N = 100;                                 // 数据点
  double w_sigma = 1.0;                        // 噪声Sigma值
  double inv_sigma = 1.0 / w_sigma;
  cv::RNG rng;                                 // OpenCV随机数产生器

  vector<double> x_data, y_data;      // 数据
  for (int i = 0; i < N; i++) {
    double x = i / 100.0;
    x_data.push_back(x);
    y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
  }

  // 构建图优化，先设定g2o
  typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType;  // 每个误差项优化变量维度为3，误差值维度为1
  typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型

  // 梯度下降方法，可以从GN, LM, DogLeg 中选
  auto solver = new g2o::OptimizationAlgorithmGaussNewton(
    g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
  g2o::SparseOptimizer optimizer;     // 图模型
  optimizer.setAlgorithm(solver);   // 设置求解器
  optimizer.setVerbose(true);       // 打开调试输出

  // 往图中增加顶点
  CurveFittingVertex *v = new CurveFittingVertex();
  v->setEstimate(Eigen::Vector3d(ae, be, ce));
  v->setId(0);
  optimizer.addVertex(v);

  // 往图中增加边
  for (int i = 0; i < N; i++) {
    CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
    edge->setId(i);
    edge->setVertex(0, v);                // 设置连接的顶点
    edge->setMeasurement(y_data[i]);      // 观测数值
    edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma)); // 信息矩阵：协方差矩阵之逆
    optimizer.addEdge(edge);
  }

  // 执行优化
  cout << "start optimization" << endl;
  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  optimizer.initializeOptimization();
  optimizer.optimize(10);
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "solve time cost = " << time_used.count() << " seconds. " << endl;

  // 输出优化值
  Eigen::Vector3d abc_estimate = v->estimate();
  cout << "estimated model: " << abc_estimate.transpose() << endl;

  return 0;
}

在这个程序中，我们从 g2o 派生出了用于曲线拟合的图优化顶点和边： CurveFittingVertex 和 CurveFittingEdge ，这实质上是扩展了 g2o 的使用方式。在这两个派生类中，我们重写了重要的虚函数：

1. 顶点的更新函数：oplusImpl 。

我们知道优化过程最重要的是增量 ∆ x 的计算，而该函数处理的是 x k +1 = x k + ∆ x 的过程。

读者会觉得这并不是什么值得一提的事情，因为仅仅是个简单的加法而已，为什么 g2o 不帮我们完成呢？在曲线拟合过程中，由于优化变量（曲线参数）本身位于向量空间中，这个更新计算确实就是简单的加法。但是，当优化变量不处于向量空间中时，

比方说 x 是相机位姿，它本身不一定有加法运算。这时，就需要重新定义增量如何加到现有的估计上的行为了。按照第四讲的解释，我们可能使用左乘更新或右乘更新，而不是直接的加法。

2. 顶点的重置函数： setToOriginImpl 。这是平凡的，我们把估计值置零即可。

3. 边的误差计算函数： computeError 。该函数需要取出边所连接的顶点的当前估计值，根据曲线模型，与它的观测值进行比较。这和最小二乘问题中的误差模型是一致的。

4. 存盘和读盘函数： read, write 。由于我们并不想进行读写操作，就留空了。定义了顶点和边之后，我们在 main 函数里声明了一个图模型，然后按照生成的噪声数据，往图模型中添加顶点和边，最后调用优化函数进行优化。g2o 会给出优化的结果：

三、小结

本节介绍了 SLAM 中经常碰到的一种非线性优化问题：由许多个误差项平方和组成的最小二乘问题。我们介绍了它的定义和求解，并且讨论了两种主要的梯度下降方式：GaussNewton 和 Levenberg-Marquardt 。在实践部分中，我们分别使用了 Ceres 和 g2o 两种优化库求解同一个曲线拟合问题，发现它们给出了相似的结果。由于我们还没有详细谈 Bundle Adjustment ，所以实践部分选择了曲线拟合这样一个简单但有代表性的例子，以演示一般的非线性最小二乘求解方式。特别地，如果用 g2o 来拟合曲线，我们必须先把问题转换为图优化，定义新的顶点和边，这种做法是有一些迂回的——g2o 的主要目的并不在此。相比之下，Ceres 定义误差项，求曲线拟合问题则自然了很多，因为它本身即是一个优化库。然而，在 SLAM 中，更多的问题是，一个带有许多个相机位姿和许多个空间点的优化问题如何求解。特别地，当相机位姿以李代数表示时，误差项关于相机位姿的导数如何计算，将是一件值得详细讨论的事。我们将在后续的章节中发现，g2o 提供了大量的顶点和边的类型，使得它在相机位姿估计问题中非常方便。而在Ceres 中，我们不得不自己实现每一个 Cost Function，带来了一些不便。在实践部分的两个程序中，我们没有去计算曲线模型关于三个参数的导数，而是利用了优化库的数值求导，这使得理论和代码都会简洁一些。Ceres 库提供了基于模板元的自动求导和运行时的数值求导，而 g2o 只提供了运行时数值求导这一种方式。但是，对于大多数问题，如果我们能够推导出雅可比矩阵的解析形式并告诉优化库，就可以避免数值求导中的诸多问题。最后，希望读者能够适应 Ceres 和 g2o 这些大量使用模板编程的方式。也许一开始会看上去比较吓人（特别是 Ceres 设置 Problem 和 g2o 初始化部分的代码），但是一旦熟悉

之后，就会觉得这样的方式是自然的，而且容易扩展。我们将在 SLAM 后端章节中，继续讨论稀疏性、核函数、位姿图（Pose Graph ）等问题。

他人是一面镜子，保持谦虚的态度

关注

0
点赞
踩
9

收藏

觉得还不错? 一键收藏
打赏
2
评论
非线性优化 (曲线拟合) 问题：高斯牛顿、g2o 方法总结

一、g2o图优化（General Graph Optimization）g2o最基本的类结构是怎么样的呢？我们如何来表达一个Graph，选择求解器呢？我们祭出一张图：先看上半部分。SparseOptimizer 是我们最终要维护的东东。它是一个Optimizable Graph，从而也是一个Hyper Graph。一个 SparseOptimizer 含有很多个顶点（都继承自 Bas...
复制链接

扫一扫