1.背景
最近看到一篇TIE文章，七月底才被接受的。
感觉论文的方法很好，我感觉这应该是目前最好的电流环性能了（无超调且以最快的速度达到参考值，而且不依赖参数）。下面就是论文中的实验波形，c1、c2、c3就是论文提出的方法。
2.研究背景概述
下面这部分内容是我结合论文的综述部分，以及我之前做过的各种电流环得到的总结。
由于和电机控制性能密切相关的是电机的电磁转矩，而电磁转矩由电流环控制，因此，电流环的动稳态性能直接决定着伺服电机的控制性能。
与现有的各种电流环控制方法相比，无差拍预测电流控制（Deadbeat predictive current control，DPCC）在PMSM电流控制的动态和稳态过程中均表现出良好的性能。
特别是动态性能方面，在模型参数精确、电压足够的条件下，DPCC可以保证实际电流经过两个控制周期即可达到所需参考电流，且此过程中不会出现电流超调[1]。这意味着DPCC在所有电流控制方案中，具有最高的控制带宽。
然而，DPCC唯一的不足是严重依赖电机参数，当控制器中的电机参数与实际电机参数不匹配时，DPCC的动稳态性能都将大幅下降。因此，如何提高DPCC方案的鲁棒性，以保证DPCC高效的动稳态性能，成为了当下的研究热点。
无差拍预测电流控制的研究现状
2.1基于观测器的无差拍预测电流控制的研究现状
为了进一步消除参数失配的影响，近年来基于超局部模型的DPCC方法得到广泛研究[2]-[4]，其中电流控制器基于超局部模型而不是PMSM模型设计。超局部模型只有控制器比例增益和扰动观测增益两个增益需要设置。值得注意的是，超局部模型的控制器比例增益设置为电感的倒数时，将使系统具有更优越的性能；同时超局部模型将PMSM的反电势和电阻压降等效为扰动，利用观测器对扰动进行观测，因此超局部模型相当于降低了对电阻、反电势参数的依赖性。
在文献[2]中，扰动项采用扩张状态观测器（extended state observer，ESO）估计，而控制器比例增益直接设置为电感的倒数，这表明该方法仍然依赖于PMSM的电感参数。为了进一步改进，在文献[3]中提出了一种有效的无参数超局部模型的DPCC方法，其中使用有限时间梯度方法估计电感的倒数，并使用ESO估计扰动项。在文献[4]中，提出了具有基于参数估计器的ESO的无模型DPCC，以同时估计模型增益和干扰项。文献[3]和[4]中的方法不需要电机参数，然而，扰动项的观测速度仍然受到扰动观测器带宽的限制。在动态过程中，由于扰动项是不断变化的，且观测器无法立刻完成扰动项的无偏估计，因此基于观测器的强鲁棒DPCC难以实现理想DPCC的高动态性能。
为实现理想DPCC的高动态性能，电机参数是不可或缺的。
就比如我直接做了高阶ESO的对比，虽然高阶ESO可以提高电流环的动态性能；但是当电机出现电感失配的，高阶ESO就会引入非常多的高频噪声，性能就变得很差。
https://zhuanlan.zhihu.com/p/716635704
https://zhuanlan.zhihu.com/p/716635704
2.2基于电机参数辨识的无差拍预测电流控制的研究现状
2.2.1基于信号注入的参数辨识方法现状
不同于避免使用电机参数的方法，另一种增强鲁棒性的解决方案是通过在线参数估计获得准确的机器参数[5]，[6]。在[5]中，基于具有电流注入的干扰观测器的重构特征向量，估计DPCC的定子电阻和电感。在[6]中，将具有高频电流注入的全参数估计方法与DPCC相结合以提高性能。在文献[5]和[6]中，由于电压方程个数有限，同时估计dq电感、电阻、磁链参数会导致方程缺秩问题，因此信号注入对于多参数估计是必要的。但是，信号注入会引起副作用，例如增加铜损和增大转矩脉动，在一定程度上会影响电机稳态性能。而且，基于信号注入的方法同样立刻完成对电机参数的无偏估计，此类方法需要电机在运行时具有一定的稳态时间。
文献[6]就是我之前复现的无差拍参数辨识。虽然辨识的效果非常好，但是时间稍微有点长了。因此基于信号注入的参数辨识方法并不适用于转速、负载频繁变化的伺服电机系统。
https://zhuanlan.zhihu.com/p/687206417https://zhuanlan.zhihu.com/p/687206417
2.2.2基于误差纠正的参数辨识方法现状
在基于ESO的无参数超局部模型的DPCC方法中（即文献[2]提出的方法），当系统出现参数失配时，ESO观测的扰动数值不为零，反之亦然。根据此原理，在最新的文献[7][8]中，基于误差纠正的参数辨识方法被提出，其原理为，根据ESO观测的扰动数值，不断调节纠正控制器估计的电机参数，直至ESO观测的扰动数值为零。ESO观测的扰动数值为零，这意味着控制器估计的电机参数与实际电机参数完全一致，整个控制系统不存在参数偏差，即可实现理想DPCC的高动态性能。文献[7]和[8]提出的基于误差纠正的参数辨识方法，可以在动态和稳态过程中对参数进行辨识，恰特别适用于工况频繁变化的伺服场合。
文献[7]就是我之前做的自适应增益ESO，它主要是辨识了电感参数，大大提升了传统无模型预测控制的鲁棒性。
https://zhuanlan.zhihu.com/p/696436558
文献[8]就是我今天要复现的这一篇。
文章的主要创新点就是，不需要信号注入，即可实现电机电感、电阻、磁链三个参数的辨识；得到这三个电机参数之后，就可以保证了DPCC的鲁棒性，进而实现无超调的，快速的动态性能。
3.参考文献
[1] Q. Zhang, Y. Fan and C. Mao, "A Gain Design Method for a Linear Extended State Observers to Improve Robustness of Deadbeat Control," in IEEE Transactions on Energy Conversion, vol. 35, no. 4, pp. 2231-2239, Dec. 2020.
[2] Y. Zhang, J. Jin and L. Huang, "Model-Free Predictive Current Control of PMSM Drives Based on Extended State Observer Using Ultralocal Model," in IEEE Transactions on Industrial Electronics, vol. 68, no. 2, pp. 993-1003, Feb. 2021.
[3] J. Chen, Y. Fan, M. Cheng, Q. Zhang and Q. Chen, "Parameter-Free Ultralocal Model-Based Deadbeat Predictive Current Control for PMVMs Using Finite-Time Gradient Method," in IEEE Transactions on Industrial Electronics, vol. 70, no. 6, pp. 5549-5559, June 2023.
[4] X. Yuan, Y. Zuo, Y. Fan and C. H. T. Lee, "Model-Free Predictive Current Control of SPMSM Drives Using Extended State Observer," in IEEE Transactions on Industrial Electronics, vol. 69, no. 7, pp. 6540-6550, July 2022.
[5] Y. Yao, Y. Huang, F. Peng, J. Dong and H. Zhang, "An Improved Deadbeat Predictive Current Control With Online Parameter Identification for Surface-Mounted PMSMs," in IEEE Transactions on Industrial Electronics, vol. 67, no. 12, pp. 10145-10155, Dec. 2020.
[6] Y. Wang et al., "A Robust DPCC for IPMSM Based on a Full Parameter Identification Method," in IEEE Transactions on Industrial Electronics, vol. 70, no. 8, pp. 7695-7705, Aug. 2023.
[7] X. Wu, J. Kang, M. Yang, T. Wu and S. Huang, "Model-Free Deadbeat Predictive Current Control for SPMSM Based on Adaptive Gain Extended State Observer," in IEEE Transactions on Transportation Electrification.
[8] F. Wang, W. Kong and R. Qu, "Model Parameter Self-Correcting Deadbeat Predictive Current Control for SPMSM Drives," in IEEE Transactions on Industrial Electronics.
4.文章复现及一些注意事项
文章的具体内容我就不说了。有兴趣就翻翻文章来看看。
其主要思路就是，根据预测电流的误差，进行参数辨识。这一特点，其实在我前面复现的两篇文章中也有使用。
https://zhuanlan.zhihu.com/p/696436558https://zhuanlan.zhihu.com/p/696436558
https://zhuanlan.zhihu.com/p/701200054https://zhuanlan.zhihu.com/p/701200054
但是前面这两篇文章的缺点在于，不能同时辨识电感、电阻、磁链三个参数。
这是因为电机的电压方程只有两个，而电感、电阻、磁链三个参数相当于三个未知数，所以是求解不了的。这个问题也就是方程的缺秩问题。
为了解决方程的缺秩问题，这篇文章用不同工况下的电机数据构成新的电机方程。如下图所示，下图展示了文章辨识电阻和磁链的流程图。其主要思路就是通过判断两个周期的情况下的电流差值是否足够大，如果电流差值足够大，相当于电机处于两个不同的工况，进而记录这个两个工况下的预测误差数据、电流数据、转速数据，然后利用最小二乘法recursive least squares (RLS)进行辨识。
4.1注意事项1——控制方程的搭建
文章写的电机方程都是矢量形式，但是搭建方程都是需要按照标量方程来搭建的，如果不会矢量方程和标量方程转化的话，可以看我下面这篇知乎，里面放了一个链接。
https://zhuanlan.zhihu.com/p/682880365https://zhuanlan.zhihu.com/p/682880365
4.2注意事项2——RLS公式
文章中给了最小二乘法的公式和参考文献。但是我在参考文献[22]中并没有找到这篇参考文献。
而且论文中给的最小二乘法的公式是错误的。我画线的地方，不应该是转置矩阵，而是求逆矩阵。
下面是我找的一篇硕士论文，画线的部分应该是求逆矩阵才对。
此外，最小二乘法的P矩阵，论文中没有告诉怎么取初值。论文中公式（38）L矩阵的初值可以全为0，但是P矩阵不可以全为0。必须取非零数。
但是我发现P矩阵如果取全1的，也是不行的。
4.3注意事项3——参数选取
论文中还构建了两个PI去观测参数。这两个PI的参数配置，直接按照论文里给的数据就好了。虽然文章的参数很多，但是论文基本都给了具体数值。
4.4注意事项4——复现流程
我的搭建步骤如下：
（1）按照论文中的DPCC-ESO公式，先搭建DPCC-ESO。
（2）增加d轴的PI模块，d轴的PI模块也就是电感辨识模块。搭建好这个电感辨识模块之后可以先看看电感辨识的是否准确。准确了再搭建别的模块。
（3）增加q轴的PI模块，q轴的PI模块是用于估计论文中的辅助变量。由于论文中已经给了辅助变量的表达式，所以可以计算看看搭建的PI模块输出的辅助变量数值是否正确。
（4）最后搭建最小二乘法的电阻、磁链辨识模块。
5.仿真展示
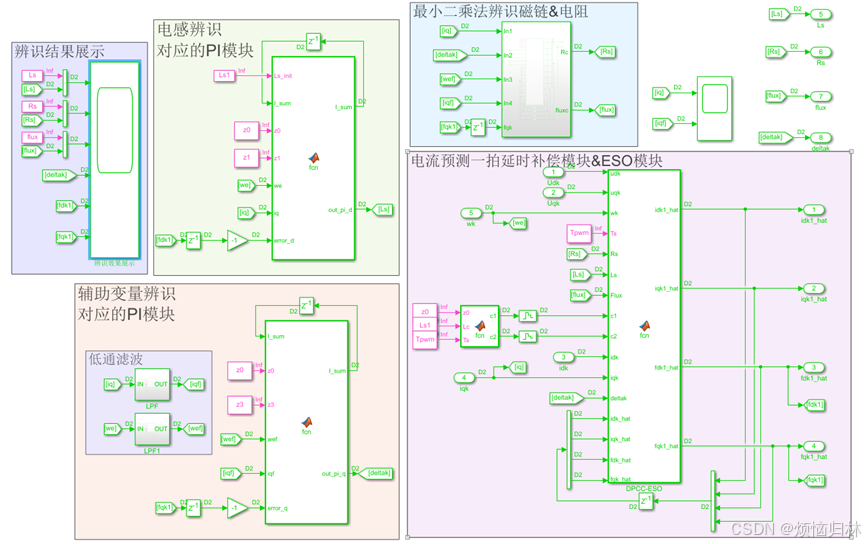
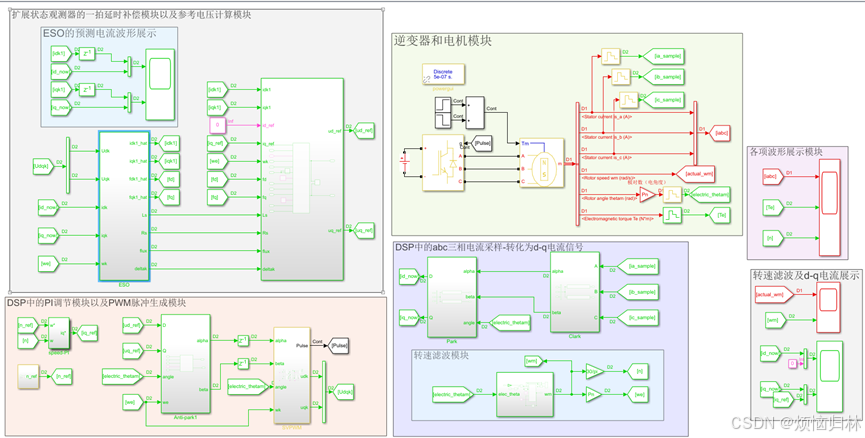
为了验证这个算法的优越性，我这里用两台参数不同的电机。
5.1仿真电机1
5.1.1参数设定
Ts = 5e-7;%仿真步长
Tpwm = 1e-4;%开关周期
Tspeed = 1e-4;%转速采样周期
Vdc = 350;%直流母线电压
Tdead = 0e-6;%死区时间
%下面这是电机的实际参数
Pn = 4;%电机极对数
Ls = 8.5e-3;%定子电感，采用隐极的，Ld=Lq=Ls
Rs = 1;%定子电阻
flux = 0.1688;%永磁体磁链
iqmax = 20;%额定电流
J = 4e-3;%转动惯量
B = 2e-3;%阻尼系数
n_init = 500;%初始转速
fc_lpf = 500;%转速计算的低通滤波器截止频率
%转速环PI参数
Kpw=0.25;
Kiw=50;
%ESO参数
z0 = 0.85;
z1 = 0.99;
z3 = 0.99;
lanbuda = 0.98;
%这是DSP内部的控制器参数
Ls1 = 2*Ls;%电感参数设置为实际电感的两倍
Ld1 = Ls1;
Lq1 = Ls1;
Rs1 = 0*Rs;%电阻参数设置为0
flux1 = 2*flux;%磁链参数设置为实际磁链的两倍
5.1.2仿真工况
速度参考设置如下（包含正弦参考速度以及阶跃指令）：
转矩指令也设定为阶跃信号。
5.1.3整体波形展示
可以看到，在负载、转速变化的情况，整体波形都较好，转速、电流超调小。
5.1.4参数辨识情况
可以看到，在转速、转速正弦变化的情况下，这个方法也可以有效辨识电感、电阻、磁链三个参数。而且辨识的结果基本与真实值完全一致。
5.1.5电流跟踪情况
可以看到，实际电流完美跟踪参考电流。0s附近的出现电流波动是因为此时电机参数还未完成辨识；0.5以及0.7s的电流波动，都是由于直流母线电压不足。
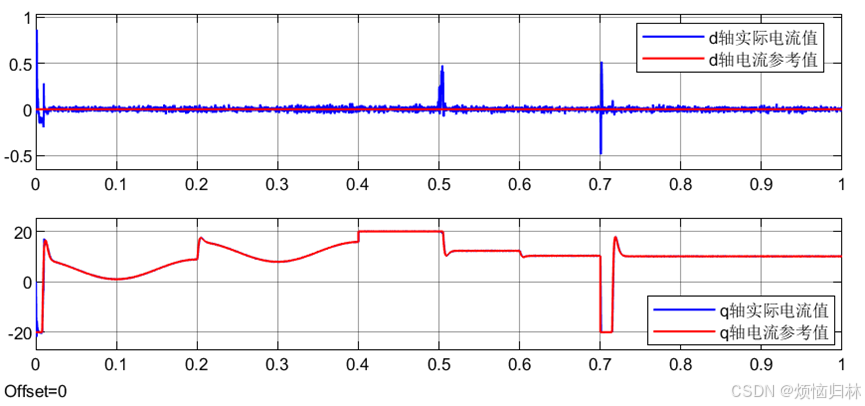
我下面这里把0.7s处电流响应放大。可以看到这个q轴电流的响应速度非常快，而且q轴电流达到参考电流时，没有出现超调或者响应速度减慢的情况。
下面对比一下无参数辨识的DPCC-ESO和传统DPCC的情况。可以看到，这篇论文方法的性能远超无参数辨识的DPCC-ESO、和传统DPCC。
5.2仿真电机2
5.2.1参数设定
Ts = 5e-7;%仿真步长
Tpwm = 1e-4;%开关周期
Tspeed = 1e-4;%转速采样周期
Vdc = 310;%直流母线电压
Tdead = 0e-6;%死区时间
%下面这是电机的实际参数
Pn = 4;%电机极对数
Ls = 3e-3;%定子电感，采用隐极的，Ld=Lq=Ls
Rs = 1.2;%定子电阻
flux = 0.1194;%永磁体磁链
iqmax = 4*sqrt(2)*1.3;%最大电流我设置为额定电流的1.3倍
J = 1.1e-3;%转动惯量
B = 1e-4;%阻尼系数
n_init = 1000;%初始转速
fc_lpf = 500;%转速计算的低通滤波器截止频率
%转速环PI参数
Kpw=0.25;
Kiw=50;
%ESO参数
z0 = 0.9;
z1 = 0.996;
z3 = 0.996;
lanbuda = 0.98;
%这是DSP内部的控制器参数
Ls1 = 2*Ls;%电感参数设置为实际电感的2倍
Ld1 = Ls1;
Lq1 = Ls1;
Rs1 = 0*Rs;%电阻参数设置为0
flux1 = 2*flux;%磁链参数设置为实际磁链的2倍
5.2.2整体波形展示
可以看到，在负载、转速变化的情况，整体波形都较好，转速、电流超调小。
5.2.3参数辨识情况
可以看到，在转速、转速正弦变化的情况下，这个方法也可以有效辨识电感、电阻、磁链三个参数。而且辨识的结果基本与真实值完全一致。
为什么我的电感辨识脉动有点大？主要是这里涉及PI参数，我把PI增益调大了。而论文中的PI增益很小。如果把PI增益调小，那么这个方法辨识的速度就慢了。我懒得跑太久的仿真，所以就把增益设置的比较大了。
5.2.4电流跟踪情况
可以看到，实际电流完美跟踪参考电流。
下面是0.7s处的电流放大图。0.7s左右时，参数已经完成辨识，所以这时候q轴电流动态响应极快，而且无超调。
5.3总结
上述方法在两台参数不同的电机上，都有非常好的效果。都能够实现以最快速达到参考电流且无超调的控制性能。
扫一扫
1513
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
