通信原理板块——截短循环码、BCH码、RS码

微信公众号上线，搜索公众号小灰灰的FPGA,关注可获取相关源码，定期更新有关FPGA的项目以及开源项目源码，包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

1、截短循环码(truncated cyclic code)
设计纠错编码方案，信息位数k、码长n和纠错能力都是预先给定的。
采用将码长截短的方法，得到满足需求的编码。
设给定一个(n,k)循环码，共有2^k
种码组，使其前i(0<i<k)个信息位全为“0”，变成仅有2^(k-i)种码组，从中删去这i位全“0”的信息位，最终得到一个(n-i,k-i)的线性码。即为截短循环码。
截短循环码与截短前的循环码至少具有相同的纠错能力，且截短循环码的编解码方法仍和截短前的方法一样。
2、BCH码
BCH码是一种获得广泛应用的能够纠正多个错码的循环码。
BCH码解决了生成多项式与纠错能力的关系，可以在给定纠错能力要求的条件下，寻找码的生成多项式。
BCH码分为两类，即本原BCH码和非本原BCH码
①本原BCH码
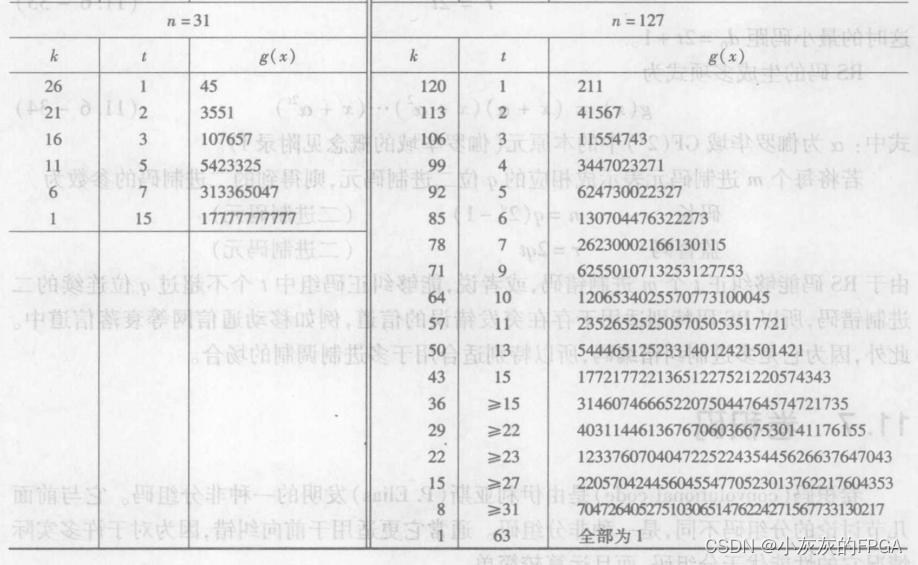
本原BCH码的生成多项式g(x)中含有最高次数为m的本原多项式，且码长为n=(2^m-1),其中m≥3,为正整数
BCH码的码长n与监督位、纠错个数t之间的关系
对于正整数m(m≥3)和正整数t(t<m/2)，必定存在一个码长为n=(2^m-1),监督位为n-k≤mt，能纠正所有不多于t个随机错误的BCH码
通过查找表可获取生成多项式g(x)，生成多项式系数是用八进制数字列出的


②非本原BCH码
本原BCH码的生成多项式g(x)中不含有最高次数为m的本原多项式，且码长为n，是(2^(m-1))
的一个因子，码长n一定除得尽(2^m-1)

③扩展BCH码
BCH码的长度都为奇数，为了得到偶数长度的BCH码，并增大检错能力，在BCH码生成多项式中乘上一个因式(x+1)，得到扩展BCH码(n+1,k)
扩展BCH码相当于在原BCH码上增加一个校验位，码距比原BCH码增加1，不再具有循环性。
3、RS码
RS码是一类具有很强纠错能力的多进制BCH码
对于m进制的RS码的码长为n=m-1=2^q-1,其中q≥2，为整数
对于能够纠正t个错误的RS码，监督码元数目为r=2t，最小码距为d0=2t+1
RS码的生成多项式为g(x)=(x+α)×(x+α^2)
……(x+α^(2t))
其中α为伽罗华域GF(2^q)中的本原元
RS码适用于存在突发错误的信道，比如移动通信网等衰落信道中。
也适用于多进制调制场合，因为是多进制纠错编码。