参考博主carsim如何获得轮胎侧偏刚度_SSW.hani的博客-CSDN博客_轮胎侧偏刚度计算公式
以B级车为例:
魔术公式轮胎模型:
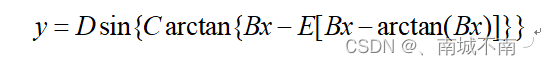
1、打开B级车的轮胎界面。

2、打开EXCEL表格。

3、第一行数据为垂直载荷,寻找与参考垂直载荷相近的一列数据,将其(除开第一行数据)保存于新建的EXCEL表格中,同时将第一列数据也进行保存,并命名为“R15”。

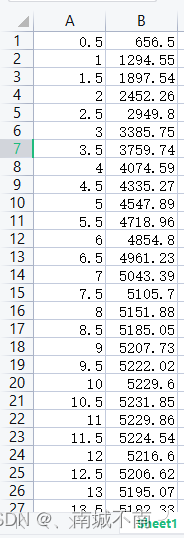
4、打开matlab,导入数据。


5、在matlab命令行窗口输入如下代码:(获取数据)
x=R15(:,1);
y=R15(:,2);

6、打开曲线拟合工具。

7、输入公式:d*sin(c*atan(b*x-e*(b*x-atan(b*x))))

8、设置参数,使拟合曲线逼近。

9、可见,曲线拟合效果不错,记录数据。B=0.1169;C=2.161;D=5233。

10、计算侧偏刚度。
kf=kr=BCD=0.1169*2.161*5233=1322N/°=75783N/rad。
























 431
431

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








