基于飞机配电优化负荷管理系统研究（Matlab代码实现）

最新推荐文章于 2025-05-06 13:51:16 发布

然哥依旧

最新推荐文章于 2025-05-06 13:51:16 发布

阅读量949

点赞数 26

文章标签： matlab 开发语言

本文链接：https://blog.csdn.net/m0_64583023/article/details/147709071

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、文章下载

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

飞机电力系统 (EPS) 是安全关键系统，可为起落架或飞行控制执行器等重要负载提供电力。随着一些液压、气动和机械部件被电气部件取代，现代飞机 EPS 变得越来越复杂，因为硬件子系统数量更多以及它们与嵌入式控制软件的交互 [1]。电力系统的电气化允许实施智能控制技术，通过对电力资源的优化管理来实现更高的性能和整体效率。然而，今天的 EPS 设计主要遵循顺序衍生设计过程，其估计早期设计决策对最终实施的影响的能力有限（最初由德国 DoD1 为国防应用开发的 V 图的变体）。为了降低开发过程中的风险，新开发的设计通常是旧飞机 EPS 的转世，由于当今的飞机需要大量新功能，这种做法注定很快就会停止，我们的方法建立在许多结果的基础上，这些结果为更正式的 EPS 设计方法开辟了道路。在 [4] 中，作者提出了一个通过仿真对飞机子系统进行建模和架构探索的平台。类似地，在 [5] 中，作者利用飞机的飞行动力学模型与驱动系统模型耦合来利用仿真。虽然已经报道了几种用于电力电子、开关和转换器的优化技术，但优化整个配电系统的问题在文献中很少受到关注。在 [6] 中，确定了网络各个点的最佳电压和功率水平，以最小化总重量、安装成本和燃料消耗。在 [7] 中提出了一种遵循 PBD 范式的面向优化的 EPS 设计方法。然而，[6] 和 [7] 的主要关注点是发电机的选择和拓扑的设计，即不同 EPS 组件之间的互连，而不是 EPS 接触器开关逻辑的优化设计和负载管理。在 [8] 中讨论了 EPS 控制协议的正确构造设计的自动化程序。系统规范首先使用线性时序逻辑 [9] 进行转换，然后通过利用形式化方法自动合成以保证安全约束。然而，虽然最终解决方案的正确性得到保证，但它在许多性能指标方面的最优性，例如使用的发电机数量和卸载负载，并没有得到解决。

不同组件之间的连接由单线图 (SLD) 指定，这是一种表示三相电力系统的简化符号 [1]。交流和直流发电机为许多交流和直流负载或电力转换设备（例如变压器和整流器单元）供电。除了连接到飞机发动机的发电机外，发电元件还包括辅助动力装置（APU）和电池。电力通过一条或多条总线分配，发电机与负载的连接通过一系列机电开关（称为接触器）进行布线。一部分负载很关键，无法卸载，而其他负载可以在紧急情况下脱机。最后，电流、电压和接触器传感器用于监控系统状态并识别可能的故障。

本文结构如下。在第 II 节对示例 EPS 系统及其要求进行了简要描述后，第 III 节说明了我们的分层优化负载管理方法，包括问题的优化，而第 IV 节总结了Matlab模拟结果。最后，在第五节中，得出结论。

数学模型

$P_{\mathrm{req}_{j}}(t)=\sum_{i=1}^{n_{j}} c_{j i}(t) L_{j i}^{s}(t)+\sum_{i=n_{j}+1}^{N_{j}} c_{j i}(t) L_{j i}^{n s}(t)$

$S_{o} C_{i}(t+1)=S_{o} C_{i}(t)+T_{s} \cdot K \cdot \beta_{i}(t)$

$\underline{S o C} \leq S o C_{i}(t) \leq \overline{S o C}$

$N o S_{i j}\left(t^{*}\right)=\sum_{t=t^{*}}^{t^{*}+H \cdot T_{s}}\left|\delta_{i j}(t)-\delta_{i j}(t+1)\right|$

详细数学模型及解释见第四部分。

结论

本文讲解了一种用于飞机配电的分层优化负载管理系统。在我们的方法中，高级负载管理系统 (HL-LMS) 通过在后退水平方法中求解有效的混合整数线性程序来协调减载、源分配和电池利用率。最佳控制问题的结果作为建议提供给可以直接驱动 EPS 接触器的低级负载管理系统 (LL-LMS)。每次发生故障时，来自 HL-LMS 的结果可以忽略，LL-LMS 应用预定义的最坏情况控制策略，直到使用实际系统状态更新高级优化问题公式以适应故障。除了保证系统安全外，我们的分层架构在卸载负载百分比和使用源数量方面显示出相对于仅基于 LL-LMS 的传统架构的显着性能改进。最后，仿真结果表明，最优控制问题在所选应用的范围内可以合理地扩展。

📚2 运行结果

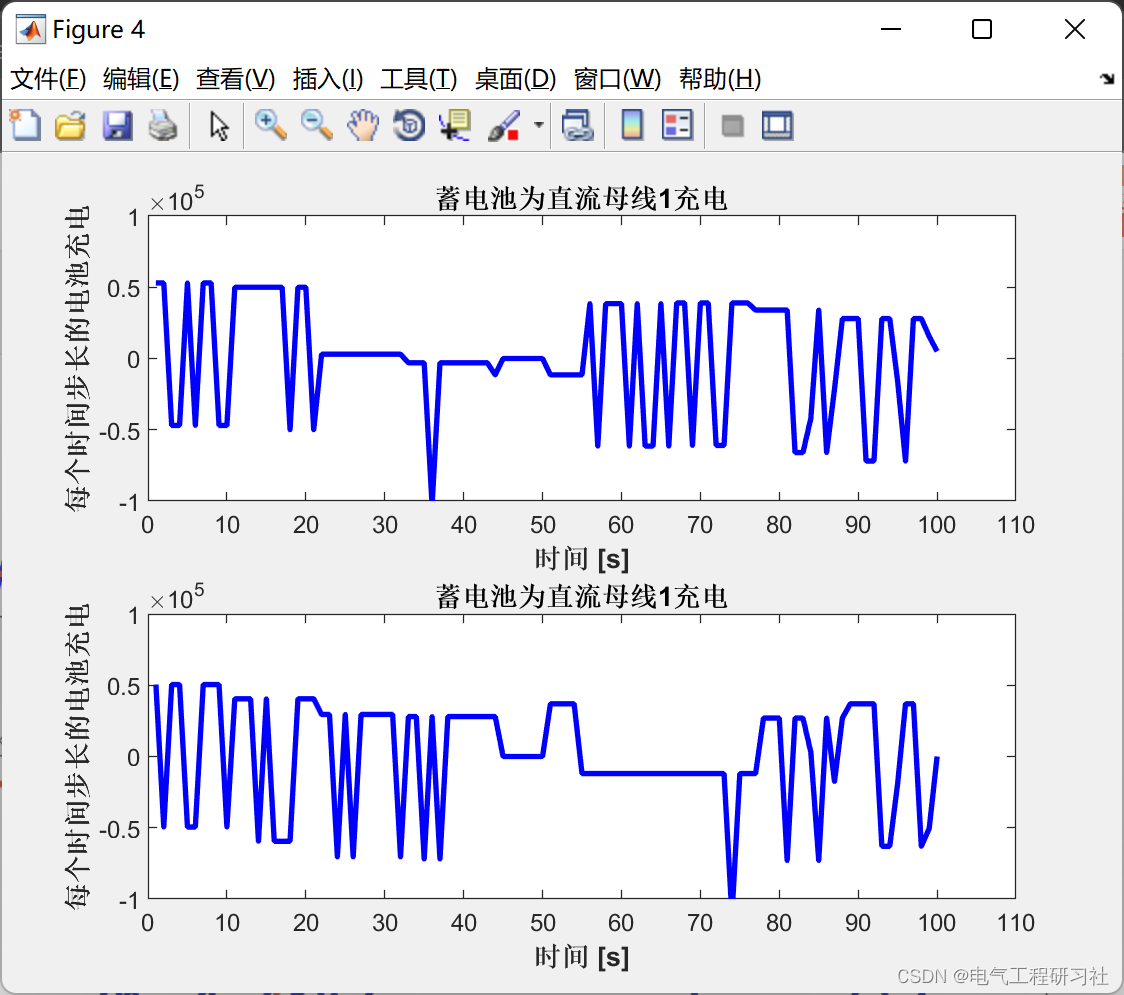
部分代码：

function [configs] = HLLMS(sensors, constants) %only using 'sensors' for generator status
N = constants.N; % number of timesteps (use all timesteps -- no interpolation or kron)
Nt = constants.Nt; % prediction horizon
Nl = constants.Nl; % number of loads connected to each bus
Ns = constants.Ns; % number of power sources
Nb = constants.Nb; % number of HVAC buses

%% load the "loads"
[Ls1 Lns1 Ls2 Lns2] = sliceWorkloads(sensors, constants); %get relevant slice of historicalWorkloads

%% Max. Power supply by Engines and APU
U1=constants.generatorOutput(1); Peng1=U1*ones(1,Nt);
U2=constants.generatorOutput(2); Peng2=U2*ones(1,Nt);
U3=constants.generatorOutput(3); Papu=U3*ones(1,Nt);
U=[U1*ones(1,Nt); U2*ones(1,Nt); U3*ones(1,Nt)];
P=[Peng1' Peng2' Papu'];
startBatteryCharge1=sensors.batteryCharge1; startBatteryCharge2=sensors.batteryCharge2;

%% Optimization problem set-up
tic;
%Coefficients (one set for Bus 1, one set for Bus 2):
Lambda1=[0 1 2]; Lambda2=[1 0 2]; %generator priority table (GR, GL, APU)
%Lambda1=[0 2 0]; Lambda2=[1 2 0]; %pri table: prefer APU over other side's generator
Gamma1=1000*ones(1,Nl); Gamma2=500*ones(1,Nl); %load shedding priority table (one value for each load at each timestep)
M=3; %'mu' -- weight for alpha (see eq.9 in OLMS paper)
%M=1;

% Decision variables (one set for Bus 1, one set for Bus 2)
C1=binvar(Nl,Nt,'full'); C2=binvar(Nl,Nt,'full'); %C1(l,t) = "shed load l at time t?:
Del1=binvar(Ns,Nt,'full'); Del2=binvar(Ns,Nt,'full'); %Del1(g,t) = "is bus 1 powered by generator g at time t?"
Beta1=sdpvar(1,Nt,'full'); Beta2=sdpvar(1,Nt,'full'); %Beta1(1,t) = "amount of pwr used for battery 1 at time t"
Y1=sdpvar(Ns,Nt,'full'); Y2=sdpvar(Ns,Nt,'full'); %what is this?
alpha=binvar(Nt,Ns,'full'); %alpha(t,g) = "is anything drawing pwr from generator g at time t?"
Pito1=sdpvar(Nt,Ns,'full'); Pito2=sdpvar(Nt,Ns,'full'); %Pito1(t,g) = "amount of pwr delivered by generator g to bus 1 at time t"
BETA1 = sdpvar(1,Nt,'full'); BETA2 = sdpvar(1,Nt,'full'); %cumulative battery charge. (lowercase Beta is per-timestep change in charge)
nSwitch1 = sdpvar(1,Nt,'full'); nSwitch2 = sdpvar(1,Nt,'full'); nSwitch3 = sdpvar(1,Nt,'full'); nSwitch4 = sdpvar(1,Nt,'full'); nSwitch5 = sdpvar(1,Nt,'full'); nSwitch6 = sdpvar(1,Nt,'full');

% Constraints
cons=[];
%cons=[cons, 0 <= BETA1, 0 <= BETA2];
cons=[cons, 0 <= BETA1 <= constants.maxBatteryLevel, 0 <= BETA2 <= constants.maxBatteryLevel]; %battery charge level can't be negative
for i=1:Nl-1
cons=[cons, C1(i,:) <= C1(i+1,:), C2(i,:) <= C2(i+1,:)];
end
cons=[ cons, sum(Del1,1) == ones(1,Nt)]; % \delta_11(t) + \delta12(t) + \delta_13(t)=1 \forall t>=0
cons=[ cons, sum(Del2,1) == ones(1,Nt)];
for i=1:Ns %hard code "generator broken" where necessary
if (sensors.genStatus(i) == 0)
cons=[cons, alpha(:,i)==0]; %require that generator i is off
cons=[cons, Del1(i,:)==0, Del2(i,:)==0]; %require that nobody draws power from gen i
end
end

x=1:1:N;
xi=0:N/(Nt-1):N; xi(1)=1; % 0:10:100

% the following five lead to MILP.
cons=[cons, sum(C1.*interp1(x,Ls1',xi)',1) + sum(interp1(x,Lns1',xi),2)' == sum(Y1,1) - Beta1]; %\sum cji(t)*lji(t)= \sum \deta_ji *P_source_i - Betaj
cons=[cons, sum(C2.*interp1(x,Ls2',xi)',1) + sum(interp1(x,Lns2',xi),2)' == sum(Y2,1) - Beta2];
cons=[cons, Y1' + Y2' == alpha.*P]; % The three constraints of the form \delta_{11}*P_{1to1} + \delta_{2to1}*P_{2to2}=P_{eng1}
cons=[cons, 0 <= Y1 <= Pito1', 0 <= Y2 <= Pito2'];
cons=[cons, Pito1' - U.*(1-Del1) <= Y1 <= U.*Del1, Pito2' - U.*(1-Del2) <= Y2 <= U.*Del2];

if(sensors.time >= constants.tMinBatteryLevel)
cons=[cons, constants.minBatteryLevel <= BETA1, constants.minBatteryLevel <= BETA2];
display(sprintf('using minBatteryLevel starting at time %d', sensors.time))
elseif((constants.tMinBatteryLevel - sensors.time) < 0) %TODO: check correctness
display('not using minBatteryLevel constraint')
my_tMinBatteryLevel = constants.tMinBatteryLevel - sensors.time;
cons=[cons, maxBatteryLevel <= BETA1(my_tMinBatteryLevel:Nt) >= minBatteryLevel, BETA2(my_tMinBatteryLevel:Nt) >= minBatteryLevel]; %enforce lower bound on battery charge level after the tMinBatteryLevel-th timestep
end

%everything is shifted to start at 2 (see 'configs' below), so Beta1(1),Beta2(1) is (ignored?)
BETA1(1) = startBatteryCharge1; BETA2(1) = startBatteryCharge2;
for i=2:Nt
cons=[cons, BETA1(i) == BETA1(i-1) + Beta1(i), BETA2(i) == BETA2(i-1) + Beta2(i)];
end

nSwitch1=0; nSwitch2=0; nSwitch3=0; nSwitch4=0; nSwitch5=0; nSwitch6=0;
for i=1:Nt-1
nSwitch1=nSwitch1 + abs( Del1(1,i)-Del1(1,i+1) );
nSwitch2=nSwitch2 + abs( Del1(2,i)-Del1(2,i+1) );
nSwitch3=nSwitch3 + abs( Del1(3,i)-Del1(3,i+1) );

nSwitch4=nSwitch4 + abs( Del2(1,i)-Del2(1,i+1) );
nSwitch5=nSwitch5 + abs( Del2(2,i)-Del2(2,i+1) );
nSwitch6=nSwitch6 + abs( Del2(3,i)-Del2(3,i+1) );
end
NOAS=3; % Number Of Allowed Switchings
cons=[cons, nSwitch1<=NOAS, nSwitch2<=NOAS, nSwitch3<=NOAS];
cons=[cons, nSwitch4<=NOAS, nSwitch5<=NOAS, nSwitch6<=NOAS];

% Objective
obj=0;
obj = obj + sum(Gamma1 * (1-C1)) + sum (Gamma2 * (1-C2));
obj = obj + sum(Lambda1 * Del1) + sum(Lambda2 * Del2);
obj = obj + M * sum(sum(alpha));

options=sdpsettings('solver','Cplex'); %windows needs 'Cplex' and mac is ok with 'cplex' or 'Cplex'
solvesdp(cons,obj,options);
toc;

Shedding1 = double(C1(:,:));
Shedding2 = double(C2(:,:));
batteryUpdate1 = double(Beta1(:,:));
batteryUpdate2 = double(Beta2(:,:));
Del1_double = double(Del1(:,:));
Del2_double = double(Del2(:,:));
GeneratorOnOff = double(alpha(:,:)); % unlike the other variables, alpha's time index comes first

configs = []; %array of 'config' data structures
for i=1:(Nt-1) %1 to horizon
BusGen = [0 0];
[myMax BusGen(1)] = max(Del1_double(:,i+1)); %BusGen(1) is argmax here
[myMax BusGen(2)] = max(Del2_double(:,i+1));

config = struct('Shedding1', Shedding1(:,i+1)', 'Shedding2', Shedding2(:,i+1)', 'BusGen', BusGen, 'batteryUpdate1', batteryUpdate1(:,i+1), 'batteryUpdate2', batteryUpdate2(:,i+1), 'GeneratorOnOff', GeneratorOnOff(i,:), 'HLadviceUsed', true);
configs = [configs config];
end
end

function [Ls1 Lns1 Ls2 Lns2] = sliceWorkloads(sensors, constants)
nTimestepsOuterLoop = max(size(constants.historicalWorkloads.Ls1(1,:)));
lo = sensors.time;
hi = min((sensors.time + constants.N)-1, nTimestepsOuterLoop); %out-of-bounds check
Ls1 = constants.historicalWorkloads.Ls1(:, lo:hi);
Lns1 = constants.historicalWorkloads.Lns1(:, lo:hi);
Ls2 = constants.historicalWorkloads.Ls2(:, lo:hi);
Lns2 = constants.historicalWorkloads.Lns2(:, lo:hi);
end