Eigen矩阵的平移,旋转,缩放

最新推荐文章于 2025-06-10 15:59:04 发布

master cat

最新推荐文章于 2025-06-10 15:59:04 发布

阅读量374

点赞数 1

分类专栏：数学文章标签：矩阵线性代数

本文链接：https://blog.csdn.net/mankeywang/article/details/139863322

版权

数学专栏收录该内容

2 篇文章

订阅专栏

#include <Eigen/Core>
#include <Eigen/Dense>

平移

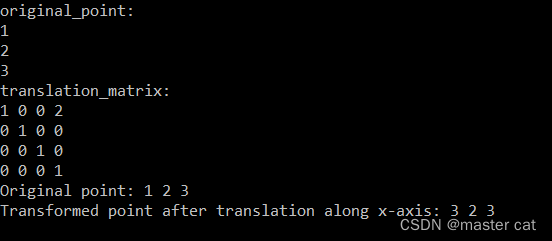
x轴

	// 原始点或对象的坐标
	Eigen::Vector3d original_point(1.0, 2.0, 3.0);
	std::cout << "original_point: " << std::endl << original_point << std::endl;
	
	// x 轴上的平移量
	double tx = 2.0;
	// 构造平移矩阵
	Eigen::Matrix4d translation_matrix = Eigen::Matrix4d::Identity();
	translation_matrix(0, 3) = tx;
	std::cout << "translation_matrix: " << std::endl << translation_matrix << std::endl;
	// 1 0 0 2
	// 0 1 0 0
	// 0 0 1 0
	// 0 0 0 1

	// 应用平移变换
	Eigen::Vector4d homogenous_point(original_point.x(), original_point.y(), original_point.z(), 1.0);
	Eigen::Vector4d transformed_point = translation_matrix * homogenous_point;

	std::cout << "Transformed point after translation along x-axis: " << transformed_point.transpose().block<1, 3>(0, 0) << std::endl;

在这里插入图片描述

y轴

	// 原始点或对象的坐标
	Eigen::Vector3d original_point(1.0, 2.0, 3.0);

	// y 轴上的平移量
	double ty = -1.0;

	// 构造平移矩阵
	Eigen::Matrix4d translation_matrix = Eigen::Matrix4d::Identity();
	translation_matrix(1, 3) = ty;
	std::cout << "translation_matrix: " << std::endl << translation_matrix << std::endl;
	// 1  0  0   0
	// 0  1  0  -1
	// 0  0  1   0
	// 0  0  0   1

	// 应用平移变换
	Eigen::Vector4d homogenous_point(original_point.x(), original_point.y(), original_point.z(), 1.0);
	Eigen::Vector4d transformed_point = translation_matrix * homogenous_point;
	// 输出结果
	std::cout << "Original point: " << original_point.transpose() << std::endl;
	std::cout << "Transformed point after translation along y-axis: " << transformed_point.transpose().block<1, 3>(0, 0) << std::endl;

在这里插入图片描述

z轴

	// 原始点或对象的坐标
	Eigen::Vector3d original_point(1.0, 2.0, 3.0);

	// z 轴上的平移量
	double tz = 0.5;

	// 构造平移矩阵
	Eigen::Matrix4d translation_matrix = Eigen::Matrix4d::Identity();
	translation_matrix(2, 3) = tz;
	std::cout << "translation_matrix: " << std::endl << translation_matrix << std::endl;
	// 1   0   0   0
	// 0   1   0   0
	// 0   0   1  0.5
	// 0   0   0   1

	// 应用平移变换
	Eigen::Vector4d homogenous_point(original_point.x(), original_point.y(), original_point.z(), 1.0);
	Eigen::Vector4d transformed_point = translation_matrix * homogenous_point;
	// 输出结果
	std::cout << "Original point: " << original_point.transpose() << std::endl;
	std::cout << "Transformed point after translation along y-axis: " << transformed_point.transpose().block<1, 3>(0, 0) << std::endl;

在这里插入图片描述

旋转

x轴

	#define M_PI 3.14159265358979323846
	// 原始点或对象的坐标
	Eigen::Vector3d original_point(0.0, 1.0, 0.0);

	// 绕 x 轴顺时针旋转角度（弧度）
	double angle = M_PI / 4.0; // 45 度
	 绕 x 轴逆时针旋转角度（弧度）
	//double angle = -M_PI / 4.0; // -45 度

	// 构造旋转矩阵
	Eigen::Matrix3d rotation_matrix;
	rotation_matrix = Eigen::AngleAxisd(angle, Eigen::Vector3d::UnitX());

	// 应用旋转变换
	Eigen::Vector3d rotated_point = rotation_matrix * original_point;

	// 输出结果
	std::cout << "Original point: " << original_point.transpose() << std::endl;
	std::cout << "Rotated point after clockwise rotation around x-axis: " << rotated_point.transpose() << std::endl;

y轴

	#define M_PI 3.14159265358979323846
	// 原始点或对象的坐标
	Eigen::Vector3d original_point(0.0, 1.0, 0.0);

	 绕 y 轴顺时针旋转角度（弧度）
	//double angle = M_PI / 3.0; // 60 度
	// 绕 y 轴逆时针旋转角度（弧度）
	double angle = -M_PI / 3.0; // -60 度

	// 构造旋转矩阵
	Eigen::Matrix3d rotation_matrix;
	rotation_matrix = Eigen::AngleAxisd(angle, Eigen::Vector3d::UnitY());

	// 应用旋转变换
	Eigen::Vector3d rotated_point = rotation_matrix * original_point;

	// 输出结果
	std::cout << "Original point: " << original_point.transpose() << std::endl;
	std::cout << "Rotated point after clockwise rotation around y-axis: " << rotated_point.transpose() << std::endl;

z轴

	#define M_PI 3.14159265358979323846
	
	// 原始点或对象的坐标
	Eigen::Vector3d original_point(0.0, 1.0, 0.0);

	 绕 z 轴顺时针旋转角度（弧度）
	//double angle = M_PI / 6.0; // 30 度

	// 绕 z 轴逆时针旋转角度（弧度）
	double angle = -M_PI / 6.0; // -30 度

	// 构造旋转矩阵
	Eigen::Matrix3d rotation_matrix;
	rotation_matrix = Eigen::AngleAxisd(angle, Eigen::Vector3d::UnitZ());

	// 应用旋转变换
	Eigen::Vector3d rotated_point = rotation_matrix * original_point;

	// 输出结果
	std::cout << "Original point: " << original_point.transpose() << std::endl;
	std::cout << "Rotated point after clockwise rotation around z-axis: " << rotated_point.transpose() << std::endl;