测量误差相关知识(二)

1 什么是测量误差？

对自然界的任何量进行实验和测量时，由于参与测量的5个要素–测量装置(测量仪器)、测量人员、测量方法、测量环境和被测对象自身都不够做到完美无缺，使得测量结果与其真实值之间存在差异，这个差异在数学上叫做测量误差。

任何测量必然会产生误差，不含误差的测量结果是不存在的。

2 误差分析的意义？

• 误差分析能直接应用于科学理论检验。
• 运用误差理论直接对测量结果进行分析研究可能有重大发现

3 误差分析在测量中的作用？

• 误差分析，来源于对测量的认识。不同测量方式，误差分布存在差异，需要选择合适的分析方法。
• 误差分析可以反作用与测量，从中分析问题，改进测量。

4 测量误差分布有哪些？

1)正态分布：当产生误差的因素很多，彼此相互独立，又是均匀的小，其总误差根据中心极限定理接近于正态分布。

2)均匀分布：误差有一确定的范围，在此范围内，误差出现的概率各处相等，又叫矩形分布或等概率分布。

服从均匀分布的情形：

• 数据修约导致的误差
• 数字式测量仪器对示值量化(分辨力)导致的误差
• 测量仪器由于滞后、摩擦效应导致的误差
• 按级使用的数字式仪表、测量仪器最大允许误差导致的误差
• 用上下界给出的线膨胀系数
• 测量仪器度盘或齿轮回差引起的误差
• 平衡指示器凋零不准导致的误差

3)反正弦分布：该随机误差与某一角度成正弦关系。

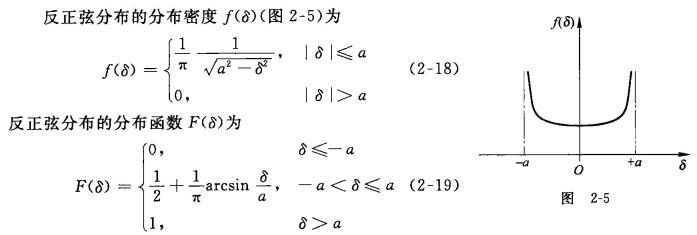
服从该分布的情形：

• 度盘偏心引起的测角误差
• 正弦振动引起的位移误差
• 无线电中失配引起的误差
• 随时间按正余弦变化的温度误差

4)三角形分布：当两个误差限相同且服从均匀分布的随机误差求和时，其和的分布规律服从三角形分布，又称辛普森分布。

三角形分布密度：

服从该分布可能情形：

• 相同修约间隔给出的两独立量之和或差，由修约导致的误差
• 因分辨力引起的两次测量结果之和或差的误差
• 用替代法检定标准电子元件或测量衰减时，凋零不准导致的误差
• 两相同均匀分布的合成

5)其他分布：直角分布、截尾正态分布、双峰正态分布、二点分布、投影分布等。

5 如何判定误差属于哪种分布？

• 物理来源判断发：根据误差产生来源，判断其属于何种类型。
• 函数关系法：利用随机变量的函数关系，判断误差属于何种分布。
• 图形判断法：对重复测量获得的样本数据绘出其测量点列图或频数分布图(确定误差分布，n取50-100；确定分布规律，n取200-1000)，然后根据图形判断它与何种分布最接近。

正态分布的点列图：单峰性、有界性、对称性、抵偿性

均匀分布的点列图：具有有界性、对称性、抵偿性，但不具有单峰性。

6 误差分布的统计检验方法有哪些？

1）直方图法：

• 将误差值出现的区间等距分为若干子区间，误差值落在同一子区间的误差为一组，小区间的长度称为组距。分组个数一般根据子样容量n的大小来决定，但一般分为10~30个组为宜。
• 绘制直方图，根据经验频数（即落入各小区间的误差值个数）来绘制。
  计算子样均值x和子样方差s²，用这些统计量来估计母体的参数，并绘制理论分布密度曲线（通常为正态分布曲线）在同一图上。
• 比较直方图和理论分布密度曲线的符合程度，从而判断误差分布是否服从正态分布。

2）统计检验法：

• χ²检验法：根据样本数据的频数与期望频数（即理论频数）之间的差异来构造χ²统计量，进而检验误差分布是否服从指定的理论分布（如正态分布）。
• 柯尔莫哥洛夫-斯米尔诺夫（Kolmogorov-Smirnov）检验法：通过比较样本数据的累积分布函数与理论分布函数之间的差异来检验误差分布。
• 达戈斯提诺（D’Agostino）检验法：结合了偏度和峰度信息来检验误差分布的正态性。
• 夏皮罗-威尔克（Shapiro-Wilk）检验法：适用于小样本情况下检验误差分布的正态性。
• 偏-峰态系数检验法：通过计算样本数据的偏度和峰度，并与正态分布的偏度和峰度进行比较，从而检验误差分布的正态性。

7 如何度量测量的不可靠性？

由于随机误差的存在，等精度测量列中各个测得值一般皆不相同，它们围绕着该测量列的算术平均值有一定的分散，此分散度说明了测量列中单次测量值的不可靠性，必须用一个数值(标准差)作为其不可靠性的评定标准。

标准差的数值小，该测量列相应小的误差就占优势，任一单次测得值对算术平均值的分散度就小，测量的可靠性就大，即测量精度高；反之，测量精度就低。

标准差不是测量列中任何一个具体测得值的随机误差，其大小只说明在一定条件下等精度测量列随机误差的概率分布情况。

标准差的估计方法：贝塞尔公式法、别捷尔斯法、极差法、最大误差法与最大残差法。

参考：《误差分析与数据处理》