三维旋转矩阵 左乘和右乘分析

突然发现自己被旋转矩阵的左乘右乘给搞糊涂了，查了不少博客还是有点晕，这里自己总结一下：
本文所讨论均是基于右手坐标系，旋转也是以正方向旋转，如图所示：

左乘： 坐标系不动，点动，则左乘。【若绕静坐标系（世界坐标系）旋转，则左乘，也是变换矩阵乘坐标矩阵；】
右乘： 点不动，坐标系动，则右乘。【若是绕动坐标系旋转（自身建立一个坐标系），则右乘，也就是坐标矩阵乘变换矩阵】

由于三维旋转可以分解成分别绕三个轴旋转，然后其实就是二维旋转了。为了方便，这里就使用二维旋转举例。
比如绕z轴旋转 theta 角度；
左乘分析如图所示：

而右乘分析：
则是旋转坐标系；点逆时针旋转了theta角，其实也就是相当于坐标轴也逆时针旋转theta角。如图所示：

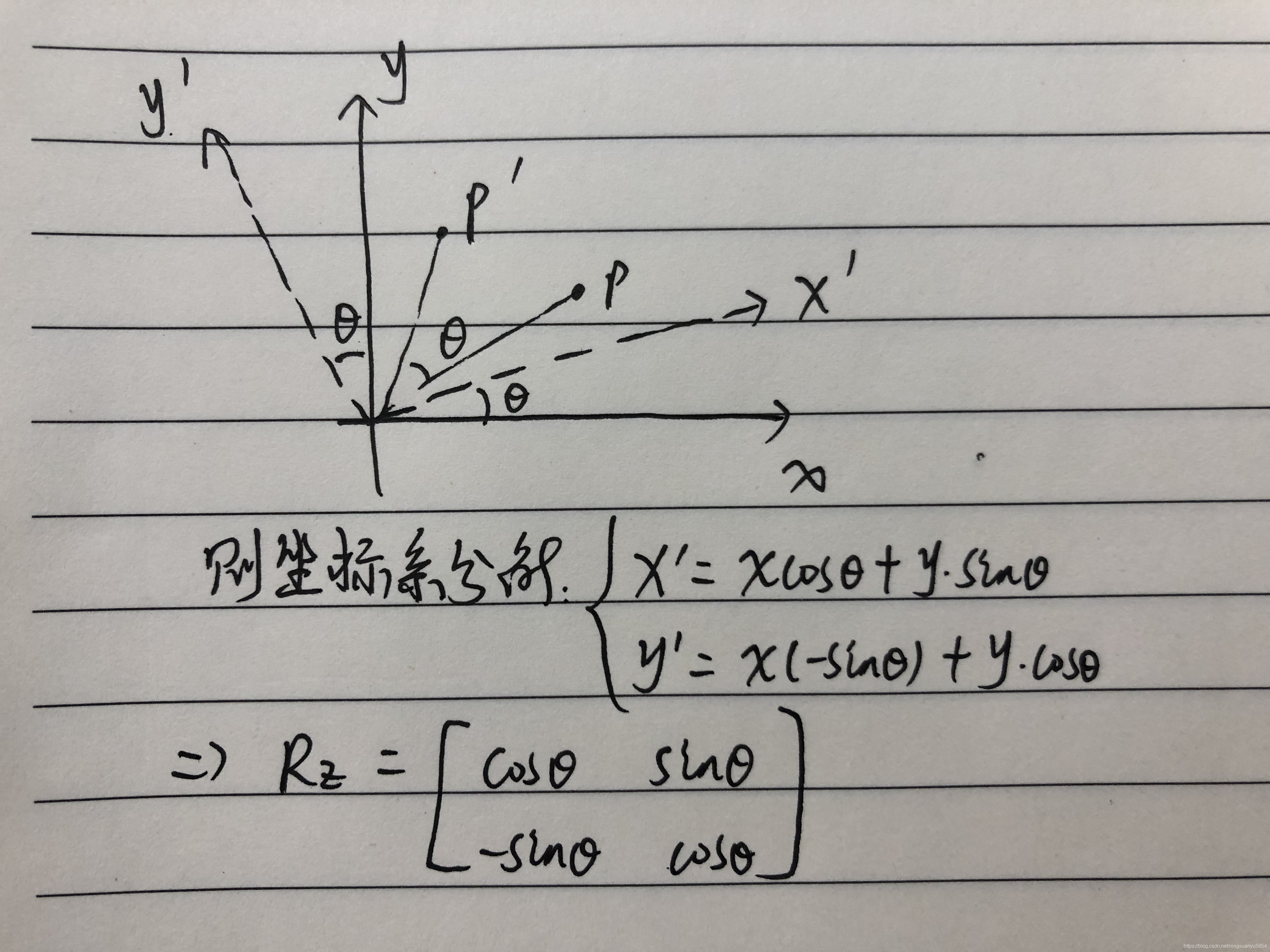
设点原坐标为$[x,y,z]$，旋转后的坐标为$[x^{\prime },y^{\prime },z^{\prime }]$, 设左乘旋转矩阵为$R_{left}$,右乘旋转矩阵为$R_{right}$，
则：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right]=R_{left}\ast \left[\begin{array}{c}x\\ y\\ z\end{array}\right]$$
$$\left[\begin{array}{ccc}{x}^{\prime }& y^{\prime }& z^{\prime }\end{array}\right]=\left[\begin{array}{ccc}x& y& z\end{array}\right]\ast R_{right}$$

观察上面两图计算出来的旋转矩阵还可以得出结论，$R_{left}\ast R_{right}=I$，这意味这这两个矩阵是互为逆。
另外，$R_{left}(\theta )=R_{right}(-\theta )$ 。
【可以说，如果一个旋转矩阵左乘表示逆时针旋转 theta 角，那么将此矩阵右乘的话则表示顺时针旋转 theta 角】
左乘与右乘是可以变换的。也即是说：

$$R_{lef{t}_3}(\theta )\ast R_{lef{t}_2}(\theta )\ast R_{lef{t}_1}(\theta )\ast \left[\begin{array}{c}x\\ y\\ z\end{array}\right]=R_{righ{t}_3}(-\theta )\ast R_{righ{t}_2}(-\theta )\ast R_{righ{t}_1}(-\theta )\ast \left[\begin{array}{c}x\\ y\\ z\end{array}\right]$$

不过建议只是用一种方法来计算旋转矩阵，以免混淆。

【如有错误，欢迎各位批评指正。】

参考博客：https://blog.csdn.net/csxiaoshui/article/details/65446125