用泰勒展开线性化

用泰勒一阶展开线性化

在点附近做泰勒展开：

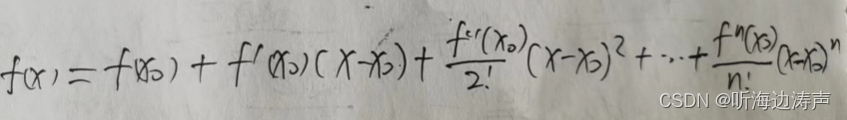
当和很接近的时候，很小，更小，所以可以忽略及后面的高阶项，得到

因为、都是常数，所以等式右边是 x的线性方程，在点附近进行了线性化。

举例

正弦函数线性化

假设

那么做一阶泰勒展开，得到：

如果，即在0点附近做泰勒展开，得

变量的倒数线性化

例如，下面公式：

因为不是线性的，所以公式不是线性的。

现在要在平衡点附件将上面的公式线性化，那么就需要把线性化。

在平衡点和都等于0，带入上式，得

得到平衡点，记该点为，即

记

那么在平衡点附近，做泰勒展开，得

又

将和代入，得

代入公式，得到

化简，得到了在平衡点附近的线性化公式：

二维线性化

下面考虑一个二维的系统 ：

其中是平衡点。

在平衡点附近做一阶泰勒展开：

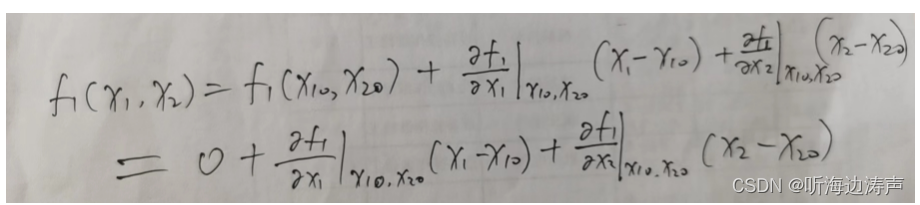
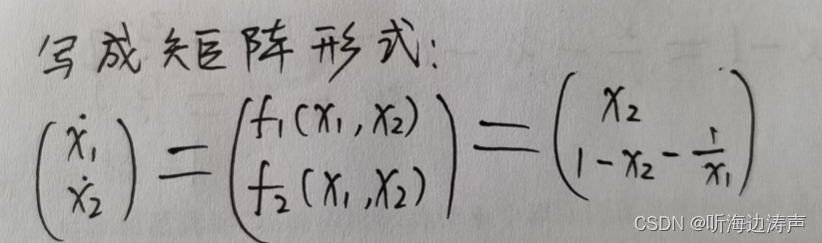
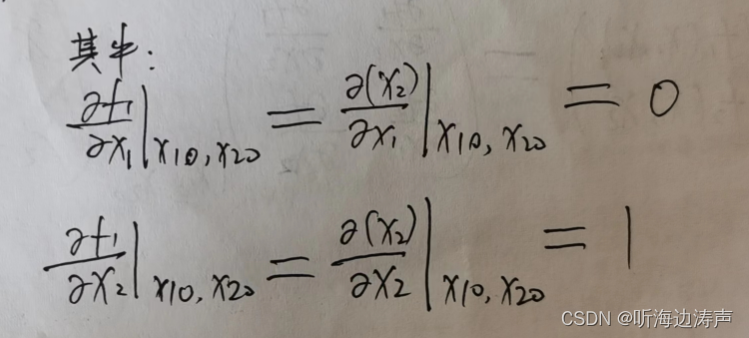
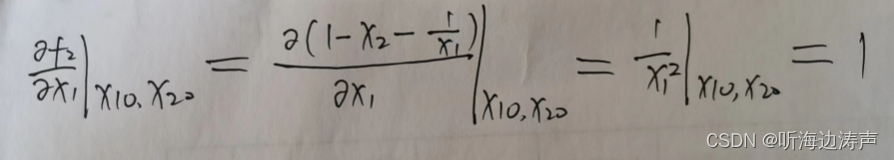
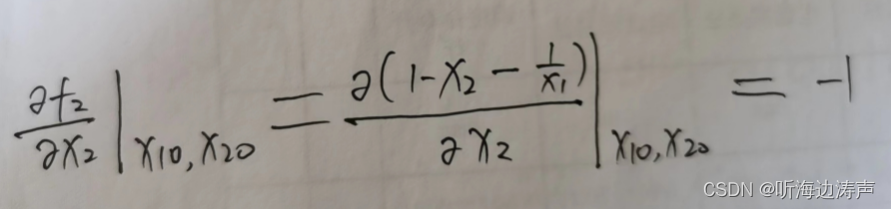
这就完成了二维系统的线性化。

将最开始的变量定义，代入上面第2个公式，转换为一维的公式看看。

开始给出的变量定义：

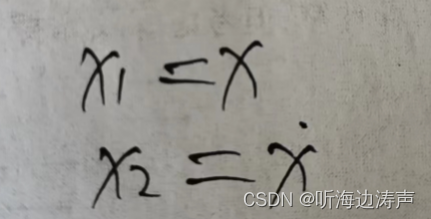
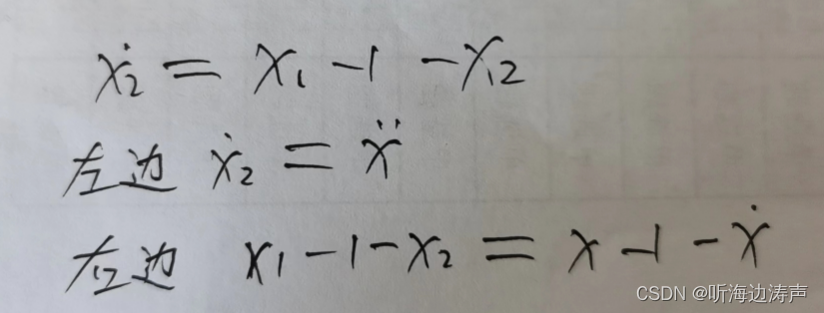
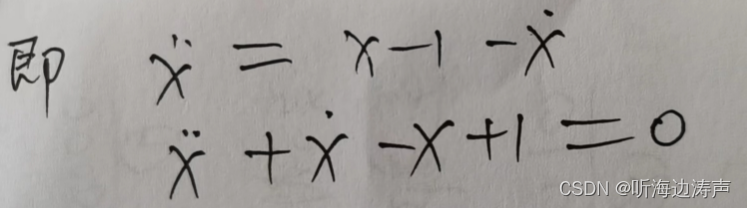
这个线性化的结果和第2个例子用一维给出的线性化结果一样。