【ShaderToy】跳动的心

最新推荐文章于 2024-05-13 10:05:02 发布

pizi0475

最新推荐文章于 2024-05-13 10:05:02 发布

阅读量2.5k

点赞数 2

分类专栏：手机游戏游戏开发游戏引擎 OpenGL ES 图形引擎渲染效果引擎开发 OpenGL Shader

游戏引擎同时被 3 个专栏收录

1659 篇文章 22 订阅

订阅专栏

游戏开发

1649 篇文章 12 订阅

订阅专栏

图形引擎

1623 篇文章 23 订阅

订阅专栏

http://blog.csdn.net/candycat1992/article/details/44040273

写在前面

注：如果你还不了解ShaderToy，请看开篇。

作为ShaderToy系列的第一篇，我们先来点简单的。下面是效果：

（CSDN目前不能传gif文件了，暂时空缺，可以看下面的原shader效果，是一样的）

原Shader地址：https://www.shadertoy.com/view/XsfGRn

代码

我们使用了之前的开篇中的基础模板。这里仅仅给出main函数的代码：

[cpp]view plaincopyprint? 
   
  vec4 main(vec2 fragCoord) {  
     vec2 p = (2.0*fragCoord.xy-iResolution.xy)/min(iResolution.y,iResolution.x);  
   
     p.y -= 0.25;  
       
     // background color  
     vec3 bcol = vec3(1.0,0.8,0.7-0.07*p.y)*(1.0-0.25*length(p));  
       
     // animate  
     float tt = mod(iGlobalTime,1.5)/1.5;  
     float ss = pow(tt,.2)*0.5 + 0.5;  
     ss = 1.0 + ss*0.5*sin(tt*6.2831*3.0 + p.y*0.5)*exp(-tt*4.0);  
     p *= vec2(0.5,1.5) + ss*vec2(0.5,-0.5);  
       
       
     // shape  
     float a = atan(p.x,p.y)/3.141593;  
     float r = length(p);  
     float h = abs(a);  
     float d = (13.0*h - 22.0*h*h + 10.0*h*h*h)/(6.0-5.0*h);  
       
     // color  
     float s = 1.0-0.5*clamp(r/d,0.0,1.0);  
     s = 0.75 + 0.75*p.x;  
     s *= 1.0-0.25*r;  
     s = 0.5 + 0.6*s;  
     s *= 0.5+0.5*pow( 1.0-clamp(r/d, 0.0, 1.0 ), 0.1 );  
     vec3 hcol = vec3(1.0,0.5*r,0.3)*s;  
       
     vec3 col = mix( bcol, hcol, smoothstep( -0.01, 0.01, d-r) );  
       
     return vec4(col,1.0);  
 }  

代码很短，但包含了一些数学公式的计算，不懂的就会觉得很难理解。我们把上面代码拆分成两个部分：背景颜色（bcol），心的颜色（hcol，包含了心的跳动）：

背景颜色

这部分比较简单。这个背景实际上是一个某点为中心，中心最亮、向边缘逐渐变暗的背景，比较常见。但通常我们都是用美术给的纹理直接用，现在我们用纯数学计算来看看如何实现它！

首先，我们在看一个重要变量的计算——p。

[cpp]view plaincopyprint? 
   
 vec2 p = (2.0*fragCoord.xy-iResolution.xy)/min(iResolution.y,iResolution.x);  
   
 .y -= 0.25;  

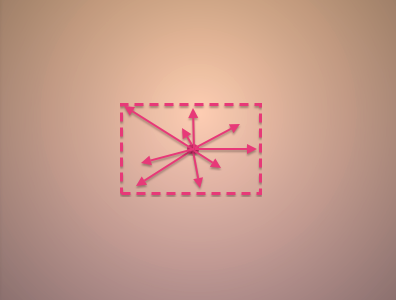
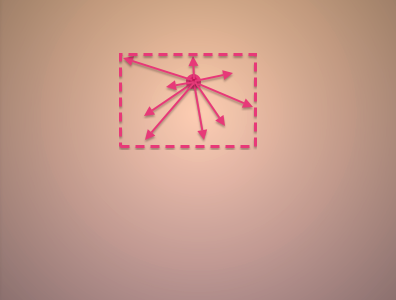
第一行中，代码计算了每一个像素点和屏幕中心点之间的方向向量。我们以图为例说明。

在p.y减去0.25之前，中心点即是屏幕中心，代码先计算了每个像素点到中心的方向（如左图），然后再除以屏幕的高度（或宽度）（如右图）。图例如下：

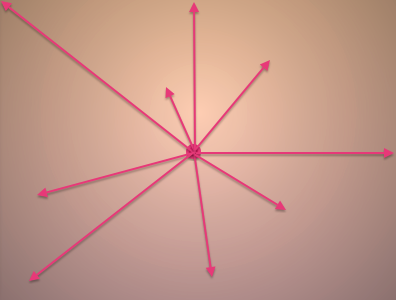
这样的计算结果可以保存每个像素点距离中心的方向、远近等信息。

在这个基础上，我们还可以移动中心点的位置来控制渐变。代码中是将y减去了0.25，即将中心点向上移动了屏幕高度的0.25/2=0.125个单位。

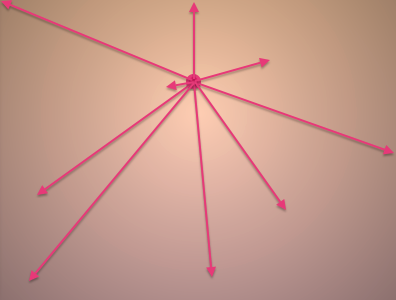
我们可以通过更改代码来看到这样的效果：

[cpp]view plaincopyprint? 
   
 vec3 bcol = vec3(1.0,0.8,0.7-0.07*p.y)*(1.0-length(p));  

[cpp]view plaincopyprint? 
   
 return vec4(bcol,1.0);  

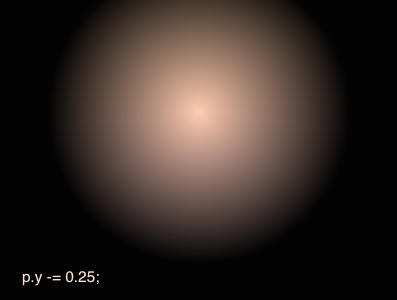
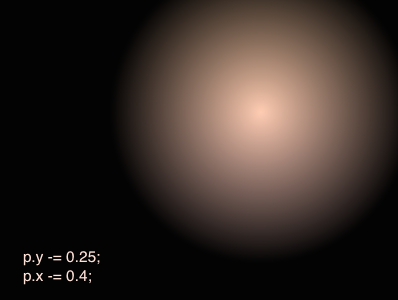
以上步骤即可得到屏幕上每一个点到中心点的方向、相对距离等信息。接下来，我们就可以根据这些信息计算背景颜色了：

[cpp]view plaincopyprint? 
   
 // background color  
 vec3 bcol = vec3(1.0,0.8,0.7-0.07*p.y)*(1.0-0.25*length(p));  

bcol可以认为是一个主背景颜色和像素距离中心点远近值的乘积。其中， (1.0-0.25*length(p)) 是我们对上一步得到的距离进行进一步计算，由于 length(p) 的值可能大于1（如果屏幕x轴大于y轴，那么p的x方向的绝对值有些会大于1；反之，如果屏幕y轴大于x轴，那么p的y方向的绝对值有些会大于1），因此，我们需要在 length ( p ) 的基础上乘以系数0.25。当然，0.25是经验值，我们可以把这个参数做成shader的一个属性，供调节。 vec3(1.0,0.8,0.7-0.07*p.y) 中， vec3 ( 1.0 , 0.8 , 0.7) 是背景主色调，我们同样可以把它做成一个shader属性。后面会给出。而在B通道上减去 0.07 * p . y 可以当成是一个轻微的效果修正，即在y方向上，可以有些许颜色变化，其中0.07也是一个经验值，可以更改。

心的绘制

心形的计算代码很简单。这里画心的原理是，判断该像素点是否在心的内部，如果在就是用心的颜色绘制，否则使用背景颜色绘制：

[cpp]view plaincopyprint? 
   
 vec3 col = mix( bcol, hcol, smoothstep( -0.01, 0.01, d-r) );  

其中我们已经讲过了bcol的计算。这里我们先忽略hcol，后面再讲，我们这里可以把它当成是一个已知的心的颜色。 smoothstep( -0.01, 0.01, d-r) 决定了我们是使用背景颜色还是心的颜色。当它值为0时，表示该像素不在心形内，则使用背景颜色，返回1时，则使用心的颜色；否则，就在背景颜色和心的颜色之间进行插值。而 smoothstep( -0.01, 0.01, d-r) 的返回值范围就是[0, 1]。 smoothstep 是CG函数，当第三个参数比-0.01小时，返回0，比0.01大时返回1，如果在-0.01和0.01之间，则返回0到1之间的值。这里， d-r 其实已经表明该像素是否在心形内（后面会讲原因）：若 d-r > 0，则在心形内，若 d-r < 0，则在心形外。那么为什么这里要使用smoothstep呢？其实是为了使心形的边缘模糊化，更美观。下面左图是模糊后的结果，而右图是没有模糊的结果：

smoothstep控制模糊效果的原理在于，在心形的边界部分，d-r的值在正负0左右波动，我们可以通过添加一个[-0.01, 0.01]范围内的平缓过渡，来平缓d-r的值在正负交界处的突变。当然，我们可以更改0.01的值，来控制模糊范围。例如，如果我们改成0.05，那么效果如下：

重要：mix+smoothstep的组合，是实现这种模糊效果的很常见的搭配！

心的形状

下面，我们来解释，为什么d-r表示该像素是否在心形内。相关代码如下：

[cpp]view plaincopyprint? 
   
 // shape  
 float a = atan(p.x,p.y)/3.141593;  
 float r = length(p);  
 float h = abs(a);  
 float d = (13.0*h - 22.0*h*h + 10.0*h*h*h)/(6.0-5.0*h);  

我们先来看a的含义。它是该像素对应方向的反正切值和π相除的结果。 atan 对应CG中的 atan2 函数，它的值域为[-π, π]。我们可以理解为，它返回的是X轴旋转到该方向所需要转过的角度（不超过正负180°）。因此，a得到的其实是一个范围在[-1.0, 1.0]之间的浮点值。这里注意计算反正切时x和y方向对调了，这是因为我们的心形是竖立着的。我们用图像来理解a的含义。下图中，每条直线上的像素点得到的a都是相同的，我们用黄点表示，黄点距离远点的远近，表示了a的大小。我只画了一侧是因为另一侧的a值为负。

这样，我们就可以通过判断该像素对应方向的长度r和a的差来判断该像素是否在心形内了。如果我们以a-r为依据而非d-r，我们会得到下面的结果：

可以看出，心形只有一侧，而且看起来比最终效果要胖了许多。这就是h和d的意义。h对a取绝对值，使得a的负值区域同样可以得到半个心形。而d对h进行修正，使用的函数表达式可以根据代码看出来，至于为什么是这个函数，大家都膜拜数学的魅力好啦。。。

心的颜色

心的颜色这里有点难理解。我们把它拆成两部分：

[cpp]view plaincopyprint? 
   
 vec3 hcol = vec3(1.0,0.5*r,0.3)*s;  

一部分是 vec3(1.0,0.5*r,0.3) ，一部分是 s 。 vec3 ( 1.0 , 0.5 * r , 0.3 ) 完成的是一个简单的由中心向外渐变的颜色：

这个渐变色没有考虑心形的约束。而s的计算则相对复杂。它用于修正上面的渐变颜色，使得在心形内外的颜色有所区别。vec3 hcol = vec3(1.0,0.5,0.3)*s;的结果如下：

s的计算如下：

[cpp]view plaincopyprint? 
   
 // color  
 float s = 1.0-0.5*clamp(r/d,0.0,1.0);  
 s = 0.75 + 0.75*p.x;  
 s *= 1.0-0.25*r;  
 s = 0.5 + 0.6*s;  
 s *= 0.5+0.5*pow( 1.0-clamp(r/d, 0.0, 1.0 ), 0.1 );  

其实源码中新一行是没用的，因为第二行直接赋值了。我用图例来表示每一步的变化。我们先把所有的计算注释掉，然后依次取消注释来看看发生了什么变化。图片如下：

从图片我们可以直观的看出，第一行根据p的x方向来得到一个在x方向上的渐变，第二行在此基础上添加了根据p的距离来产生的渐变，虽然不明显但可以看出新的渐变有了弧形，第三行则是使用类似半兰伯特的方法，增亮了左侧暗部区域，而最后一行则关键的分出了心形内外的区域颜色。

重要：最后一步中，使用pow+clamp分割区域的方法也是我们值得借鉴的地方。

心的跳动

动画的部分肯定离不开数学函数图像的帮助。我们来看这里用到的计算：

[cpp]view plaincopyprint? 
   
 // animate  
 float tt = mod(iGlobalTime,1.5)/1.5;  
 float ss = pow(tt,.2)*0.5 + 0.5;  
 ss = 1.0 + ss*0.5*sin(tt*6.2831*3.0 + p.y*0.5)*exp(-tt*4.0);  
 p *= vec2(0.5,1.5) + ss*vec2(0.5,-0.5);  

第一行计算了周期时间tt，这里的周期是1.5秒，当然我们可以自己改动。

下面ss的计算就是利用函数图像来模拟动画效果。它的函数图像如图所示（这里去掉了p.y的影响部分）：

如图，这个函数是一个在y轴上、数值1附近跳动的函数。

最后一行，p *= vec2(0.5,1.5) + ss*vec2(0.5,-0.5);，我们对x和y方向使用了的参数，是因为我们想要心是在水平方向上收缩、竖直方向上拉伸的动画效果，当然我们也可以修改它。

Shader增强版

我将一些参数设为shader的属性，以便在面板中调节。这些属性有：背景颜色，心的颜色，背景的离散洗漱，心的边缘模糊洗漱，以及跳动的时间周期。

[cpp]view plaincopyprint? 
   
 Shader "shadertoy/Heart" {  
     Properties {  
         _BackgroundColor ("Background Color", Color) = (1.0, 0.8, 0.7, 1.0)  
         _HeartColor ("Heart Color", Color) = (1.0, 0.5, 0.3, 1.0)  
         _Eccentricity ("Eccentricity", Range(0, 0.5)) = 0.25  
         _Blur ("Edge Blur", Range(0, 0.3)) = 0.01  
         _Duration ("Duration", Range(0.5, 10.0)) = 1.5  
     }  
       
     CGINCLUDE  
       
     #include "UnityCG.cginc"    
     #pragma target 3.0    
       
     #define vec2 float2  
     #define vec3 float3  
     #define vec4 float4  
     #define mat2 float2x2  
     #define iGlobalTime _Time.y  
     #define mod fmod  
     #define mix lerp  
     #define atan atan2  
     #define fract frac   
     #define texture2D tex2D  
     // 屏幕的尺寸  
     #define iResolution _ScreenParams  
     // 屏幕中的坐标，以pixel为单位  
     #define gl_FragCoord ((_iParam.srcPos.xy/_iParam.srcPos.w)*_ScreenParams.xy)    
                    
     vec4 _BackgroundColor;  
     vec4 _HeartColor;  
     float _Eccentricity;  
     float _Blur;  
     float _Duration;  
       
     struct vertOut {        
         float4 pos : SV_POSITION;        
         float4 srcPos : TEXCOORD0;      
      };      
       
      vertOut vert(appdata_base v) {      
          vertOut o;      
          o.pos = mul (UNITY_MATRIX_MVP, v.vertex);  
          o.srcPos = ComputeScreenPos(o.pos);     
          return o;      
      }  
        
      vec4 main(vec2 fragCoord);  
           
      fixed4 frag(vertOut _iParam) : COLOR0 {    
         vec2 fragCoord = gl_FragCoord;  
         return main(fragCoord);  
      }    
       
      vec4 main(vec2 fragCoord) {  
         vec2 p = (2.0*fragCoord.xy-iResolution.xy)/min(iResolution.y,iResolution.x);  
       
         p.y -= 0.25;  
           
         // background color  
         vec3 bcol = vec3(1.0,0.8,0.7-0.07*p.y)*(1.0-0.25*length(p));  
         bcol = _BackgroundColor.xyz * (1.0-_Eccentricity*length(p));  
           
         // animate  
         float tt = mod(iGlobalTime,1.5)/1.5;  
         tt = mod(iGlobalTime,_Duration)/_Duration;  
         float ss = pow(tt,.2)*0.5 + 0.5;  
         ss = 1.0 + ss*0.5*sin(tt*6.2831*3.0 + p.y*0.5)*exp(-tt*4.0);  
         p *= vec2(0.5,1.5) + ss*vec2(0.5,-0.5);  
           
         // shape  
         float a = atan(p.x,p.y)/3.141593;  
         float r = length(p);  
         float h = abs(a);  
         float d = (13.0*h - 22.0*h*h + 10.0*h*h*h)/(6.0-5.0*h);  
           
         // color  
         float s = 1.0-0.5*clamp(r/d,0.0,1.0);  
         s = 0.75 + 0.75*p.x;  
         s *= 1.0-0.25*r;  
         s = 0.5 + 0.6*s;  
         s *= 0.5+0.5*pow( 1.0-clamp(r/d, 0.0, 1.0 ), 0.1 );  
         vec3 hcol = vec3(1.0,0.5*r,0.3)*s;  
         hcol = _HeartColor.xyz *s;  
           
         vec3 col = mix( bcol, hcol, smoothstep( -0.01, 0.01, d - r) );  
         col = mix( bcol, hcol, smoothstep( -_Blur, _Blur, d - r) );  
           
         return vec4(col, 1.0);  
     }  
       
     ENDCG  
       
     SubShader {  
         Pass {  
             CGPROGRAM  
               
             #pragma vertex vert  
             #pragma fragment frag  
             #pragma fragmentoption ARB_precision_hint_fastest     
               
             ENDCG  
         }  
     }   
     FallBack "Diffuse"  
 }  