数字电路中的时钟（一）时钟抖动和分类

抖动是时钟信号边沿事件的时间点集合相对于其理想值的离散时序变量。时钟信号中的抖动通常是由系统中的噪声或其他干扰导致的。具体因素包括热噪声、电源变化、负载条件、器件噪声以及相邻电路耦合的干扰等。

时钟信号抖动定义有多种主要是：

● 周期抖动 (Period Jitter）

● 相邻周期抖动 (Cycle to Cycle Period Jitter)

● 长期抖动 (Long Term Jitter)

● 相位抖动 (Phase Jitter)

● 时间间隔误差 (Time Interval Error or TIE)

2.1 周期抖动

周期抖动是时钟信号的周期时间（变化量）相对于一定数量、随机选定的理想时钟信号周期（定量）的偏差。如果我们能对一定数量的时钟周期进行测量，就可以计算出这一段时间测量窗口内的平均时钟周期以及其标准偏差与峰峰值。我们通常将标准偏差和峰峰值分别称作 RMS 值和 Pk-Pk 周期抖动。

许多已发表的文献中往往将周期抖动定义为测得的时钟周期与理想周期之间的差异，但在实际应用中，想要量化理想周期往往有困难。如果用示波器观察设定频率为 100 MHz 的振荡器的输出，测得的平均周期可能是 9.998 ns，而非理想周期的 10 ns。因此，在实际测量中可将测量时间窗口内的平均周期视为理想周期。

2.1.1 周期抖动应用

周期抖动在数字系统中的时序冗余度计算方面非常实用。

例如，在一个基于微处理器的系统中，处理器在时钟上升之前需要 1 ns的数据建立时间。如果时钟的周期抖动为 -1.5 ns，则时钟的上升沿可能发生在数据有效前，因而微处理器可能得到不正确的数据。该实例如图 1 所示。

                                   图 1：因时钟抖动造成的数据建立时间冲突

同样，如果另一个微处理器的数据保持时间要求为 2 ns，但时钟抖动为 +1.5 ns，则数据保持时间缩短至 0.5 ns。微处理器也会得到不正确的数据。这种情况如图 2 所示。

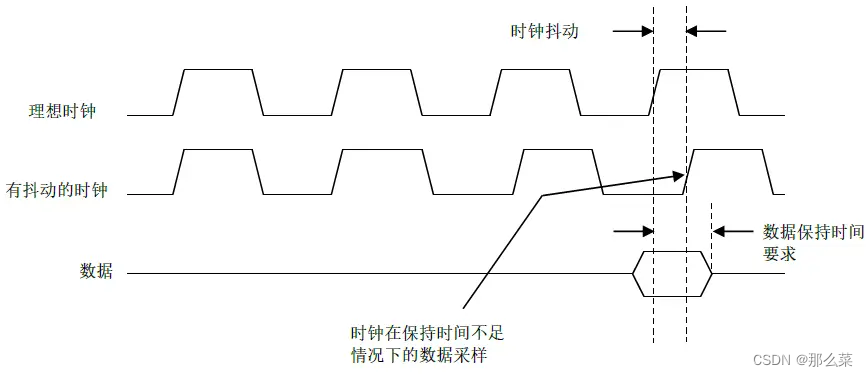
                                   图 2：因时钟抖动造成的数据保持时间冲突

2.1.2 根据 RMS 抖动计算峰峰抖动

周期抖动的任意随机性表现为高斯分布，可用均方根 (RMS)完整表达，单位是皮秒 (ps)。但是，峰峰值与计算设置和保持时间相关。下列等式是将 10,000 样本量的 RMS 抖动转换为峰峰 (Pk-Pk) 抖动：

峰峰周期抖动 = ±3.72 x（RMS 抖动） 等式 1

例如，若 RMS 抖动为 3 ps ，则峰峰抖动为 ±11.16 ps 。

等式 1 是利用高斯概率密度函数 (PDF) 表推导的结果。例如，如果样本量为 100，那么这些样本中的 99 个都将对分布均值的偏差在 ±2.327σ 以内，而且平均只有一个样本落在该区域以外。SiTime 依据 JEDEC 标准的规范，测量 10,000 样本量上的 RMS 周期抖动。

表 1：高斯概率密度函数 (PDF)

2.1.3 周期抖动测量方法

根据 JEDEC 标准 65B 的定义，周期抖动是指信号周期时间相对于一定数量、随机选定的理想时钟信号周期的偏差。JEDEC 标准进一步规定周期抖动测量的样本量应在 10,000 左右。SiTime 建议用下列流程来测量周期抖动：

1. 测量一个时钟周期的时长（上升沿至上升沿）

2. 等待随机数量的时钟周期

3. 重复上述步骤 10,000 次

4. 根据这 10,000 个样本计算平均值、标准偏差 (σ) 和峰峰值。

5. 重复上述测量 25 次。从这 25 个结果中计算平均峰峰值。

从测量 10,000 个随机样本（步骤 4）中计算出的标准偏差 (σ) 或 RMS 值非常准确。使用下列等式能够计算 RMS 值中的误差：

其中 σn 是所采集样本的 RMS（或西格玛），N 是样本大小。对于 10,000 的样本量，ErrorRMS为 0.0071σn。这种误差具有随机性，并且遵循高斯分布。最大的测量误差通常是 ±3 ErrorRMS 。

例如，如果从 10,000 个随机样本计算所得的 RMS 值为 10 ps，则 ErrorRMS 将为 0.071 ps；而且该测量所得的全部 RMS 值几乎都落在 10 ± 0.213 ps 的狭窄范围内。在实际应用中，10,000个样本集合的 RMS 误差小到足以被忽略。

虽然能从随机抽取的 10,000 样本计算出准确的 RMS 值，但峰峰值的测量难度却很大。由于周期抖动的随机性，样本的规模越大、越有可能采集到分布曲线远端上的数据点。换言之，随着收集样本的增多，峰峰值会相应体现出发散性而非收敛性。因此，我们增加了一个额外的步骤 5，以测得一致且可重复的峰峰值。

每次测量 10,000 个随机样本（步骤 4）都会产生一个标准偏差值和一个峰峰值。通过随机地重复这一过程 25 次，我们就能采集到足够的数据点，用于计算具有极高准确度的平均峰峰值。此外，我们还能通过该数据计算平均 RMS 值，但该值与每次单独运行所得到的 RMS 值极为接近。

图 3 是 Wavecrest SIA-4000C 捕捉到频率为 125 MHz 的 3.3V SiT8102 振荡器的周期抖动直方图。其代表的是从 10,000 个样本（步骤 4）所测量到的一组 RMS 和峰峰值。

图 3：10,000 个周期抖动测量的直方图

2.2  相邻周期抖动测量方法

SiTime 建议使用下列流程来测量相邻周期抖动：

1. 测量两个相邻时钟周期 T1 和 T2 的周期时间；

2. 计算 T1-T2 的值。记录这一数值的绝对值；

3. 等待随机数量的时钟周期；

4. 重复上述步骤 1,000 次；

5. 计算这 1,000 个样本的标准偏差 (σ) 和峰值。峰值是数据中的最大绝对值；

6. 重复上述测量 25 次，并从这 25 组结果中计算出平均峰值。

此外，与峰峰周期抖动类似，相邻周期抖动的峰值也会随样本数量的增多发散，而非收敛。在流程中增加步骤 6 以便从 25 个样本中取得相邻周期抖动的平均峰值。

图 4 是相邻周期抖动直方图的范例。在本例中，其峰值为 25.66 ps（两个数值的较大者：21.22ps 和 -25.66 ps 的绝对值）。

图 4：相邻周期抖动直方图

2.3 长期抖动

长期抖动测量的是在多个连续周期后时钟信号边沿与理想位置的变化。在实际测量中使用的周期数量取决于不同的应用。

长期抖动与周期抖动和相邻周期抖动不同，因为其代表的是抖动在长时间间隔期间连续时钟周期流上的抖动累积效应。因此，长期抖动有时也被称为累积抖动。长期抖动通常对图形/视频显示以及测距器等长范围遥测应用非常实用。

SiTime 建议使用下列方法测量长期抖动；在本例中，我们测量的是 10,000 个时钟上的长期抖动。

1. 测量 10,000 个连续时钟周期的时间间隔，如图 5 所示；

2. 等待随机数量的时钟周期；

3. 重复上述步骤 1,000 次；

4. 根据这 1,000 个样本计算平均值、标准偏差 (σ) 以及峰峰值。

5. 重复上述测量 25 次。从这 25 组结果中计算平均峰峰值。

图 5：测量 10,000 时钟周期时间间隔

再次重述，增加步骤 5 是因为峰峰值的发散属性。

2.4 相位抖动

一般将相位噪声描述为某一给定频率偏移处的dBc/Hz 值，也称噪声频谱密度值（例如：在 20KHz时为 -60 dBc/Hz，在 10MHz 时为 -95dBc/Hz），或是一段频率偏移范围内的连续曲线图。相位抖动是一定频率偏移范围内相位噪声的积分，以秒为单位表达。

在方波中，大部分能量均位于载波频率上。但是，部分信号能量会“泄漏到”位于载波两侧附近的频率上。相位抖动指的是相对于载波 (fc)的两个偏移频率之间包含的相位噪声能量总量。图 6是未经滤波或带宽限制的相位噪声图，阴影部分代表偏移频率 f1 和 f2 之间的相位抖动。

图 6：相位噪声图

f1 与 f2 之间的 RMS 相位抖动可用等式 3 进行定义。

其中 

 为载波频率 fc 两侧上 f1 与 f2 之间的噪声功率。

在各种数字通信应用中，计算系统的 RMS 相位抖动值之前，需要考虑传送端和接收端锁相环电路的系统组合对源于参考时钟的相位噪声的带通滤波效应。下面是常见系统应用及其相关的锁相环电路对参考时钟源相位噪声的等效带通滤波和相位抖动积分的截止频率：

● 光纤通道： 637 KHz 至 10 MHz

● 10G 以太网 XAUI： 1.875 MHz 至 20 MHz

● SATA/SAS： 900 KHz 至 7.5 MHz

如果带通滤波器传输函数是 H(f)，则滤波后的 RMS 相位抖动用等式 4 进行计算。

2.4.1 相位噪声到抖动计算器

在线相位噪声到抖动计算器， 可根据不同应用和振荡器相位噪声计算相应抖动。点击使用.

图 7：相位噪声到抖动计算器，该工具可将相位噪声转换成相位抖动(RMS)

3 时间间隔误差 (TIE)

时间间隔误差 (TIE) 是指实际信号的事件边沿时间点相对于理想信号的事件边沿时间点的时间偏差。实际上，TIE 是相位噪声频谱在时域离散信号序列的表达，以秒或 ps 为单位。图 8 是 TIE的基本概念。理想信号通常是信号处理软件利用对实际信号周期的平均估算而得到的参考信号。

                                             图 8：测量边沿的 TIE

3.1 绘制 TIE 的时间关系图

两组时钟波形的上升沿序列如图 9 顶部所示。红色脉冲是时间长度为 1000 ps 的理想时钟周期。黑色脉冲是含有抖动的时钟周期。为了简化示意图，所有时钟脉冲的下降沿在图中均没有显示。在时间序列的起点，红色时钟和黑色时钟的上升沿彼此对齐。由于抖动的存在，黑色时钟边沿，相对于红色时钟边沿，将开始在时间上偏移，有时出现在红色时钟边沿之前，有时在其之后。

图8 标识为“时钟周期”的序列表达的是随时间推移所测得的黑色时钟周期。在本例中，黑色时钟周期可能是 990 ps，也可能是 1010 ps。图8“相邻周期变化”序列展示的是黑色时钟信号每个时钟周期相较于上一个时钟周期的变化。只要两个连续时钟周期保持不变，该序列值曲线就保持平坦。但是一旦前后两个时钟周期有差异，该趋势就会改变。例如：前四个时钟周期稳定为990 ps，故“相邻周期变化”序列保持平坦；但第五个时钟的周期从 990 ps 延长到了 1010 ps ，该序列值则跳变到 +20 ps 位置，体现这一变化。换言之，“相邻周期变化“序列体现了“时钟周期”序列中相邻时钟周期的变化值。

“时间间隔误差”(TIE) 序列记录的是理想边沿（红色时钟）与实际边沿（黑色时钟）之间的累积误差。在本例中，TIE 序列值在刚开始的趋势是向负方向变化，因为前四个黑色脉冲的时钟周期每个都比理想周期短 10 ps。在累积了 -40 ps 的抖动误差后，该序列的变化趋势在第五个时钟周期改变方向，朝正方向移动，因为第五个时钟周期比理想周期长 10 ps。

TIE 测量对于使用时钟数据恢复 (CDR) 电路来从数据信号中提取参考时钟的串行数据传送系统极为有用。较大的 TIE 值表明 CDR 中的锁相环电路响应速度可能过慢，无法跟随数据流的比特率变化。

图 9：时间间隔误差 (TIE) 图

4.  实战计算

对于每一种时钟抖动进行统计和测量，可以得到其抖动的峰峰值和RMS值（有效值），峰峰值是所有样本中的抖动的最大值减去最小值，而RMS值是所有样本统计后的标准偏差。如下图1为某100M时钟的TIE、Period Jitter、Cycle to Cycle jitter的峰峰值和RMS值的计算方法。