一,幂级数的四则运算
- 设幂级数
的收敛半径为
,幂级数
的收敛半径为
,收敛域为
二,幂级数的连续性、导数和积分
- 设幂级数
,收敛区间为(-R,R)
- 则幂级数
在收敛区间(-R,R)内连续
- 则幂级数
在收敛区间(-R,R)内有各阶导数,并且可以逐项求导:
,收敛区间不变但收敛域可能改变
- 则幂级数
在收敛区间(-R,R)内可积,并且可以逐项积分:
,收敛区间不变但收敛域可能改变
三,求幂级数的和函数
- 思路:通过对幂级数的和函数求导或积分,将幂级数化为等比级数后,再用相反的运算得到原函数的和函数
- 等比级数的和函数
,首项/(1-公比),
四,例题1,求的和函数
- 求定积分
- 求导
- 得
五,例题2,求的和函数
- 求导
- 求定积分
- 得
六,例题3,求的和
- 令幂级数为
- 将
代入幂级数得:
七,例题4,如图
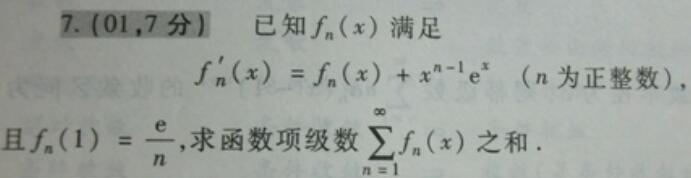
- 先解微分方程
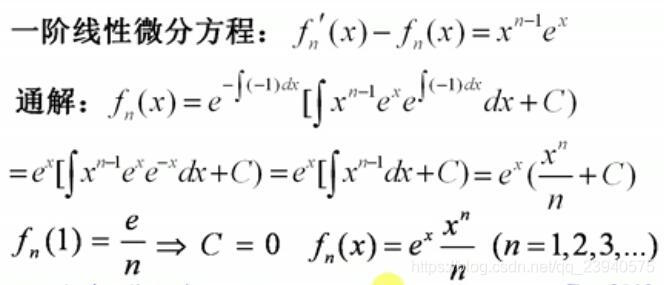
- 再求级数的和函数
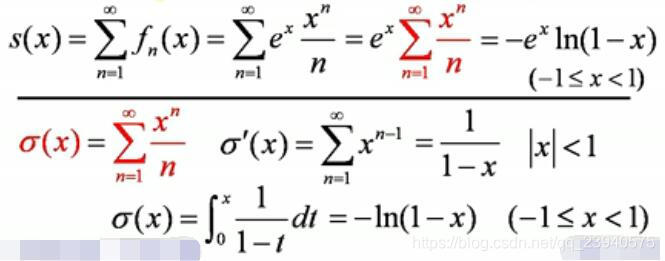
























 9058
9058

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








