MPC（1）线性时变模型预测控制

前段时间在做无人驾驶车辆模型预测控制这方面的开发，已经在Matlab/CarSim中验证过相关的算法可行性，现在对之前的工作做一个简单的记录。实际控制和理论方面还是有很大差距的，这里仅仅是参考而已。
这本书《无人驾驶模型预测控制》很有参考价值，以下几篇内容均是其中比较精华的部分摘取，有些会加上个人的一看见解，若有不当之处，劳烦指出。

线性时变模型预测控制算法是以线性时变模型做为预测模型，目前在模型预测领域应用最广的一种形式。相比非线性模型预测控制，其最大的优点就是计算较为简单，从而保证了良好的实时性。

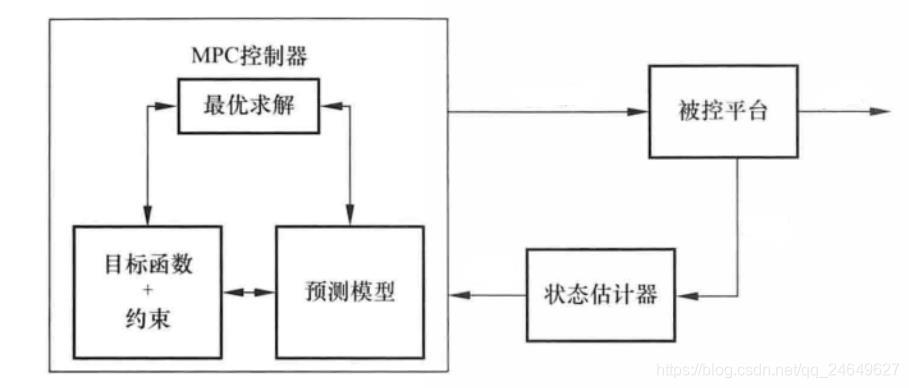
预测方程

首先，采用以下离散线性化模型：
$$x(k+1)=A_{k,t}x(k)+B(k,t)u(k)\text{\hspace{1em}(1)}$$
式中，x为状态量，u为控制量。
令
$$\xi (k|t)=\left[\begin{array}{c}x(k|t)\\ u(k-1|t)\end{array}\right]\text{\hspace{1em}(2)}$$

则可以得到一个新的状态空间表达式：
$$\xi (k+1|t)={\tilde{A}}_{k,t}\xi (k|t)+{\tilde{B}}_{k,t}\Delta u(k|t)\text{\hspace{1em}(3)}$$
$$\eta (k|t)={\tilde{C}}_{k,t}\xi (k|t)\text{\hspace{1em}(4)}$$

式中各个矩阵的定义如下，
$${\tilde{A}}_{k,t}=\left[\begin{array}{cc}{A}_{k,t}& B_{k,t}\\ 0_{m\ast n}& I_m\end{array}\right]\text{\hspace{1em}(5)}$$
$${\tilde{B}}_{k,t}=\left[\begin{array}{c}{B}_{k,t}\\ I_m\end{array}\right]\text{\hspace{1em}(6)}$$
$${\tilde{C}}_{k,t}=[C_{k,t}0]\text{\hspace{1em}(7)}$$

为了进一步简化计算，做出以下假设：
$${\tilde{A}}_{k,t}={\tilde{A}}_t,k=1,...,t+N-1\text{\hspace{1em}(8)}$$
$${\tilde{B}}_{k,t}={\tilde{B}}_t,k=1,...,t+N-1\text{\hspace{1em}(9)}$$

假设系统的预测时域Np，控制时域Nc，此时预测时域内的状态量和系统输出量可以按下下式计算：
$$\begin{gathered} \xi (t+N_p|t)={\tilde{A}}_t^{N_p}\xi (t|t)+{\tilde{A}}_t^{N_p-1}{\tilde{B}}_t\Delta u(t|t)+ \\ ...+{\tilde{A}}_t^{N_p-N_c-1}{\tilde{B}}_t\Delta u(t+N_c|t)\text{\hspace{1em}(10)} \end{gathered}$$
$$\begin{gathered} \eta (t+N_p|t)={\tilde{C}}_{t,t}{\tilde{A}}_{t,t}^{N_p}\xi (t|t)+{\tilde{C}}_t{\tilde{A}}_t^{N_p-1}{\tilde{B}}_t\Delta u(t|t)+ \\ ...+{\tilde{C}}_t{\tilde{A}}_t^{N_p-N_c-1}{\tilde{B}}_t\Delta u(t+N_c|t)\text{\hspace{1em}(11)} \end{gathered}$$

将系统未来输出时刻的输出以矩阵的形式表达：
$$Y(t)={\Psi }_t\xi (t|t)+\Theta \Delta U(t)\text{\hspace{1em}(12)}$$

式中：
$$Y(t)=\left[\begin{array}{c}\eta (t+1|t)\\ \eta (t+2|t)\\ \dots \\ \eta (t+N_c|t)\\ \dots \\ \eta (t+N_p|t)\end{array}\right]$$，
$${\Psi }_t=\left[\begin{array}{c}{\tilde{C}}_{t,t}\ast {\tilde{A}}_{t,t}\\ {\tilde{C}}_{t,t}\ast {\tilde{A}}_{t,t}^2\\ \dots \\ {\tilde{C}}_{t,t}\ast {\tilde{A}}_{t,t}^{N_c}\\ \dots \\ {\tilde{C}}_{t,t}\ast {\tilde{A}}_{t,t}^{N_p}\end{array}\right]$$，
$$\Delta U(t)=\left[\begin{array}{c}\Delta u(t|t)\\ \Delta u(t+1|t)\\ \cdots \\ \Delta u(t+N_c|t)\end{array}\right]$$,
$${\Theta }_t=\left[\begin{array}{ccccccc}{\tilde{C}}_t{\tilde{B}}_t& & 0& & 0& & 0\\ {\tilde{C}}_t{\tilde{A}}_t{\tilde{B}}_t& & {\tilde{C}}_t{\tilde{B}}_t& & 0& & 0\\ \cdots & & \cdots & & \ddots & & \cdots \\ {\tilde{C}}_t{\tilde{A}}_t^{N_c-1}{\tilde{B}}_t& & {\tilde{C}}_t{\tilde{A}}_t^{N_c-2}{\tilde{B}}_t& & \cdots & & {\tilde{C}}_t{\tilde{B}}_t\\ {\tilde{C}}_t{\tilde{A}}_t^{N_c}{\tilde{B}}_t& & {\tilde{C}}_t{\tilde{A}}_t^{N_c-1}{\tilde{B}}_t& & \cdots & & {\tilde{C}}_t{\tilde{A}}_t{\tilde{B}}_t\\ ⋮& & ⋮& & \ddots & & ⋮\\ {\tilde{C}}_t{\tilde{A}}_t^{N_p-1}{\tilde{B}}_t& & {\tilde{C}}_t{\tilde{A}}_t^{N_p-2}{\tilde{B}}_t& & \cdots & & {\tilde{C}}_t{\tilde{A}}_t^{N_p-N_c-1}{\tilde{B}}_t\end{array}\right]$$

由式（12）中可以清楚的看到，在预测时域内的状态量和输出量都可以通过当前的系统状态量和控制增量来计算出。

优化求解

在实际控制系统中，控制增量是未知的，此时只有通过设定合适的优化目标，根据此目标对预测方程进行求解出控制时域内的控制序列。不同的控制系统，可以根据控制器的情况设置不同的目标函数。一般，优化目标函数设置为如下形式：
$$\begin{gathered} J(\xi (t),u(t-1),\Delta U(t))=\sum _{i=1}^{N_p}{\Vert \begin{array}{c}\eta (t+i|t)-{\eta }_{ref}(t+i|t)\end{array}\Vert }_Q^2+ \\ \sum _{i=1}^{N_c-1}{\Vert \begin{array}{c}\Delta u(t+i|t)\end{array}\Vert }_R^2\text{\hspace{1em}(13)} \end{gathered}$$

其中第一项为预测轨迹与参考轨迹的偏差，第二项为控制量变化量的平方差，Q和R为权重矩阵。同时，也会根据实际控制系统中，控制器所能达到的控制极限做出一定的约束，
控制量约束：
$$u_{min}(t+k)\le u(t+k)\le u_{max}(t+k),k=0,1,\dots ,N_c-1\text{\hspace{1em}(14)}$$
控制增量约束：
$$\Delta u_{min}(t+k)\le \Delta u(t+k)\le \Delta u_{max}(t+k),k=0,1,\dots ,N_c-1\text{\hspace{1em}(15)}$$
输出约束：
$$y_{min}(t+k)\le y(t+k)\le y_{max}(t+k),k=0,1,\dots ,N_c-1\text{\hspace{1em}(16)}$$

结合14 - 16式，求解出带约束的优化目标，可以得到未来一段时间的控制序列。

滚动优化

通过以上步骤，解算出控制时域内的一系列控制输入增量：
$$\Delta U_t^{\ast }=[\Delta u_t^{\ast },\Delta u_{t+1}^{\ast },\dots ,\Delta u_{t+N_c-1}^{\ast }{]}^T\text{\hspace{1em}(17)}$$
取第一个控制增量做为实际控制输入增量：
$$u(t)=u(t-1)+\Delta u_t^{\ast }\text{\hspace{1em}(18)}$$
系统按照此控制量直到下一时刻t+1。t+1时刻按照此时的参考轨迹，重复以上操作，重新得到优化后的新的控制增量。如此循环直到控制过程结束。