永磁同步电机参数辨识+最小二乘原理

已于 2024-03-19 17:39:52 修改
阅读量7.5k 收藏 203
点赞数 70
分类专栏： 电机控制 算法 控制 文章标签： simulink 算法 电机控制 PMSM
于 2024-03-19 17:39:06 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_28149763/article/details/136848807
版权
本文介绍了最小二乘法的基本原理及其在电机参数辨识中的应用，包括常规、递推和RLS方法，以及结合遗忘因子的版本。详细推导了电阻、磁链、电感和转动惯量等参数的辨识方程，并通过电机参数辨识仿真实例验证了算法的有效性。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

文章目录

写在前面：本人能力、时间、技术有限，没有对一些细节进行深入研究和分析，也难免有不足和错误之处，欢迎交流和指正。本人写博客主要是学习过程的记录。

1、引言

最小二乘法（Least Square, LS）大约是1795年高斯在其著名的星体运动轨道预报研究工作中提出的。后来，最小二乘法成为了估计理论的基石。最小二乘法由于原理简明、收敛较快、易于编程实现等特点，在系统参数估计中应用相当广泛。
在自适应控制系统中，被控对象通常都可以不断提供新的输入输出数据，而且还希望利用这些新的信息来改善估计精度，因此常常要求对象参数能够在线实时估计。解决这个问题的方法就是采用最小二乘算法的递推算法，其基本思想可以概括为：
在这里插入图片描述

2、最小二乘法原理

在这里插入图片描述
在这里插入图片描述
下面考虑线性参数的最小二乘法处理：
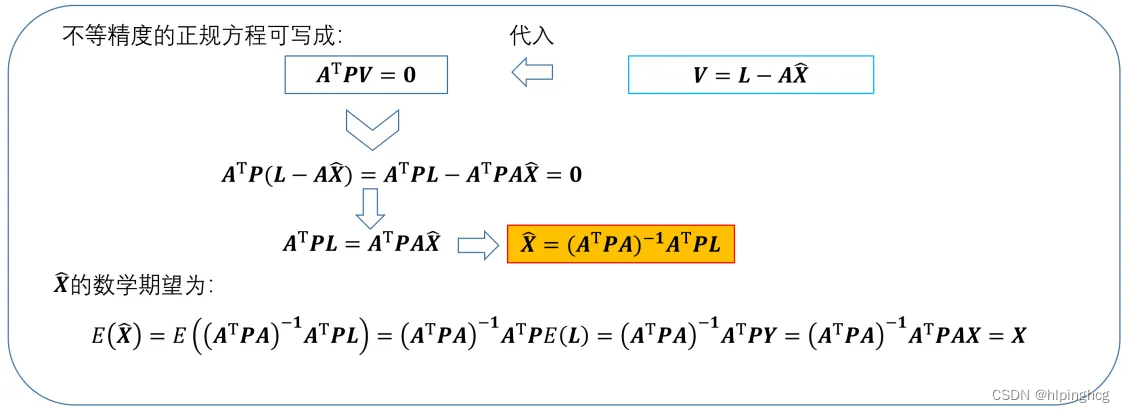
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3、最小二乘法估计与参数辨识

3.1 常规最小二乘法

在这里插入图片描述在这里插入图片描述

3.2 递推最小二乘法

在这里插入图片描述

在这里插入图片描述

3.3 递推最小二乘法RLS结合遗忘因子

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3.4 总结

在这里插入图片描述

4、电阻和磁链参数辨识方程详细推导

4.1 表贴式电机

注：我的原文做了很多公式推导，这里只给精炼部分的公式，所以公式序号有点乱，之间从式（21）开始。
在这里插入图片描述
在这里插入图片描述

4.2 内嵌式电机

在这里插入图片描述
在这里插入图片描述

5、电感参数辨识方程详细推导

在这里插入图片描述
在这里插入图片描述

6、转动惯量、阻尼系数及负载转矩辨识

在这里插入图片描述

7、参数辨识仿真

7.1 模型总览

模型下载地址：永磁同步电机递推最小二乘法电机参数辨识Simulink仿真模型
在这里插入图片描述

7.2 电机及系统参数

Rs=0.6;
Ld=1.4e-3;
Lq=1.4e-3;
flux=0.034182;
J=1.1e-5;
B=1e-3;
pole=1;
fx=0.02;
speed_kp=0.028885;
speed_ki=3.8891;
speed_Ba=0.00093819;

7.3 参数辨识模块

在这里插入图片描述
这里有一点需要说明的是，按照原理没有得到很准备的转动惯量，将理论值输入和负载值加入是可以得出理论值的，这里没想通什么原因，后面解决了在更新。

  • 电阻和磁链辨识
function [F,R] = RLS_R_Phi(uq,we,iq)

%定义永久变量
persistent P_K_1 X_K_1
%判断永久变量是否已访问过,第一次进行参数初始化
if isempty(P_K_1),            P_K_1=1e4*eye(2);  end
if isempty(X_K_1),            X_K_1=[0 0]';  end

%遗忘因子lambda 0.9-1 
%lambda小，说明求解时会很快先前的数据，更注重当前的数据，但求解的值波动会更大
%lambda大，说明求解时会依然会考虑一部分先前的数据，求解的波动更小，更平滑
lambda=1;

%定义输入矩阵
phi=[we iq]';

%定义观测矩阵
y=uq;

%计算增益
K=P_K_1*phi/(lambda*eye(1)+phi'*P_K_1*phi);

%计算协方差
P_K=(eye(2)-K*phi')*P_K_1/lambda;

%更新数据
X_K=X_K_1+K*(y-phi'*X_K_1);

%保存当前时刻数据，下次备用
P_K_1=P_K;
X_K_1=X_K;

%提取结果
F=X_K(1);
R=X_K(2);

end
  • 电感辨识
function L = RLS_L(ud,we,iq)

%定义永久变量
persistent P_K_1 X_K_1 P_K X_K
%判断永久变量是否已访问过,第一次进行参数初始化
if isempty(P_K_1),            P_K_1=1e6*eye(1);  end
if isempty(X_K_1),            X_K_1=[0]';  end

%遗忘因子lambda 0.9-1 
%lambda小，说明求解时会很快先前的数据，更注重当前的数据，但求解的值波动会更大
%lambda大，说明求解时会依然会考虑一部分先前的数据，求解的波动更小，更平滑
lambda=1;

%定义输入矩阵
phi=[-we*iq]';

%定义观测矩阵
y=ud;

%计算增益
K=P_K_1*phi/(lambda*eye(1)+phi'*P_K_1*phi);

%计算协方差
P_K=(eye(1)-K*phi')*P_K_1/lambda;

%更新数据
X_K=X_K_1+K*(y-phi'*X_K_1);

%保存当前时刻数据，下次备用
P_K_1=P_K;
X_K_1=X_K;

%提取结果
L=X_K(1);

end
  • 转动惯量及阻尼系数辨识
function [J,B] = RLS_J_B(delta_wm,wm,Tm)

%定义永久变量
persistent P_K_1 X_K_1 P_K X_K
%判断永久变量是否已访问过,第一次进行参数初始化
if isempty(P_K_1),            P_K_1=1e4*eye(2);  end
if isempty(X_K_1),            X_K_1=[0.0001 0]';  end

%遗忘因子lambda 0.9-1 
%lambda小，说明求解时会很快先前的数据，更注重当前的数据，但求解的值波动会更大
%lambda大，说明求解时会依然会考虑一部分先前的数据，求解的波动更小，更平滑
lambda=0.9;

%定义输入矩阵
phi=[delta_wm wm]';

%定义观测矩阵
y=[Tm]';

%计算增益
K=P_K_1*phi/(lambda*eye(1)+phi'*P_K_1*phi);

%计算协方差
P_K=(eye(2)-K*phi')*P_K_1/lambda;

%更新数据
X_K=X_K_1+K*(y-phi'*X_K_1);

%保存当前时刻数据，下次备用
P_K_1=P_K;
X_K_1=X_K;

%提取结果
J=X_K(1);
B=X_K(2);

end

这里将负载转矩作为已知输入，另外为了验证脚本正确性，使用真实值磁链计算了输出转矩Te，从而得到相对稳定的转动惯量和阻尼系数，若使用观测的磁链误差相对很大，因此对系统的稳定性要求较高，在实际情况下还需要考虑死区补充的问题。

7.4 仿真结果

在这里插入图片描述
辨识结果：
在这里插入图片描述
磁链辨识波形（空载）
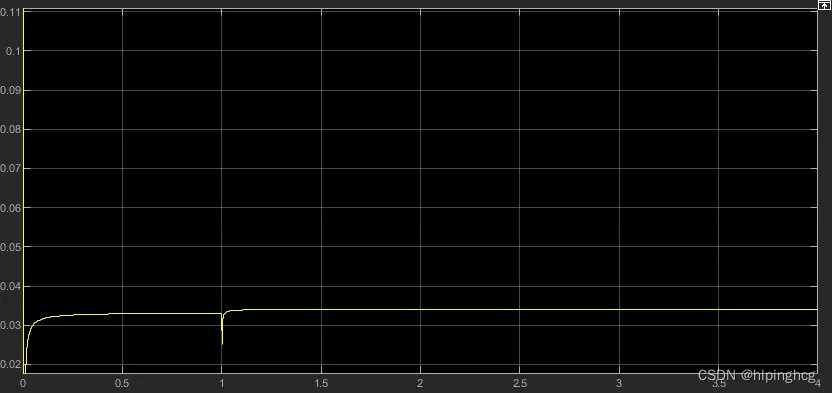在这里插入图片描述磁链辨识波形（加载）

在这里插入图片描述电阻辨识波形（空载）
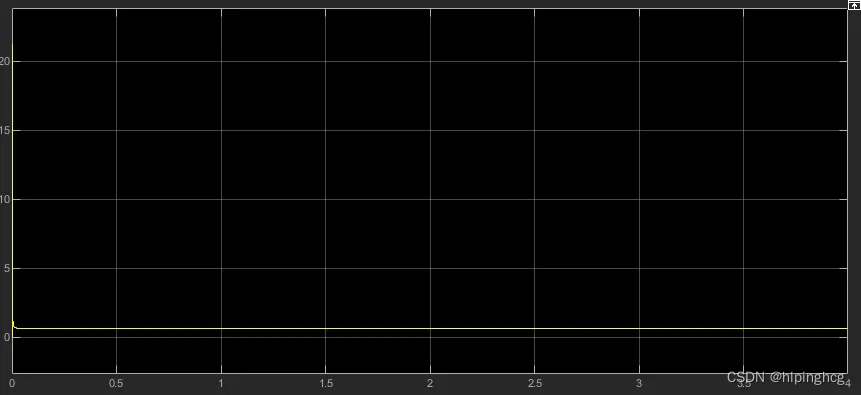
在这里插入图片描述
电阻辨识波形（加载）
在这里插入图片描述
仿真结果显示在加载的情况，参数辨识基本正确，从而一定程度上验证了算法的正确性。

参考

【1】电机仿真系列-基于最小二乘法的永磁同步电机参数辨识：
https://blog.csdn.net/c85759351/article/details/120966164?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522170964619216800213054610%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=170964619216800213054610&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2alltop_positive~default-1-120966164-null-null.142v99pc_search_result_base5&utm_term=%E6%B0%B8%E7%A3%81%E5%90%8C%E6%AD%A5%E7%94%B5%E6%9C%BA%E5%8F%82%E6%95%B0%E8%BE%A8%E8%AF%86&spm=1018.2226.3001.4187
【2】带你深入掌握最经典的最小二乘法：https://www.bilibili.com/video/BV1cv411M7wd/?spm_id_from=333.999.0.0&vd_source=8af6a0e6ffe9eaf216d5b3c382a1ee56
【3】线性回归之最小二乘法公式推导和原理介绍：https://blog.csdn.net/weixin_42364196/article/details/102964407
【4】卡尔曼滤波（1）–递归最小二乘（RLS）推导过程：
https://zhuanlan.zhihu.com/p/59532437
【5】递推最小二乘法推导（RLS）——全网最简单易懂的推导过程：
https://zhuanlan.zhihu.com/p/111758532
【6】递推最小二乘法(Recursive least square, RLS)详细推导：https://blog.csdn.net/qq_39645262/article/details/125691638
【7】递归最小二乘法与参数辨识：
https://www.bilibili.com/video/BV1Xs4y1Q74U/?spm_id_from=333.1007.top_right_bar_window_default_collection.content.click&vd_source=5f570a9f261c43941608688d2d31a4c5
【8】参数辨识最小二乘法——永磁同步电机矢量控制课题拓展：
https://blog.csdn.net/sy243772901/article/details/109342696
【9】基于递推遗忘最小二乘的永磁同步电机参数辨识：
https://blog.csdn.net/haloudama/article/details/133259025
【10】带遗忘因子的递推最小二乘法推导（C++实现）
https://blog.csdn.net/qq_34288751/article/details/130276796
【11】交流永磁同步电机的惯量辨识：
https://blog.csdn.net/jiushigedidi/article/details/127840992
【12】李文涛. 基于高频方波注入永磁同步电机无位置传感器控制技术研究[D].中国矿业大学,2021.DOI:10.27623/d.cnki.gzkyu.2020.000444.

永磁同步电机参数辨识包括初始位置检测，编码器零点位置、方向辨识
LNJZPOmIc的博客
03-17 2065
在最后，我们需要说明的是，我们的目标是提供一篇高质量的技术分析文章，而不是一个广告软文。除了初始位置检测和编码器零点位置和方向辨识外，还需要辨识电机的其他参数。电机极对数是电机的一个重要参数，它决定了电机的速度和位置控制性能。在本文中，我们将重点讨论永磁同步电机参数辨识的一些关键技术，包括初始位置检测、编码器零点位置和方向辨识、电机极对数、电阻、电感、磁链、反电势常数以及编码器零位等。我们可以利用霍尔位置传感器来检测电机的初始位置，通过读取霍尔传感器的输出信号来确定电机的初始位置。永磁同步电机参数辨识。
永磁同步电机参数迭代学习辨识
02-12
永磁同步电机参数迭代学习辨识，吕帅帅，李兵强，永磁同步电机(permanent magnet synchronous motor, PMSM)高性能伺服控制中对电机模型参数的获取精度提出严格要求，为克服传统参数辨识存在的若
PMSM永磁同步电机参数辨识仿真研究：定子电阻、DQ电感辨识与转子磁链辨识算法实践，适用于表贴式与内嵌式电机，简洁无复杂计算与滤波,PMSM永磁同步电机参数辨识仿真，适用于表贴式，内嵌式永磁同步电机:
01-20
PMSM永磁同步电机参数辨识仿真研究：定子电阻、DQ电感辨识与转子磁链辨识算法实践，适用于表贴式与内嵌式电机，简洁无复杂计算与滤波,PMSM永磁同步电机参数辨识仿真，适用于表贴式，内嵌式永磁同步电机: 辨识内容: ① 定子电阻; ② DQ电感辨识(脉冲电压法); ③ 转子磁链辨识; 上述算法，是在实践工程中提炼出的算法，无复杂的矩阵计算，无复杂的滤波算法。 带文档说明 ,核心关键词：PMSM永磁同步电机；参数辨识仿真；表贴式永磁同步电机；内嵌式永磁同步电机；定子电阻辨识；DQ电感辨识（脉冲电压法）；转子磁链辨识；实践工程算法；无复杂矩阵计算；无复杂滤波算法；带文档说明。,PMSM永磁同步电机参数简化辨识仿真：表贴与内嵌式电机实用算法详解
永磁同步电机参数辨识算法--递推最小二乘法辨识
最新发布
m0_45796409的博客
04-21 505
最小二乘法大约是1795年高斯在其著名的星体运动轨道预报研究工作中提出的。后来，最小二乘法成为了估计理论的基石。最小二乘法由于原理简明、收敛较快、易于编程实现等特点，在系统参数估计中应用相当广泛。其基本原理为：改写为递推的形式的最小二乘法估计则如下：在启动上述递推公式时需要确定初值P(0),θ(0)，一般直接令式中，a为充分大的正实数，ε为零向量或充分小的正实向量递推最小二乘法算法步骤（1）设置初始值P(0),θ(0)，输入初始数据,（2）采样当前y(k)和∮(k);
基于RLS的永磁同步电机在线参数辨识仿真模型
12-09
介绍了一种递推最小二乘法永磁同步电机参数辨识，并在MATLAB的Simulink环境下建立了基于永磁同步电机矢量控制的递推最小二乘法便是模型。
永磁同步电机_模型参考自适应_参数辨识_电阻_磁链_电感（Simulink仿真实现）
weixin_67304359的博客
12-18 947
模型参考自适应是一种用于实时控制系统的自适应控制方法。它使用一个参考模型来定义系统期望的行为，并根据实际系统的动态特性自动调整控制器的参数。这种方法适用于复杂的非线性和时变系统，并能够对不确定性和干扰进行补偿。
永磁同步电机参数辨识方法研究.pdf
07-19
讲述永磁同步电机的参数辨识方法，包括定子电阻、直轴电感和交轴电感，对初学者有很好的帮助。
【参数辨识】永磁同步电机的参数辨识
热门推荐
好梦就会趁你睡醒实现
08-15 2万+
永磁同步电机的参数辨识 辨识的参数 定子电阻Rs, 永磁磁链φf， dq轴电感Lq 第一步 建立矢量控制的电机模型 第二步 确定辨识方法--这里我才用RLS方法(递推最小二乘法) 它的主要公式由以下三部分组成 第三步 将定子电压方程转化为辨识方程 因为采用的id=0，故只需对q轴的定子电压进行辨识分析 其中协方差矩阵初值P(0)选为特征值为1e4的3*3单位矩阵，遗忘因子选为0.999，a,b,c的初值分别选为0,0，1e4。 注： w是转子旋转电角速度 它等于转子速度wm(rad/s)乘
永磁同步电机最小二乘参数辨识
05-10
永磁同步电机最小二乘参数辨识，可以运行，效果还可以
永磁同步电机控制笔记：电机参数离线辨识方法
搞电机的博客
06-20 1万+
文章目录概述1、定子电阻离线辨识1.1、定子电阻离线辨识原理1.2、定子电阻离线辨识的误差来源及补偿方法1.3、电阻离线辨识的具体方法方法一方法二2、定子电感离线辨识2.1、定子电感离线辨识原理2.1.1 输入阶跃电压2.1.2 输入脉冲电压2.1.3 输入高频电压2.2、电感辨识的具体方法及误差来源2.2.1、零状态响应法2.2.2、斜率法2.2.3、高频电压法3、永磁体磁链辨识3.1、永磁体磁链常数辨识原理及方法3.2、永磁体磁链常数辨识仿真验证3.3、小结 概述 永磁同步电机在使用转子磁场定向(foc
永磁同步电机离线参数辨识
qq_28149763的博客
11-18 3025
永磁同步电机 (PMSM) 的参数辨识可以通过在线和离线两种方式进行，这两种方法各有不同的特点和适用场景。● 在线参数辨识在线参数辨识是在电机运行的过程中实时进行参数估计。通过实时获取电机的运行数据（如电流、电压、速度等），结合估计算法，动态调整和识别电机的参数。优点：实时性：能够在电机运行过程中实时估计参数，适应参数随运行工况的变化（如温度变化、负载波动等）。适应性强：能在电机运行时检测并补偿由环境、负载和电机状态变化引起的参数漂移，提高系统的鲁棒性和适应性。
永磁同步电机多参数在线辨识研究
02-12
控制器设计往往需要精确的电机参数值来辅助设计，如无速度传感器控制、矢量 控制最优PI值设计、电压源逆变器非线性因素在线辨识/补偿等。但是随着温度、 负载和磁饱和程度的变化，永磁同步电机的定子电感、绕组电阻和转子永磁磁链 幅值等参数值大小都会随之而变化(偏离常温下设计值)。其中，温度对永磁电机 参数的影响(尤其是定子绕组电阻和转子永磁磁链幅值)是最明显也是最常见的。 对于定子绕组来说，温度的上升会导致绕组电阻值变大，而对于转子永磁来说， 温度的上升会导致转子永磁磁链幅值下降。当电机实际参数值相对于常温下的设 计参数值发生比较大变化时，会对所设计的控制系统性能造成很大影响，甚至会 让其无法工作。因此，现在主流的研究趋势是通过系统辨识理论，利用量测的电 机终端信号如定子绕组电流、电压和转速来估算定子绕组电阻和转子永磁磁链幅 值的大小，进而在线调整控制器参数和间接估算定子绕组和转子永磁的温度。本 文对该类技术进行了深入和全面的研究，提出该技术的核心是要解决“两个问题”, 并在这“两个问题”的基础上提出“三个解决方案”，最终在一套基于矢量控制的 表面式永磁同步电机试验平台上进行了验证。
永磁同步电机RLS最小二乘法参数辨识
05-17
最小二乘法（Least Square, LS）大约是1795年高斯在其著名的星体运动轨道预报研究工作中提出的。后来，最小二乘法成为了估计理论的基石。最小二乘法由于原理简明、收敛较快、易于编程实现等特点，在系统参数估计中应用相当广泛。 在自适应控制系统中，被控对象通常都可以不断提供新的输入输出数据，而且还希望利用这些新的信息来改善估计精度，因此常常要求对象参数能够在线实时估计。解决这个问题的方法就是采用最小二乘算法的递推算法，其基本思想可以概括为： 即将下式改写为递推形式，即递推最小二乘参数估计算法。可以辨识定子电阻，磁链，DQ轴电感。
基于递推最小二乘法的永磁伺服系统参数辨识
01-18
《基于递推最小二乘法的永磁伺服系统参数辨识》一文主要探讨了如何利用递推最小二乘法来提高永磁同步电机（PMSM）控制系统在复杂环境下的动态性能。文章中提到，伺服系统必须具备参数辨识和自整定能力，其中转动惯量...
基于Matlab的永磁同步电机参数辨识研究.pdf
06-26
永磁同步电机（PMSM）参数辨识技术是电机控制领域的重要研究课题，涉及到电机模型的建立、控制策略的实现以及电机性能的优化。本文档《基于Matlab的永磁同步电机参数辨识研究.pdf》深入探讨了基于Matlab平台进行PMSM...
基于递推遗忘最小二乘的永磁同步电机参数辨识
吾言@吾声
09-25 2641
目前，常见的电机电气参数辨识算法有频率响应法、模型参考自适应算法、卡尔曼滤波算法、遗传算法以及最小二乘法等，每一种辨识算法各有优缺点。其中，递推最小二乘法算法简单，易于实现，辨识过程中不需要存储所有数据，一组输入输出数据值即可进行一次计算，计算量小，实时性高。故在此以表贴式永磁同步电机为研究对象，基于递推最小二乘法实现了对永磁同步电机定子电阻和电感参数的辨识。本文主要介绍了PMSM和IPMSM参数离线辨识原理，详细推导了利用RLS辨识 PMSM定子电阻与电感及磁链的递推方程。
永磁同步电机（PMSM）参数辨识（一）
泛泛之北
10-10 1万+
1.永磁同步电机的应用场景 工业伺服驱动、新能源汽车、新能源发电、机器人、医疗设备等 2.PMSM数学模型 其中ud、uq、id和iq分别表示定子d、q轴电压和电流;Ld、Lq为定子d、q轴电感;Ｒs、ψf、ωe和ωr分别表示定子电枢电阻、转子永磁体磁链、转子电气角速度和转子机械角速度;J、D表示转动惯量和摩擦系数;Te、TL为电磁转矩和负载转矩。 对于PMSM驱动系统，为避免机械参数变化对PMSM电磁参数辨识结果的影响，考虑到其电气时间常数远小于机械时间常数，对于控制周期为微秒级的数字控制系统来说，可
永磁同步电机在线参数辨识综述
qq_44846756的博客
06-23 2540
永磁同步电机参数测定。电机的参数在运行过程中可能会发生变化，如温度变化、磁场衰减等，通过在线参数辨识可以实时地对这些变化进行补偿和校正，提高系统的鲁棒性和性能。
永磁同步电机参数辨识csdn
06-06
永磁同步电机是当今高效率、高性能电机之一。在永磁同步电机的控制中，精准的参数辨识十分重要，因为只有准确的参数才能实现最优控制。目前，几种常见的永磁同步电机参数辨识方法包括电流法、电极位置法和反演法等。 电流法是一种通过电机状态方程和装置电路方程进行辨识的方法，通过测量电机定子电流和中间电压可以确定电机的参数。电极位置法也是一种基于电机状态方程进行辨识的方法，通过测量电机转子位置和电机定子电流可以计算出电机的参数。 反演法则是通过电机的反演模型来估算电机参数。这种方法将电机正演模型中的电阻、电感和永磁体磁通量作为未知量直接进行求解。 无论采用哪种方法进行永磁同步电机参数辨识，都需要注意实际情况中电机参数的变化和不确定性。因此，可靠的参数辨识需要留有一定的容错能力，同时也需要考虑到样本数量的合理选择和信噪比的影响。总的来说，在实践应用过程中，永磁同步电机参数辨识的效果与数量、质量、精度以及环境等多方面因素息息相关。
评论 30
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

hlpinghcg

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值