//====================现控来进行闭环的原理=========================//
给定一个定常线性系统 (A，B，C)(见线性系统理论)，则在采用反馈增益矩阵 K（即比例环节）实现状态反馈后，闭环系统就变成为(A-BK，B，C)。
一级倒立摆的Simulink仿真 现在这个阶段，仿真就够实践的了。
//==================================================
LQR算法就是现代控制原理的应用。
真正的控制应该是建模，根据模型设置控制器，整定控制器参数，深感自己在这方面的功底还有很大提升空间。
//====================LQR算法=================//
//====================================//
//==================自控现控框架===================//
《自控原理》主要是在《常微分方程》和《复变函数》和《最优化》框架下研究控制系统，
《现代控制理论》是在《常微分方程》和《矩阵论》和《最优化》框架下研究控制系统。
《常微分方程》里主要涉及稳定性问题
《复变函数》和《矩阵论》主要涉及控制系统的描述问题，《复变函数》好说，《矩阵论》反传统思维，要将数学形式和实际控制问题的描述结合在一起有些难，单纯《矩阵论》一般不会指明实际问题的描述。
《最优化》主要涉及控制方法的问题，这里的最优化不是一本书，是一类问题，一个大方向，题主所说的书里，主要涉及《凸优化》这本书。
《常微分方程》、《复变函数》、《矩阵论》、《凸优化》先看，后面《自控原理》、《现代控制原理》基本是拉出来结合，一看就明白了。
就本硕的经验而言，一般控制问题，就是《复变函数》或《矩阵论》描述系统，然后找个依据《常微分方程》和《最优化》设计出来的控制方法就解决了，剩下的，多半系统不好直接描述或直接控制达不到要求，需要依据《概率与统计》的方法重新探讨，基本不在这两本书范围之内了。
作者：初学
链接：https://www.zhihu.com/question/55108426/answer/620509958
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
//=============================================//
//================自动控制原理Bode图==============================//
Bode图描述的是被控对象的特性，用开环特性看闭环特性。（开环：信号经过被控对象；闭环：信号经过被控对象后来一个单位反馈。注意只用单位反馈。）
低频段：反应稳态性能。因为给定输入信号稳定后，不再变化，频率很低，属于低频信号。
高频段：反应系统的抗干扰性能。因为噪声一般都是高频信号。
相角裕度：看bode图幅频响应 0dB处，对应的相频响应的相角裕度。
因为幅频响应0dB处，被控对象对输入信号的幅值增益为1，相当于加入单位反馈后的闭环系统的前向通道增益为1。
当bode图相频响应为-180°时，就变成了单位正反馈。所以0dB处相频响应的应该离-180°越远越好。
（正弦信号相角改变180°，就相当于添负号，再通过负反馈就变成了正反馈）
bode图
串联校正：增加一个串联环节，改变bode图，相当于改变被控对象的系统特性。（反馈都是用单位反馈，反馈的环节并不改变）
//====================现控========================================//
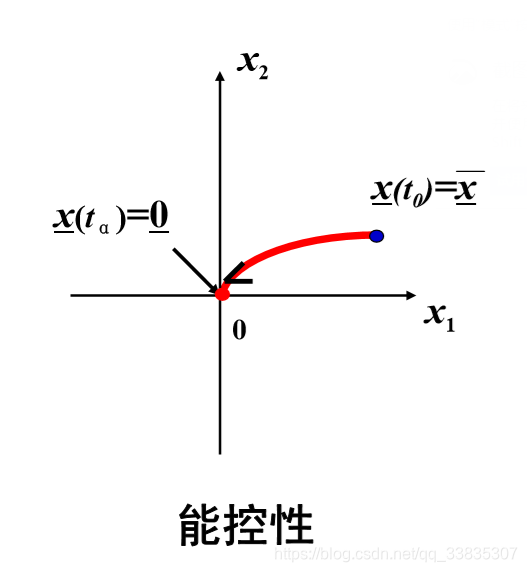
x1、x2是系统的状态变量，x(t0)是其中一个状态，x(ta)也是其中一个状态。
对于所有的状态（平面上所有的点），都能控回原点，该系统才是“完全可控的”。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
