
图片来自大名鼎鼎的Crest Ocean项目截图,其波动算法为Gerstner Waves
因为HDRP项目需要一套水,现有的水都比较简陋,所以又双叒叕在做玩具
主要是 Gerstner Waves 和 Statistical Wave Models
Gerstner Waves
1. Gerstner函数
在GPU Gems 第一部分 第一章 用物理模型进行高效水模拟 中提供了Gerstner函数:
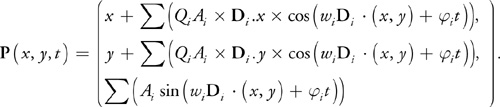
其中 Q i Q_i Qi是控制波坡度的参数。对于单个波 i i i, Q i = 0 Q_i = 0 Qi=0 会得到正常的正弦波,而 Q i = 1 / ( w i A i ) Q_i =1/ (w _i A_i) Qi=1/(wiAi) 可以给出尖峰的波形。我们可以提供可调参数到面板,使用 Q i = 1 / ( w i A i × N u m W a v e s ) Q_i =1/ (w _i A_i \times NumWaves) Qi=1/(wiAi×NumWaves) 控制波的平滑程度。
然后,我们可以通过分别对 x , y x,y x,y偏导,求出切线和副切线向量:
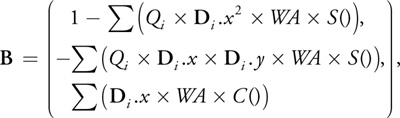
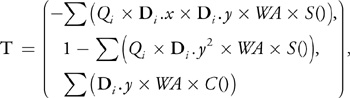
然后 B × T B \times T B×T 得到法线方向
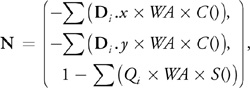
其中
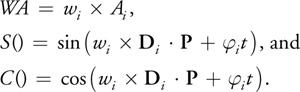
可见,计算复杂度随着波形的数量变化;文章开头是启用了8八种波形的效果,但我们往往只需要计算坐标和法线。
实现的话只需要把公式算出来罢了
float3 GerstnerWave(float2 pos, float A, float Q, float T, float Phi, float D, out float3 normal)
{
float3 outPutPos = float3(0.0f, 0.0f, 0.0f);
float2 Dir = normalize(float2(cos(D), sin(D)));
float Omega = (2.0f * 3.14159265f) / T;
float WA = Omega * A;
float Qi = Q / WA;
float TSP = _Time.y * Phi;
float fun1 = TSP + Omega * dot(Dir, pos);
float cosFun1 = Qi * A * cos(fun1);
float sinFun1 = sin(fun1);
//P(x,y,t)
outPutPos.x = Dir.x * cosFun1;
outPutPos.y = A * sinFun1;
outPutPos.z = Dir.y * cosFun1;
//法线计算
float2 P = float2(outPutPos.x, outPutPos.z);
float tempValue = Omega * dot(Dir, P) + TSP;
float cosFun2 = cos(tempValue);
float sinFun2 = sin(tempValue);
normal.xz = Dir * WA * cosFun2;
normal.y = Qi * WA * sinFun1;
return outPutPos;
}
叠加的部分,需要几次层得加几层
offsetVertex += GerstnerWave(v.vertex.xz, _A.x, _Q.x, _T.x, _Phi.x, _D.x, tempNormal);
finalNormal += tempNormal;
2. 效果
感觉很容易控制和调节,而且比较节省
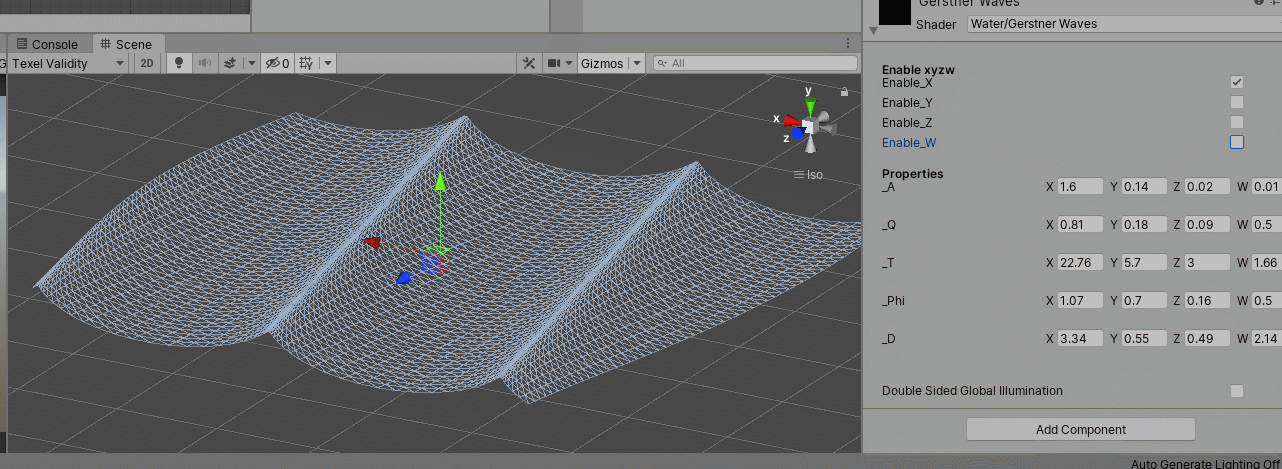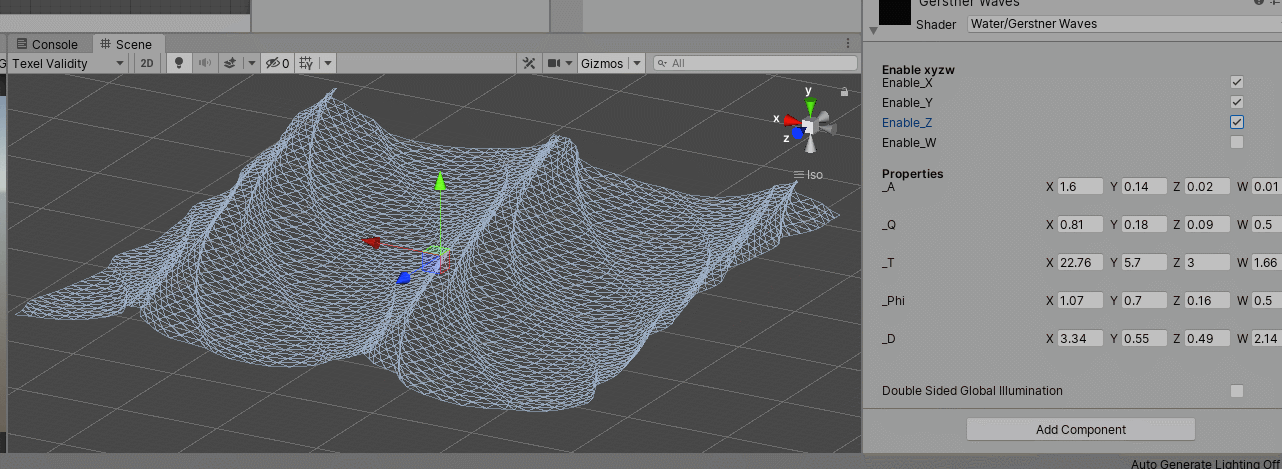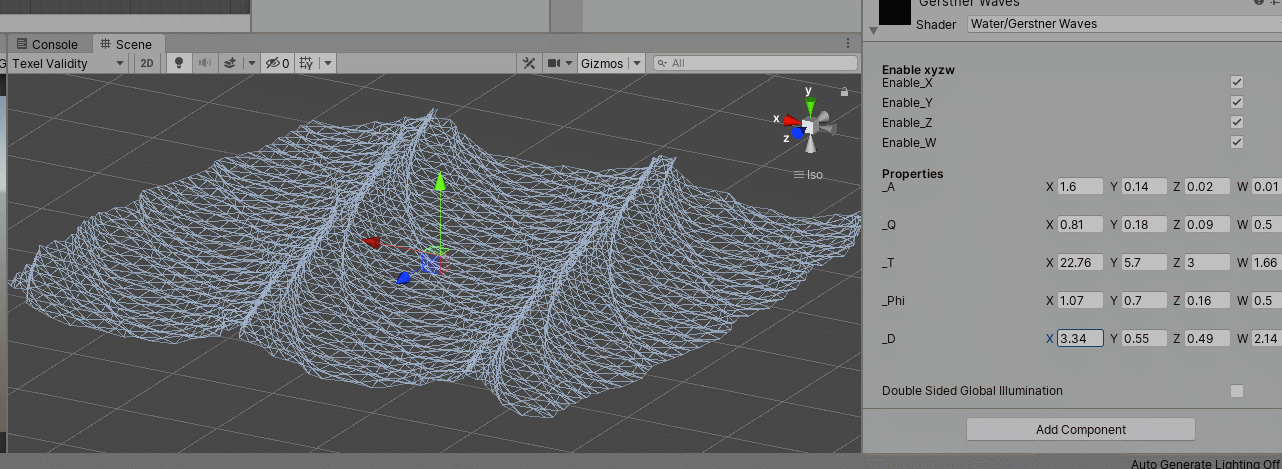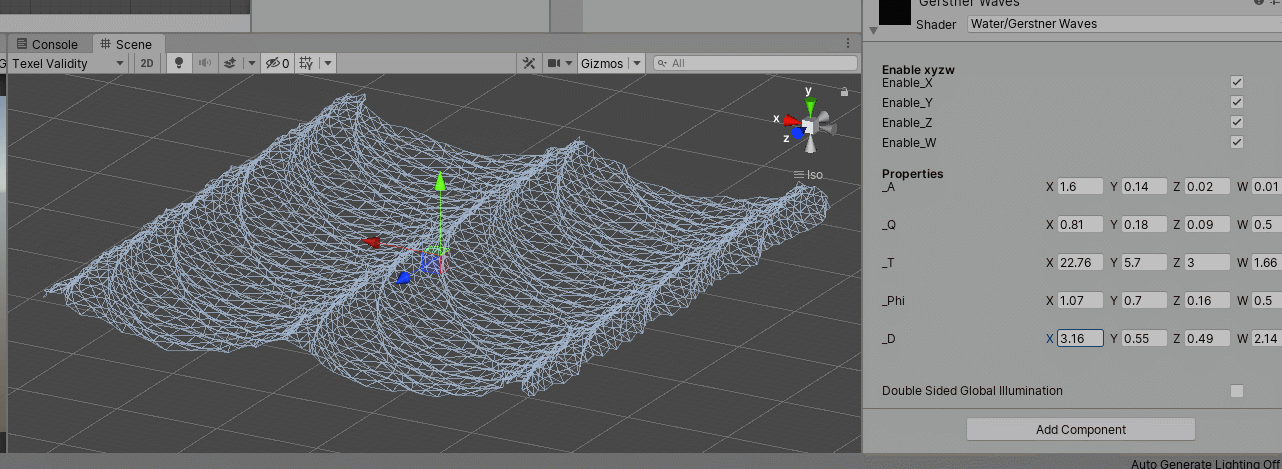
Statistical Wave Models
1. 实用的海浪算法
基于FFT的高度场表达式
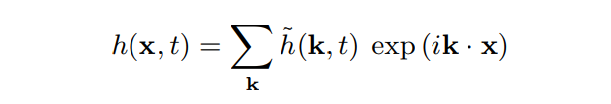
其中 t t t 是时间, k k k 是二维坐标,即水平坐标
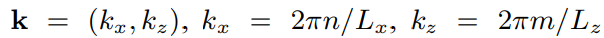
n n n 和 m m m 是整数,N、M是傅里叶变换的规模,必须是2的幂次方; L是网格的大小
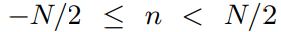
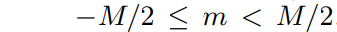
x x x 为水平离散点坐标
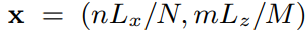
现在,我们只剩 h ( k , t ) − \stackrel{-}{h(k,t)} h(k,t)−未知了。
2. 建立随机的高度场
水波高度场的实现是由迄今为止详细阐述的原则:具有规定形式的空间谱的高斯随机数来实现的。这是直接在傅里叶域中实现的最有效的方法。波高场的傅里叶振幅可表示为
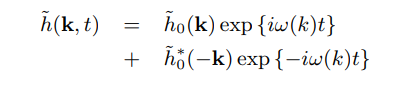
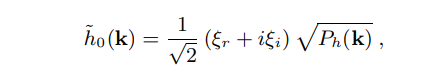
其中, ξ r \xi_r ξr 和 ξ i \xi_i ξi 是均值为0,标准差为1的高斯分布的随机数,分布形式的不同,会导致不同的效果。
原文中提到,对大量的海洋表面波浪浮标、照片和雷达测量数据的统计分析表明,波浪高度振幅几乎是统计上显著的、独立的、高斯波动,频谱统计均值可表示为:
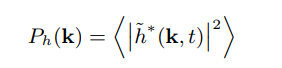
有很多经验模型模拟 P h ( k ) P_h(k) Ph(k),其中 Phillips 比较常用
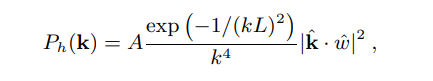
其中 L = V 2 / g L = V^2 / g L=V2/g ,V是风速,g是重力加速度, w ^ \hat w w^是风的方向。
现在,我们有了计算 h ( x , t ) h(x,t) h(x,t)所需的所有信息。
3. 优化计算
这个计算量明显要比上面的方法大太多了,为了把计算的复杂度降下来,除了尽量分离可预计算的参数之外,FFT必须得掌握
看了几篇文章,总结就是利用单位根的性质,计算基于点值表示的多项式,然后转换回去。
1. 基于点值的多项式计算
对于多项式
A ( x ) = ∑ l = 0 n − 1 a i ⋅ x i A(x) = \sum ^{n - 1}_{l = 0} a_i \cdot x^i A(x)=l=0∑n−1ai⋅xi
把不重合的差值节点 ( x 0 , x 1 , x 2 , . . . , x n ) (x_0,x_1,x_2,...,x_n) (x0,x1,x2,...,xn) 分别代入 A ( x ) A(x) A(x),得到 ( y 0 , y 1 , y 2 , . . . , y n ) (y_0,y_1,y_2,...,y_n) (y0,y1,y2,...,yn),这就是多项式的点值表示法
仅仅是表示方法并没有降低计算复杂度,复杂度的降低主要依赖于单位根的性质。
在单位圆中,单位根 w n k w^k_n wnk可表示为:
w n k = c o s ( 2 π ⋅ k n ) + i ⋅ s i n ( 2 π ⋅ k n ) w^k_n = cos(2\pi \cdot \cfrac{k}{n}) + i \cdot sin(2 \pi \cdot \cfrac{k}{n}) wnk=cos(2π⋅nk)+i⋅sin(2π⋅nk)








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 2290
2290











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








