Lattice planner
The Lattice Planner algorithm is a local motion planner,
• Sample based motion planner;
• Plan in Frenet coordinate;
• The output is a smooth, safe and collision-free local trajectory that satisfies the vehicle’s kinematics and speed constraints which is directly feed into controller.(直接反馈到控制器中)
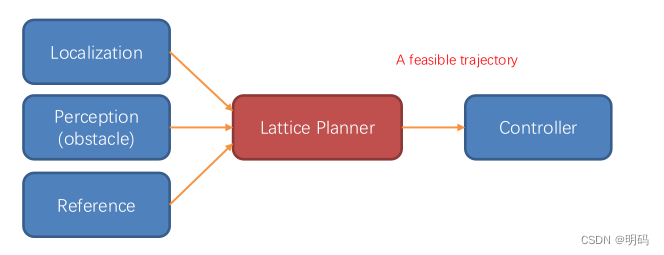
The basic process of Lattice planner:

• Frenet Coordinate
T
参考线上的可动坐标系,原点是从车辆到路径最近的r点, t 轴沿 r 处的切线tangiential方向,而 n 轴沿 r 处的pependicular方向,垂直于 t 轴。
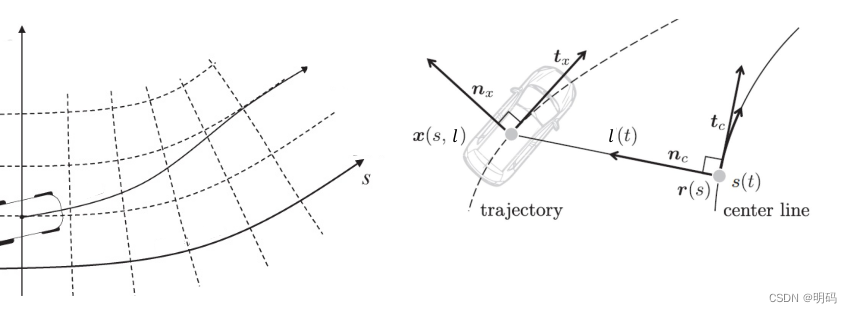
Y
为了更好地表示:相比Cartesian coordinate 将车辆的运动沿着行驶方向分解横向与纵向运动,坐标系定义在参考线上变化,更方便规划轨迹
Frenet coordinate:
[
s
,
s
˙
,
s
¨
,
l
,
l
˙
,
l
¨
,
l
′
,
l
′
′
]
\left[\mathbf{s}, \dot{\mathbf{s}}, \ddot{\mathbf{s}}, \boldsymbol{l}, \dot{\boldsymbol{l}}, \ddot{\boldsymbol{l}}, \boldsymbol{l}^{\prime}, \boldsymbol{l}^{\prime \prime}\right]
[s,s˙,s¨,l,l˙,l¨,l′,l′′]
Cartesian coordinate
[
x
→
,
v
x
,
a
x
,
θ
x
,
κ
x
]
\left[\overrightarrow{\boldsymbol{x}}, \boldsymbol{v}_{x}, \boldsymbol{a}_{x}, \boldsymbol{\theta}_{x}, \boldsymbol{\kappa}_{x}\right]
[x,vx,ax,θx,κx]
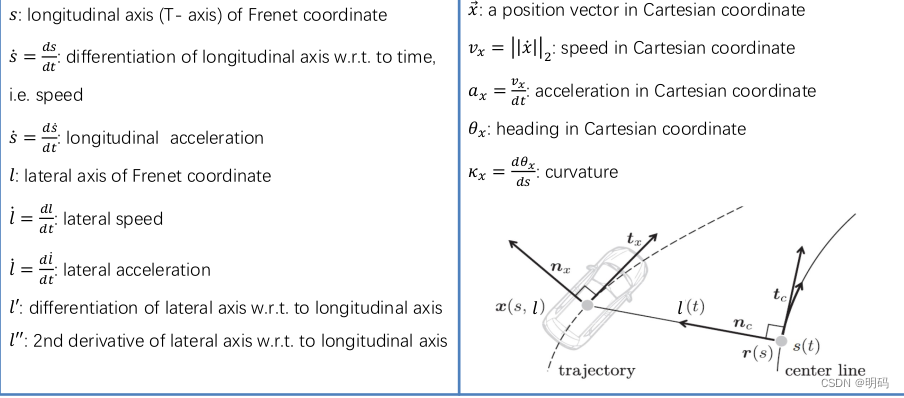
where
l
′
=
d
l
d
s
l^{'}=\frac{dl}{ds}
l′=dsdl v_x是一个标量
Frenet coordinate and Cartesian coordinate transformation
- Cartesian to Frenet

推导特别重要的公式,r(s)为原点到s(t)向量;
x ⃗ = r ⃗ + l ⋅ n c → \vec{x}=\vec{r}+l \cdot \overrightarrow{n_{c}} x=r+l⋅nc (1)
判断方向左+ 右-,即车在参考线左边为正,这个由叉乘来判断方向,n_c是在t_c逆时针方向,
n
⃗
c
=
1
l
(
x
−
x
c
,
y
−
y
r
)
t
⃗
c
=
(
cos
θ
r
,
sin
θ
r
)
n
⃗
c
×
t
c
→
=
(
y
−
y
r
)
⋅
cos
θ
r
−
(
x
−
x
r
)
sin
θ
r
\vec{n}_{c}=\frac{1}{l}\left(x-x_{c}, y-y_{r}\right)\\\vec{t}_{c}=\left(\cos \theta_{r}, \sin \theta_{r}\right)\\\vec{n}_{c} \times \overrightarrow{t_{c}}=\\\left(y-y_{r}\right) \cdot \cos \theta_{r}-\left(x-x_{r}\right) \sin \theta_{r}
nc=l1(x−xc,y−yr)tc=(cosθr,sinθr)nc×tc=(y−yr)⋅cosθr−(x−xr)sinθr
那么可以获得
l
=
sign
(
(
y
−
y
r
)
cos
θ
r
−
(
x
−
x
r
)
sin
θ
r
)
(
x
−
x
r
)
2
+
(
y
−
y
r
)
2
l=\operatorname{sign}\left(\left(y-y_{r}\right) \cos \theta_{r}-\left(x-x_{r}\right) \sin \theta_{r}\right) \sqrt{\left(x-x_{r}\right)^{2}+\left(y-y_{r}\right)^{2}}
l=sign((y−yr)cosθr−(x−xr)sinθr)(x−xr)2+(y−yr)2
在Frenet 坐标系下
l
′
l^{'}
l′
l
′
=
d
l
d
s
=
d
l
/
d
t
d
s
/
d
t
=
l
˙
s
˙
l^{\prime}=\frac{d l}{d s}=\frac{d l / d t}{d s / d t}=\frac{\dot{l}}{\dot{s}}
l′=dsdl=ds/dtdl/dt=s˙l˙
由(1)可知(向量转置)
l
=
n
c
T
(
x
−
r
)
=
(
x
−
r
)
T
n
c
l=n_{c}^{T}(x-r)=(x-r)^{T} n_{c}
l=ncT(x−r)=(x−r)Tnc
关于时间的导数
l
˙
=
(
x
˙
−
r
˙
)
T
n
c
+
(
x
−
r
)
T
n
˙
c
=
(
x
˙
−
r
˙
)
T
n
˙
c
=
(
x
˙
−
r
˙
)
T
n
c
+
(
l
n
c
)
T
n
c
˙
\dot l=(\dot{\boldsymbol{x}}-\dot{\boldsymbol{r}})^{T} \boldsymbol{n}_{\boldsymbol{c}}+(\boldsymbol{x}-\boldsymbol{r})^{T} \dot{\boldsymbol{n}}_{\boldsymbol{c}}=(\dot{\boldsymbol{x}}-\dot{\boldsymbol{r}})^{T} \dot{\boldsymbol{n}}_{\boldsymbol{c}}=(\dot{\boldsymbol{x}}-\dot{\boldsymbol{r}}) ^{T}\boldsymbol{n}_{\boldsymbol{c}}+\left(\boldsymbol{ln}_{\boldsymbol{c}}\right)^{T} \dot {\boldsymbol{n}_{\boldsymbol{c}}}
l˙=(x˙−r˙)Tnc+(x−r)Tn˙c=(x˙−r˙)Tn˙c=(x˙−r˙)Tnc+(lnc)Tnc˙ (2)
由速度定义可知:
x
˙
=
v
t
x
,
r
˙
=
s
˙
t
c
\dot{x}=v \boldsymbol{t}_{\boldsymbol{x}}, \dot{r}=\dot{s} \boldsymbol{t}_{c}
x˙=vtx,r˙=s˙tc(3)
由链式求导可知
n
c
=
d
n
c
d
t
=
d
n
c
d
s
d
s
d
t
=
s
˙
d
n
c
d
s
\boldsymbol{n}_{c}=\frac{d \boldsymbol{n}_{\boldsymbol{c}}}{d t}=\frac{d \boldsymbol{n}_{\boldsymbol{c}}}{d s} \frac{d s}{d t}=\dot{s}\frac{d \boldsymbol{n}_{c}}{d s}
nc=dtdnc=dsdncdtds=s˙dsdnc
根据Frenet坐标定义
d
n
c
d
s
=
−
κ
t
c
n
c
=
−
κ
s
˙
t
c
\frac{d \boldsymbol{n}_{c}}{d s}=-\kappa \boldsymbol{t}_{c} \\\\\boldsymbol{n}_{c}=-\kappa \dot{s} \boldsymbol{t}_{c}
dsdnc=−κtcnc=−κs˙tc (4)
将(3),(4)带入(2)中
l
˙
=
(
v
t
x
−
s
˙
t
c
)
T
n
c
−
(
ln
n
c
)
T
κ
s
˙
t
c
\dot{l}=\left(v \boldsymbol{t}_{\boldsymbol{x}}-\dot{s} \boldsymbol{t}_{\boldsymbol{c}}\right)^{T} \boldsymbol{n}_{\boldsymbol{c}}-\left(\ln \boldsymbol{n}_{\boldsymbol{c}}\right)^{T} \kappa \dot{s} \boldsymbol{t}_{\boldsymbol{c}}
l˙=(vtx−s˙tc)Tnc−(lnnc)Tκs˙tc
由于
t
c
和
n
c
t_c和n_c
tc和nc正交,那么:
l
˙
=
v
t
x
T
n
c
\dot{l}=v \boldsymbol{t}_{x}^{T} \boldsymbol{n}_{c}
l˙=vtxTnc
由于
t
x
和
n
c
t_x和n_c
tx和nc为单位向量
θ
x
,
θ
r
\theta_x ,\theta_r
θx,θr分别为t_x,t_c与x轴的夹角,可参考
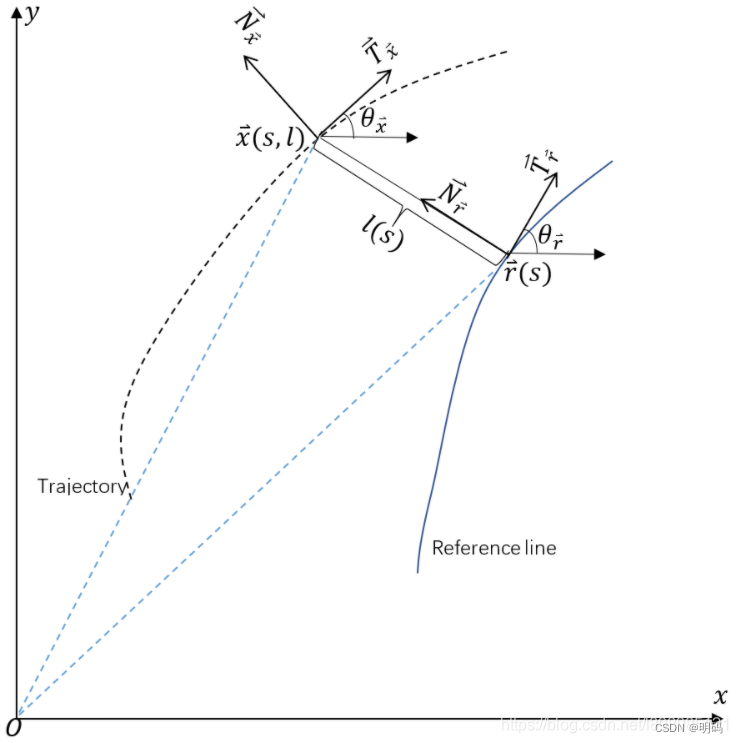
由于转置,
t
x
t_x
tx需要旋转90度,故
l
˙
=
v
sin
(
θ
x
−
θ
r
)
\dot{l}=v \sin \left(\theta_{x}-\theta_{r}\right)
l˙=vsin(θx−θr) (5)
为了得到其他量,我们又需要对(1)下手,求关于时间的导数
x
˙
=
d
(
r
+
ln
c
)
d
t
=
r
˙
+
l
˙
n
c
+
l
˙
n
c
\dot{x}=\frac{d\left(r+\ln _{c}\right)}{d t}=\dot{r}+\dot{\operatorname{l}}{ n}_{c}+\dot l n_{c}
x˙=dtd(r+lnc)=r˙+l˙nc+l˙nc
带入(3),(4)
x
˙
=
s
˙
(
1
−
κ
r
l
)
t
c
+
l
˙
n
c
\dot{x}=\dot{s}\left(1-\kappa_{r} l\right) \boldsymbol{t}_{c}+\dot{l}n _{c}
x˙=s˙(1−κrl)tc+l˙nc
由于
T
r
和
N
r
T_r和N_r
Tr和Nr正交,假定v为正,取范数
v
=
s
˙
2
(
1
−
κ
r
l
)
2
+
l
˙
2
v=\sqrt{\dot{s}^{2}\left(1-\kappa_{r} l\right)^{2}+\dot{l}^{2}}
v=s˙2(1−κrl)2+l˙2 ……(6)
由(5),(6)推导消去
s
˙
\dot s
s˙可得
(
l
˙
s
˙
)
2
=
tan
2
(
θ
x
−
θ
r
)
(
1
−
κ
r
l
)
2
=
l
′
2
\left(\frac{\dot{l}}{\dot{s}}\right)^{2}=\tan ^{2}\left(\theta_{x}-\theta_{r}\right)\left(1-\kappa_{r} l\right)^{2}=l^{\prime 2}
(s˙l˙)2=tan2(θx−θr)(1−κrl)2=l′2
通常,我们假设参考线的曲率远小于车辆最大转弯角度。还假设横向误差很小(通常车道宽度小于 4m)。因此,我们可以假设
∣
∣
1
−
κ
r
∣
∣
>
0
||1 - κ_r||> 0
∣∣1−κr∣∣>0。并且假设角度误差不会很大,
∣
θ
x
−
θ
r
∣
<
π
/
2
|\theta_{x}-\theta_{r}|<\pi/2
∣θx−θr∣<π/2
l
′
=
tan
(
θ
x
−
θ
r
)
(
1
−
κ
r
l
)
l^{\prime}=\tan \left(\theta_{x}-\theta_{r}\right)\left(1-\kappa_{r} l\right)
l′=tan(θx−θr)(1−κrl) (7)
那么可以得到s的导数
s
˙
=
v
1
−
κ
r
l
cos
(
θ
x
−
θ
r
)
\dot{s}=\frac{v}{1-\kappa_{r} l} \cos \left(\theta_{x}-\theta_{r}\right)
s˙=1−κrlvcos(θx−θr) (8)
现在开始计算
l
′
′
l^{''}
l′′
l
′
′
=
d
l
′
/
d
s
l^{\prime \prime}=d l^{\prime} / d s
l′′=dl′/ds
κ = d θ d s \kappa=\frac {d\theta} {ds} κ=dsdθ
v = d s x d t v=\frac{d s_{x}}{d t} v=dtdsx
d
θ
x
d
s
=
d
s
x
d
s
d
θ
x
d
s
x
\frac{d \theta_x}{d s}=\frac{d s_{x}}{d s} \frac{d \theta_x}{d s_{x}}
dsdθx=dsdsxdsxdθx
代入v
d
θ
x
d
s
=
d
s
x
d
s
d
θ
x
d
s
x
\frac{d \theta_x}{d s}=\frac{d s_{x}}{d s} \frac{d \theta_x}{d s_{x}}
dsdθx=dsdsxdsxdθx
代入(8)
d
θ
x
d
s
=
1
−
κ
r
l
cos
(
θ
x
−
θ
r
)
d
θ
x
d
s
\frac{d\theta_x}{d s}=\frac{1-\kappa_{r} l}{\cos \left(\theta_{x}-\theta_{r}\right)} \frac{d \theta_x}{d s}
dsdθx=cos(θx−θr)1−κrldsdθx (9)
用前面(7)式可以得
l
′
′
=
d
l
′
d
s
=
d
(
1
−
κ
r
l
)
d
s
tan
(
θ
x
−
θ
r
)
+
1
−
κ
r
l
cos
2
(
θ
x
−
θ
r
)
d
(
θ
x
−
θ
r
)
d
s
l^{\prime \prime}=\frac{d l^{\prime}}{d s}=\frac{d\left(1-\kappa_{r} l\right)}{d s} \tan \left(\theta_{x}-\theta_{r}\right)+\frac{1-\kappa_{r} l}{\cos ^{2}\left(\theta_{x}-\theta_{r}\right)} \frac{d\left(\theta_{x}-\theta_{r}\right)}{d s}
l′′=dsdl′=dsd(1−κrl)tan(θx−θr)+cos2(θx−θr)1−κrldsd(θx−θr) (10)
第一项
d
(
1
−
κ
r
l
)
d
s
=
−
(
d
κ
r
l
+
κ
r
l
′
)
\frac{d\left(1-\kappa_{r} l\right)}{d s}=-\left(d \kappa_{r} l+\kappa_{r} l^{\prime}\right)
dsd(1−κrl)=−(dκrl+κrl′)
由(9)式可知
d
(
θ
x
−
θ
r
)
d
s
=
d
θ
x
d
s
−
d
θ
r
d
s
=
1
−
κ
r
l
cos
(
θ
x
−
θ
r
)
d
θ
x
d
s
x
−
d
θ
r
d
s
\frac{d\left(\theta_{x}-\theta_{r}\right)}{d s}=\frac{d \theta_{x}}{d s}-\frac{d \theta_{r}}{d s}=\frac{1-\kappa_{r} l}{\cos \left(\theta_{x}-\theta_{r}\right)} \frac{d \theta_{x}}{d s_{x}}-\frac{d \theta_{r}}{d s}
dsd(θx−θr)=dsdθx−dsdθr=cos(θx−θr)1−κrldsxdθx−dsdθr
根据曲率的定义可知
d
θ
x
d
s
=
κ
x
,
d
θ
r
d
s
=
κ
r
\frac{d \theta_{x}}{d s}=\kappa_{x}, \frac{d \theta_{r}}{d s}=\kappa_{r}
dsdθx=κx,dsdθr=κr
l
′
′
=
−
(
d
κ
r
l
+
κ
r
l
′
)
tan
(
θ
x
−
θ
r
)
+
1
−
κ
r
l
cos
2
(
θ
x
−
θ
r
)
(
κ
x
1
−
κ
r
l
cos
(
θ
x
−
θ
r
)
−
κ
r
)
l^{\prime \prime}=-\left(d \kappa_{r} l+\kappa_{r} l^{\prime}\right) \tan \left(\theta_{x}-\theta_{r}\right)+\frac{1-\kappa_{r} l}{\cos ^{2}\left(\theta_{x}-\theta_{r}\right)}\left(\kappa_{x} \frac{1-\kappa_{r} l}{\cos \left(\theta_{x}-\theta_{r}\right)}-\kappa_{r}\right)
l′′=−(dκrl+κrl′)tan(θx−θr)+cos2(θx−θr)1−κrl(κxcos(θx−θr)1−κrl−κr) (11)
求
s
¨
\ddot {s}
s¨ 对(8)求关于时间的导数
v
˙
=
a
\dot{v}=a
v˙=a
解方程可知
a
=
s
¨
1
−
κ
r
l
cos
Δ
θ
+
s
˙
cos
Δ
θ
(
(
1
−
κ
r
l
)
tan
Δ
θ
d
Δ
θ
d
s
−
d
κ
r
l
−
κ
r
l
′
)
,
Δ
θ
=
θ
x
−
θ
r
a=\ddot{s} \frac{1-\kappa_{r} l}{\cos \Delta \theta}+\frac{\dot{s}}{\cos \Delta \theta}\left(\left(1-\kappa_{r} l\right) \tan \Delta \theta \frac{d \Delta \theta}{d s}-d \kappa_{r} l-\kappa_{r} l^{\prime}\right), \Delta \theta=\theta_{x}-\theta_{r}
a=s¨cosΔθ1−κrl+cosΔθs˙((1−κrl)tanΔθdsdΔθ−dκrl−κrl′),Δθ=θx−θr (12)
- Frenet to Cartesian
相对简单点,这也是一种优势
x
=
x
r
−
l
sin
θ
r
y
=
y
r
+
l
cos
θ
r
x=x_{r}-l \sin \theta_{r}\\y=y_{r}+l \cos \theta_{r}
x=xr−lsinθry=yr+lcosθr
由(7)可知
θ
x
=
arctan
2
(
l
′
,
1
−
κ
r
l
)
+
θ
r
\theta_{x}=\arctan 2\left(l^{\prime}, 1-\kappa_{r} l\right)+\theta_{r}
θx=arctan2(l′,1−κrl)+θr
不过 θ x \theta_{x} θx需要限制
v
=
s
˙
2
(
1
−
κ
r
l
)
2
+
l
˙
2
v=\sqrt{\dot{s}^{2}\left(1-\kappa_{r} l\right)^{2}+\dot{l}^{2}}
v=s˙2(1−κrl)2+l˙2
κ
和
a
\kappa 和 a
κ和a由(11),(12)可得
a = s ¨ 1 − κ r l cos Δ θ + s ˙ cos Δ θ ( ( 1 − κ r l ) tan Δ θ d Δ θ d s − d κ r l − κ r l ′ ) , Δ θ = θ x − θ r a=\ddot{s} \frac{1-\kappa_{r} l}{\cos \Delta \theta}+\frac{\dot{s}}{\cos \Delta \theta}\left(\left(1-\kappa_{r} l\right) \tan \Delta \theta \frac{d \Delta \theta}{d s}-d \kappa_{r} l-\kappa_{r} l^{\prime}\right), \Delta \theta=\theta_{x}-\theta_{r} a=s¨cosΔθ1−κrl+cosΔθs˙((1−κrl)tanΔθdsdΔθ−dκrl−κrl′),Δθ=θx−θr
l ′ ′ = − ( d κ r l + κ r l ′ ) tan ( θ x − θ r ) + 1 − κ r l cos 2 ( θ x − θ r ) ( κ x 1 − κ r l cos ( θ x − θ r ) − κ r ) l^{\prime \prime}=-\left(d \kappa_{r} l+\kappa_{r} l^{\prime}\right) \tan \left(\theta_{x}-\theta_{r}\right)+\frac{1-\kappa_{r} l}{\cos ^{2}\left(\theta_{x}-\theta_{r}\right)}\left(\kappa_{x} \frac{1-\kappa_{r} l}{\cos \left(\theta_{x}-\theta_{r}\right)}-\kappa_{r}\right) l′′=−(dκrl+κrl′)tan(θx−θr)+cos2(θx−θr)1−κrl(κxcos(θx−θr)1−κrl−κr)
可算推完了
sampling
Lattice planner sampling includes:
• Lateral sampling
• Longitudinal sampling
• Time sampling
采样空间
• State space: Those arising from the environment
• Control space: Those arising from vehicle mobility

• Speed planning
•Formulate lateral planning function l(s) and longitudinal planning function s(t) using polynomials based on the sampling.
•Typically, 4th or 5th order polynomials are used to ensure the smoothness of the path.

?
In cruise control (4th order example)
4次多项式拟合,不关注jerk约束,符合实际巡航需要
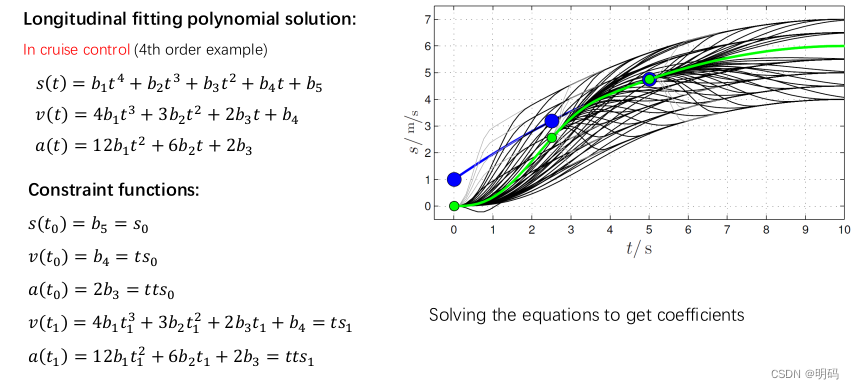
• Trajectory planning
拟合多项式

约束函数
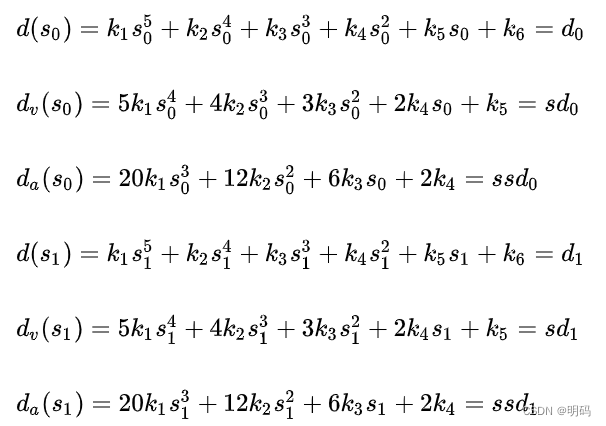
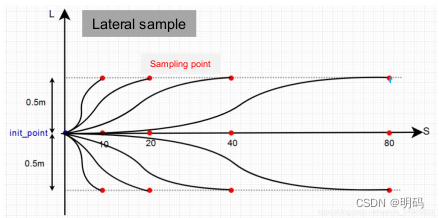
Constraint variables:
d_0 : initial lateral displacement
sd_0 : initial lateral speed
ssd_0 : initial lateral acceleration
d_1 : sampled lateral displacement
sd_1 : sampled lateral speed
ssd_1 : sampled lateral acceleration
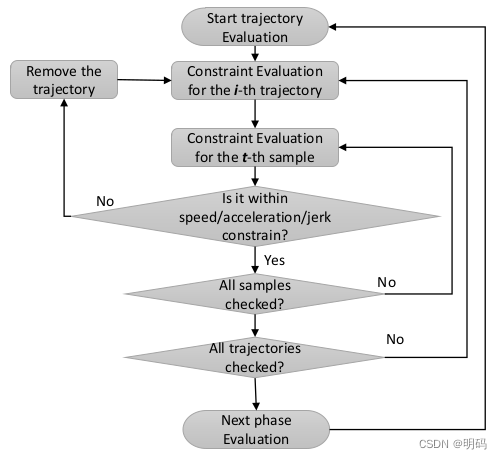
?
For every trajectory generated, it needs to be evaluated to check if it violates any constraint and remove it if it does.
代价函数
Objective: to choose a feasible path that is nearest to the static reference path, and at the same time, avoid large speed change to ensure comfortability and stay away from obstacles.

Longitudinal Objective achievement cost : to choose a feasible path that is nearest to the static reference path.
红灯停,停车线
动态改变代价

Comfort Objective: to choose a feasible path that is having less jerk
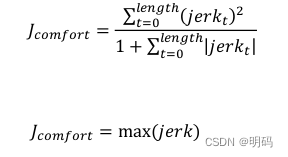
Centripetal Objective: to choose a feasible path that is having less less centripetal (向心)accel jerk .

Collision Objective: to choose a path that is furthest from obstacles

横向偏移cost,一般选择中心线,方便变道,有更多的余量
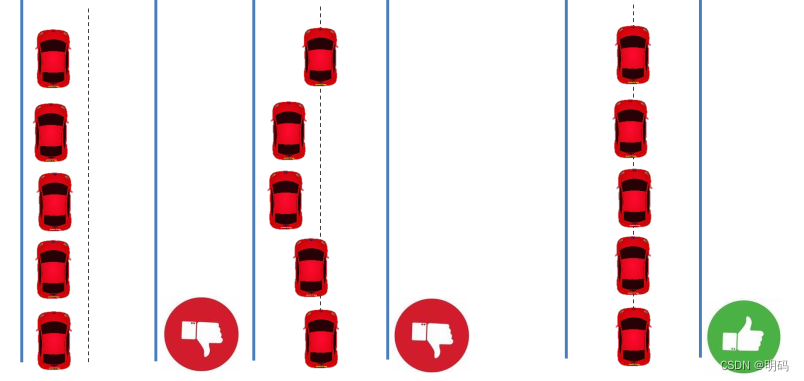 Lateral Acceleration Objective: to choose a feasible path that is having smoother lane change
Lateral Acceleration Objective: to choose a feasible path that is having smoother lane change
Reference
深蓝学院
State Space Sampling of Feasible Motions for High-Performance Mobile Robot Navigation in Complex Environments,Thomas M. Howard, Colin J. Green, and Alonzo Kelly
Frenet坐标推导过程整理
























 5807
5807











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








