基于图搜索的路径规划方法

 ps:本文的相关图片来自与深蓝学院的课件。

图搜索的基本概念

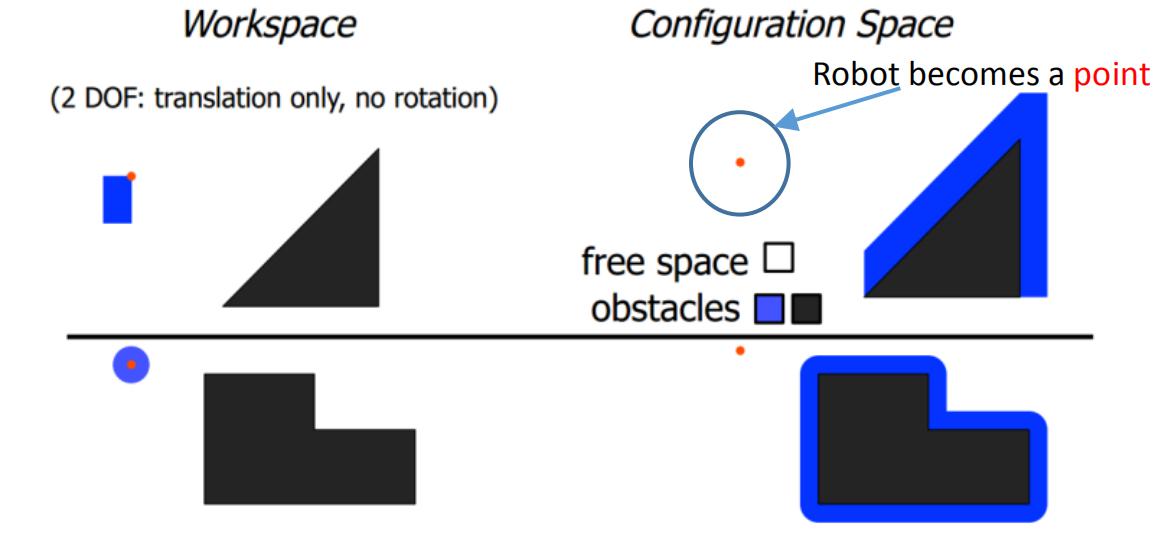
    Workspace：现实空间。

    配置空间：机器人表示为一个点，障碍物表示为无法达到的点。

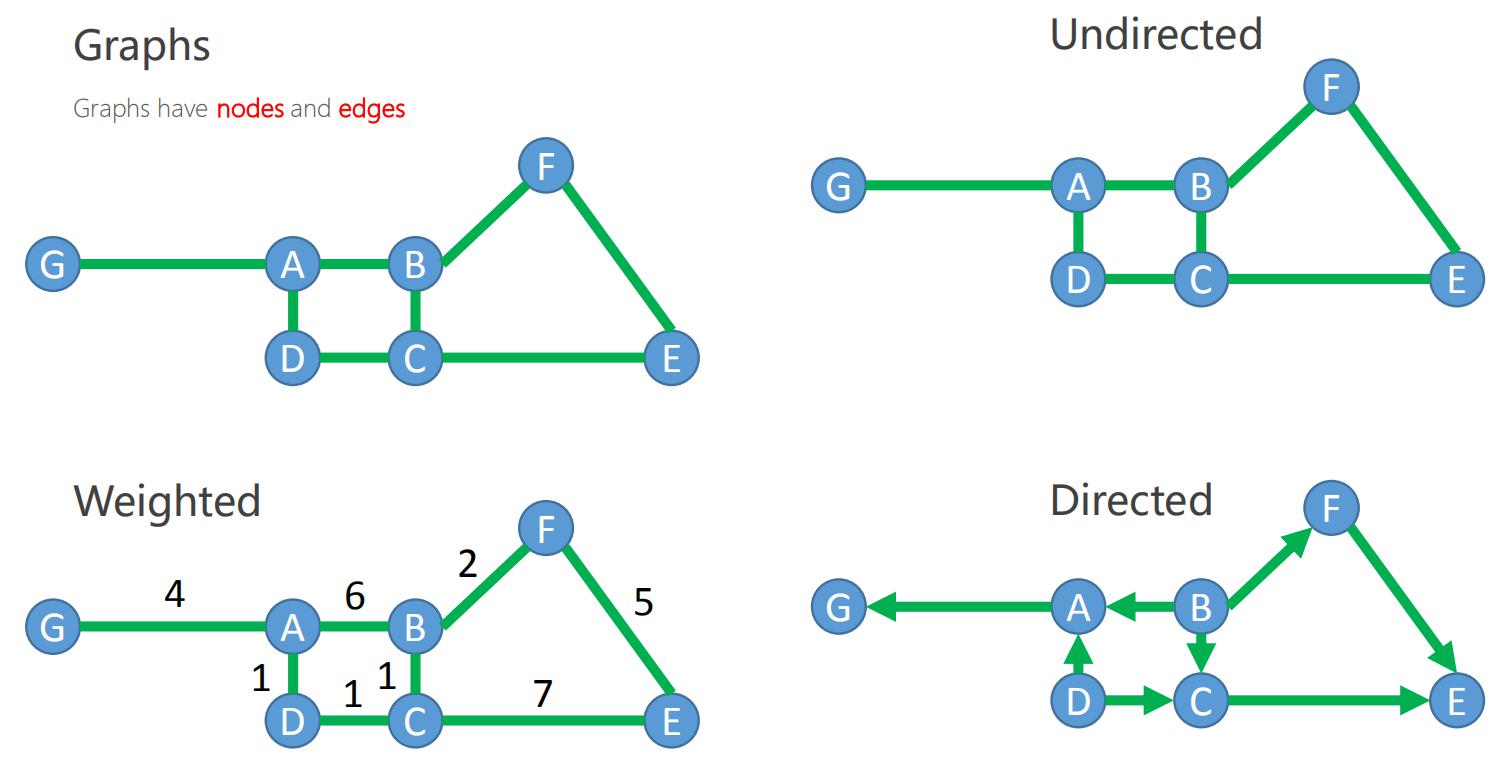
    下面是不同的图的形式：抽象图、无向图、带权重的图、有向图。

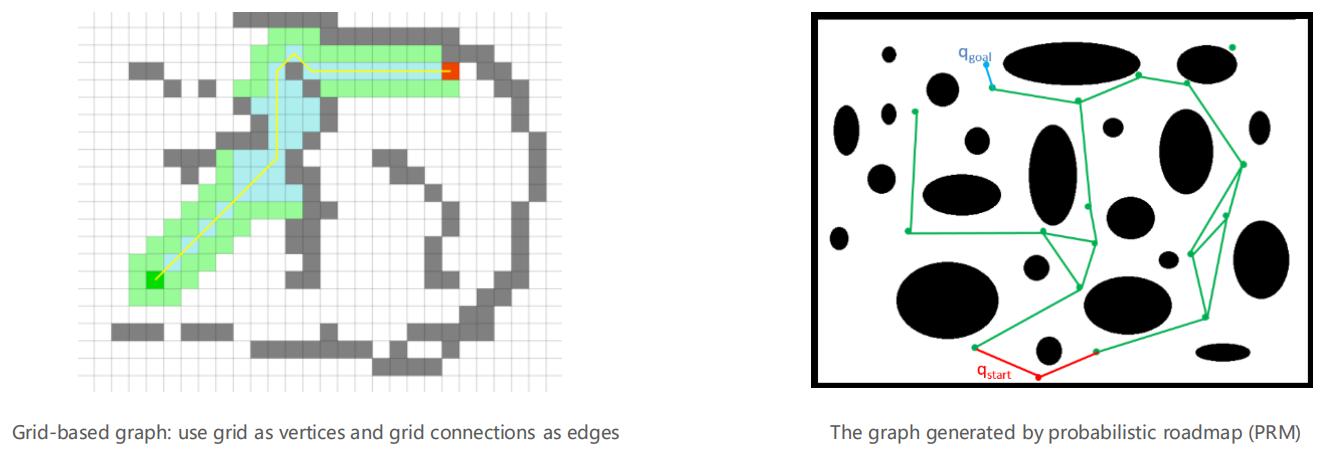
    对于一个搜索问题，都对应一个状态空间图，图中节点之间的连接性由有向或无向边表示。如下图左的栅格地图就是以每个栅格为节点而构建一个搜索图，下图右的采样地图需要人为构建一个图：

    对图进行搜索可以得到一个搜索树：

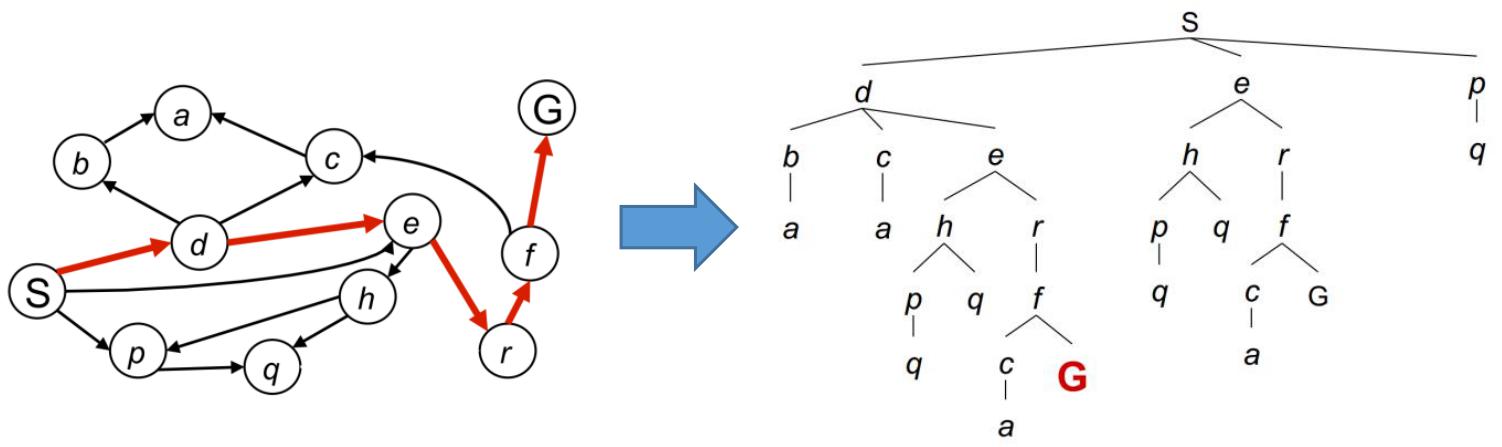
    对于多数搜索问题，一般无法构建整个树，而仅需要达到目标节点即可。

图搜索算法的框架

    

 

    循环的结束条件：当待访问节点容器为空时。为了防止循环访问，需要将访问过的节点从容器中删除，并后面不再放回。拓展节点的规则必须被设计的很好以便能够尽可能快的到达目标。

广度优先搜索(BFS)和深度优先搜索(DFS)

    BFS使用先进先出(FIFO)的容器，比如队列，进行节点的访问：

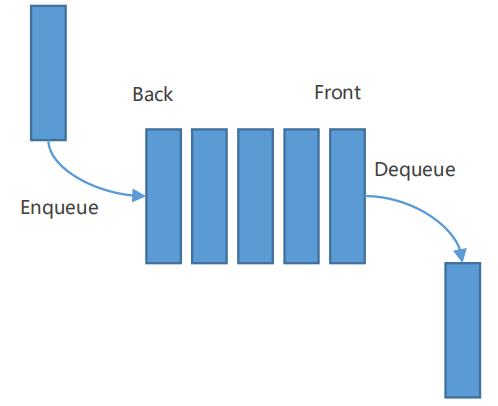
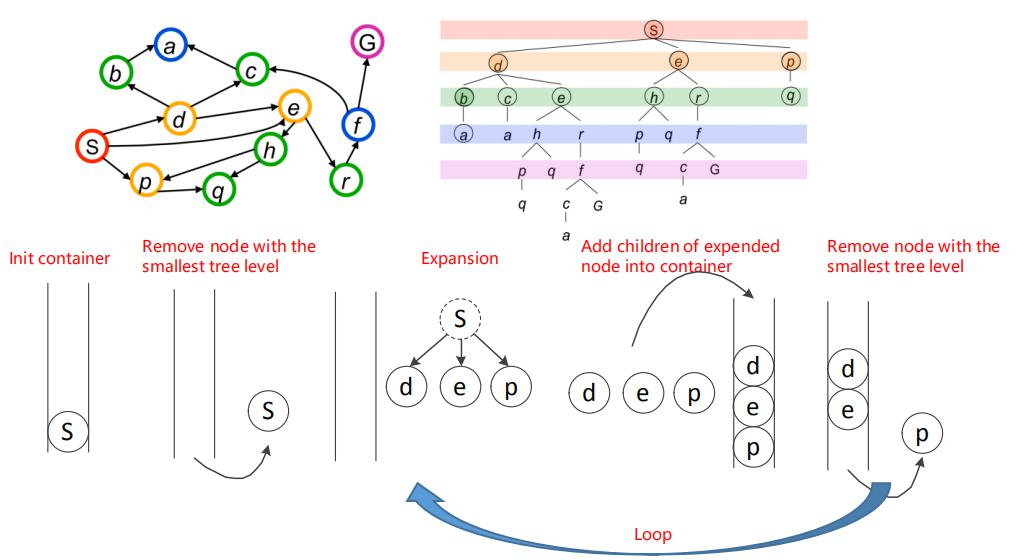
    基于FIFO容器访问节点的实例如下：

    DFS使用后进先出(LIFO)的容器，比如栈，进行节点的访问：

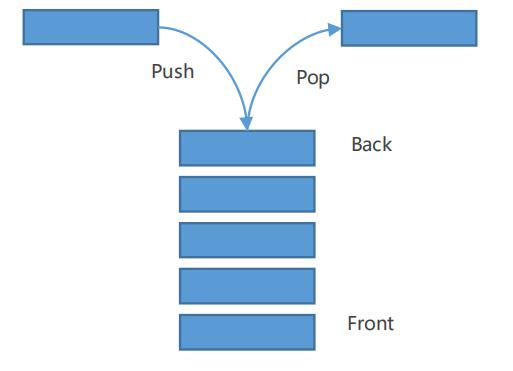
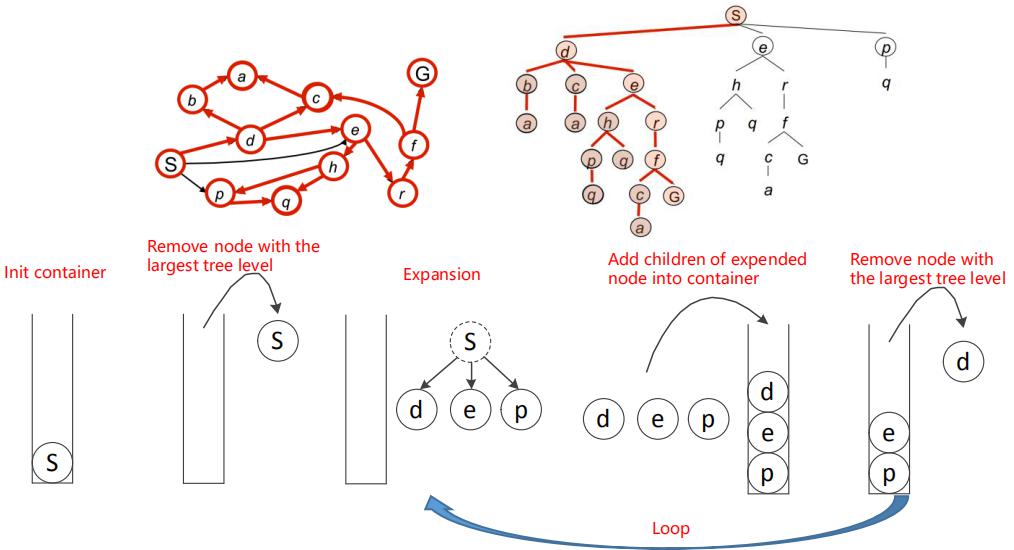
    基于LIFO容器访问节点的实例：

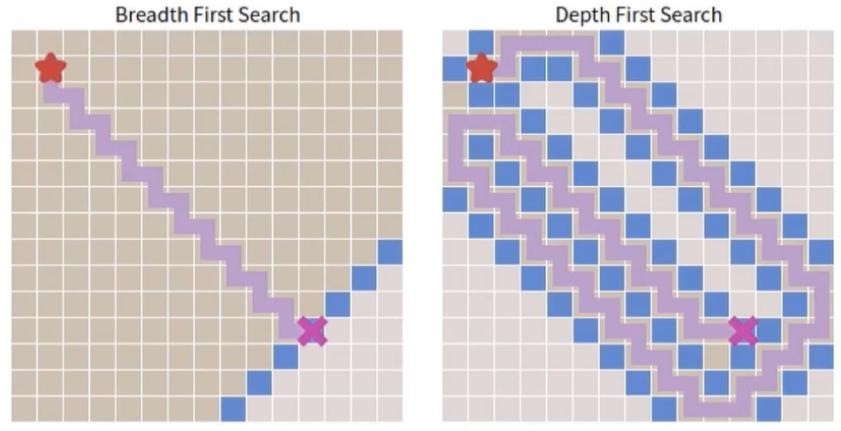
    下面是BFS和DFS两种算法进行路径规划的情况：

启发式搜索：贪心算法

    BFS和DFS在访问节点的顺序是先进或后进的，而启发式算法访问节点的顺序是根据某些规则来访问节点的，因此称为启发式算法。比如贪心算法，贪心算法根据规则（欧式距离或曼哈顿距离）来猜测节点距离目标点的远近，从而给出一个路径的方向。

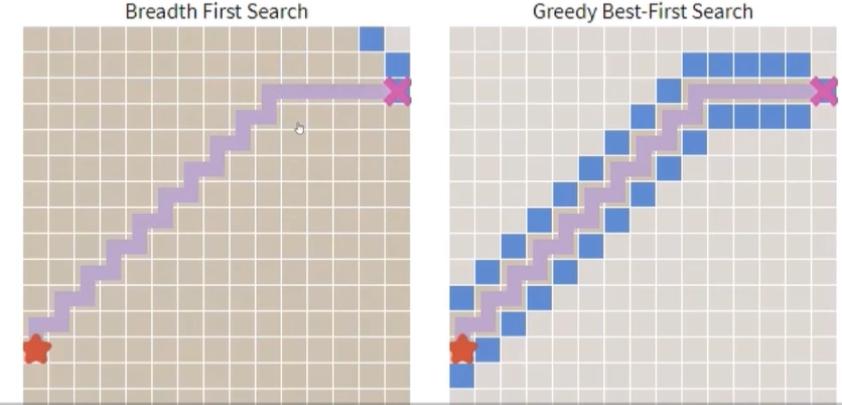
    在没有障碍物的情况下贪心算法和BFS的对比：

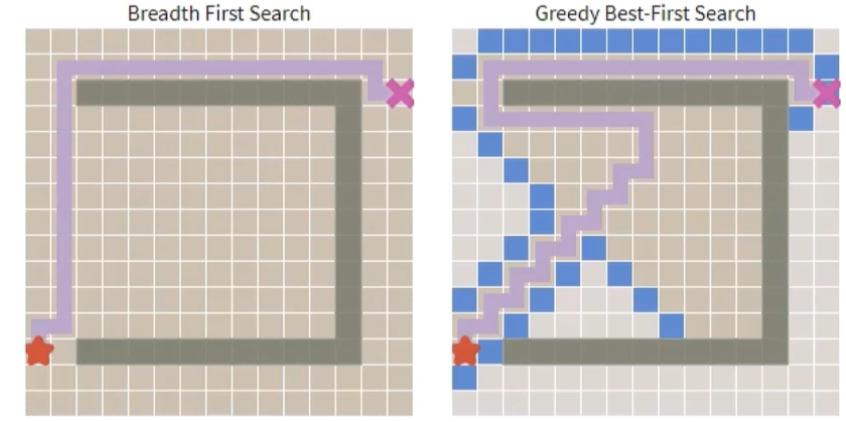
    而在另一些情况下的对比：

Dijkstra算法

    Dijkstra和贪心算法、BFS的不同之处在于访问相邻节点的顺序，Dijkstra根据最小累计代价g(n)来确定要先访问的节点。g(n)即从起点到当前点n的最小累计代价。如果相邻节点n已被访问过，但是从当前节点到该节点计算的g(n)小于它本来计算的g(n)，则更新该相邻节点的g(n)值。

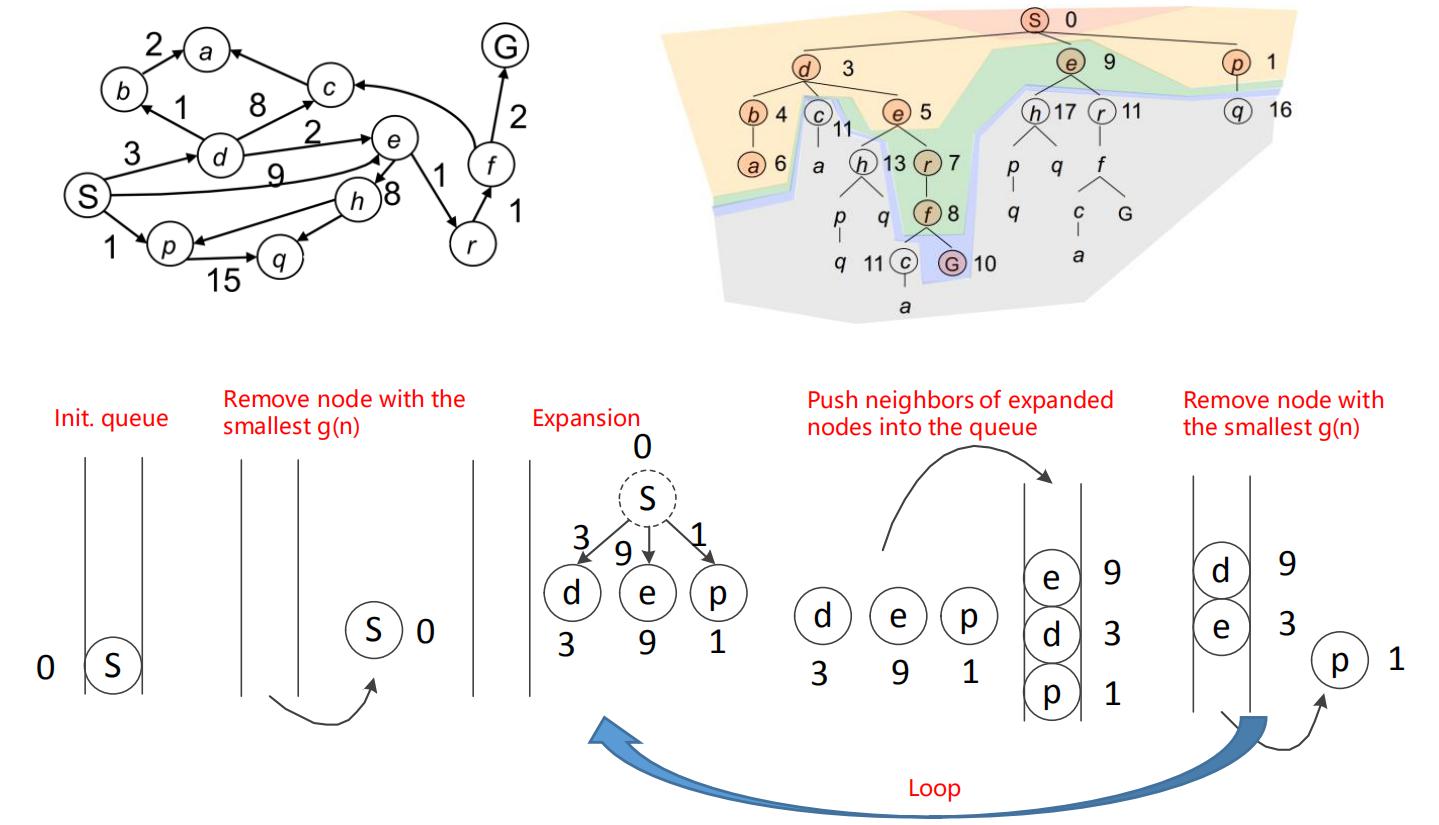
    Dijkstra的算法流程如下：

    因此Dijkstra需要使用优先级队列来作为容器，比如C++的multimap。示例如下：

    Dijkstra的优点：完备的，即如果有解肯定可以找到；找到的解肯定是最优的。

    缺点：仅可以看到累计代价，因此拓展节点的方向比较随便；没有关于全局的位置信息。 因此它搜索的节点数量会较多。

    结合Dijstra和贪心算法的优点，就得到了A*算法。

A*算法

    A*算法与Dijkstra算法整体流程基本一致，只是A*算法在拓展节点时不仅考虑累计代价g(n)，同时考虑一个从拓展节点到终点的启发式代价，比如欧式距离。因此拓展节点时对每个邻节点计算f(n)=g(n)+h(n)，选择最小f(n)的邻节点优先拓展。A*算法的算法流程如下：

    A*算法的实例如下：

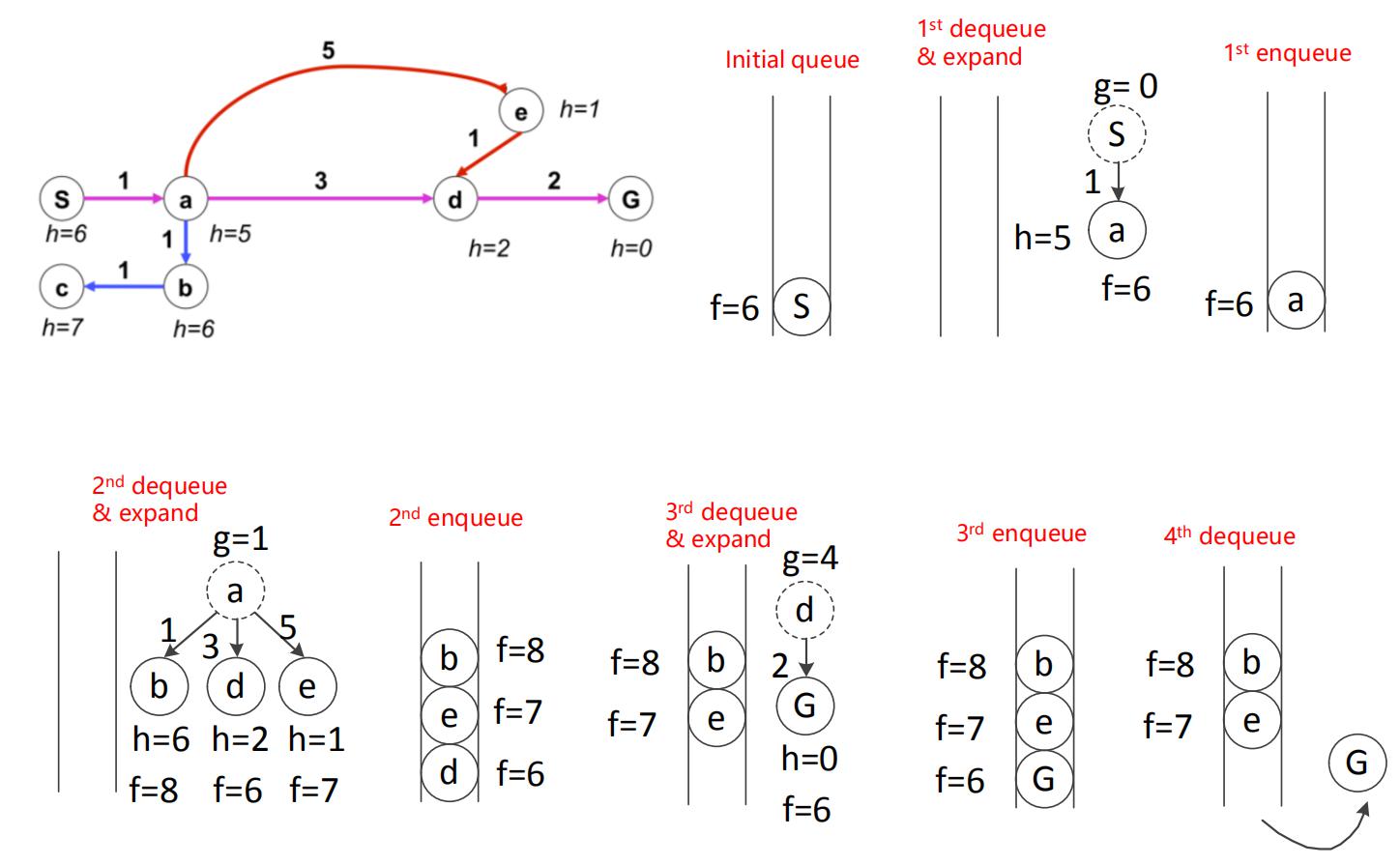
    需要注意的是，必须使得设计的启发式代价小于等于实际到目标的代价，因此设计的启发式算法必须Admissible，即h(n)<=h*(n)，h*(n)是从节点n到目标节点的真实最小代价。比如欧式距离就是Admissible的，还有h(n)=0也是。

Dijkstra和A*的对比

    Dijkstra算法在各个方向进行拓展，因此可以保证找到全局最优；而A*算法主要朝着目标的方向进行拓展，因此无法保证能找到全局最优路径，但是计算量大大减小。

Weighted A*

    对h(n)进行加权，即f(n)=g(n)+epsilon*h(n)，可以提高或减小启发式代价的权重。权重一般大于1，可以增加启发式代价的权重，可以使得A*更加贪心，因此计算量更小，但是找到最优解的可能性变小。

    在此基础上还有各种算法，包括Anytime A*，ARA*，D*等算法。

启发式函数的选择

    假设机器人可以沿着八个方向进行运动，在使用欧式距离作为启发式代价的情况下，路径的拓展节点的范围如下：

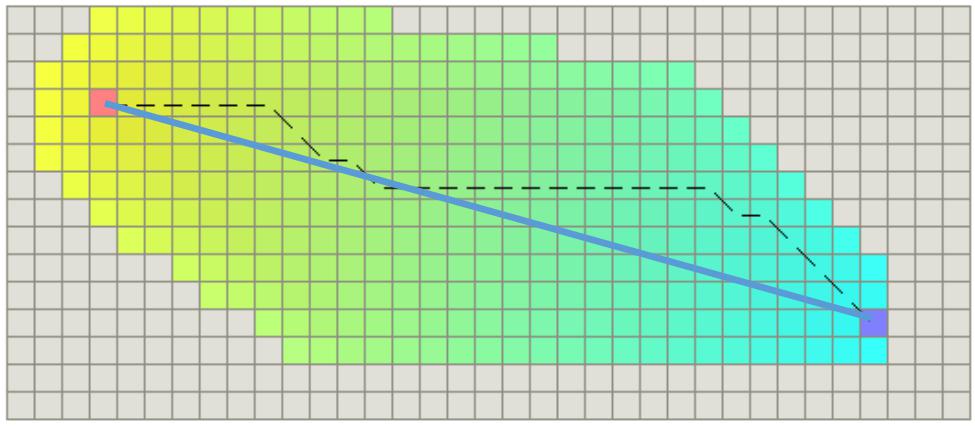
    拓展了非常多的节点，表示这个算法的低效。原因是机器人只能沿着八个方向运动，导致节点n到终点的实际代价h*(n)，比启发式代价即欧式距离大很多，即两个代价非常的不“紧贴(tight)”。因此需要找一个跟h*(n)更加接近的启发式函数。实际上我们可以设计一个更加tight的启发式函数，称为对角线启发式距离(Diagonal Heuristic)。

    下面是使用Diagonal Heuristic和欧式距离的结果对比：

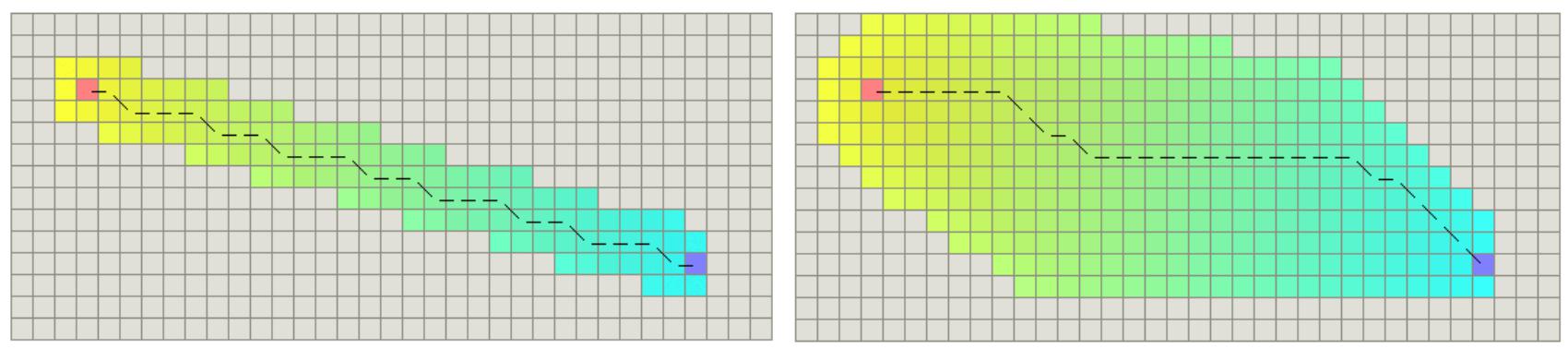
Tie Breaker

    对于基于栅格地图的图搜索问题来说，存在很多相同f(n)的路径，导致A*会拓展这些节点，导致计算资源的浪费。Tie Breaker的核心思想是在多个相同f(n)的路径中，根据某种倾向性来只选择一条进行拓展。

    第一种方法是轻微修改h(n)去打破不同路径的平衡性，即使得本来相同f(n)略微不同。比如h修改为：

    h=h*(1.0+p)

    p<(minimum cost of one step)/(expected maximum path cost)

    对h进行轻微放大可以减小这个问题，但同时也会影响h(n)的admissibility，虽然影响不大。下面是A*和带Tie Breaker的A*的比较：

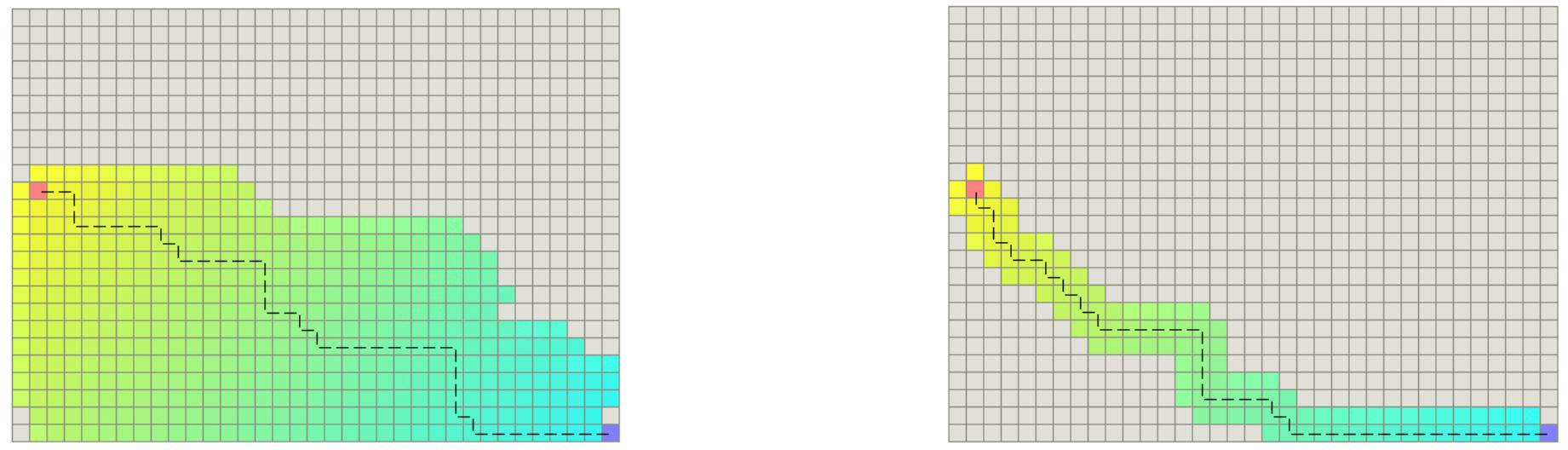
    第二种方法是对每个坐标预先设置一个随机数来打破这种平衡，这需要提前构建一个坐标的哈希表。

    第三种方法是显示给出一种方向倾向性，比如沿着到终点方向前进。比如可以增加一个额外的代价cross，表示节点n离起点到终点直线路径的偏移量，如下所示：

dx1=abs(node.x-goal.x)

dy1=abs(node.y-goal.y)

dx2=abs(start.x-goal.x)

dy2=abs(start.y-goal.y)

cross=abs(dx1*dy2-dx2*dy1)

h=h+cross*0.001

JPS算法

    JPS直接忽略掉路径中的对称性，只选择其中一条路径。JPS定义的拓展规则如下：

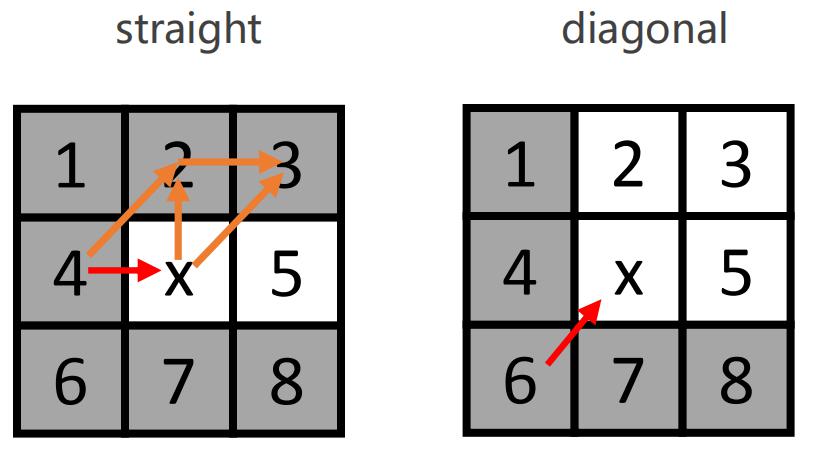
    白色节点称为自然邻节点，灰色节点称为较差邻节点。设计原则：如果邻节点可以通过x节点的父节点直接达到，并且花费的代价小于等于经过x节点达到的代价，那么该邻节点就无必要通过x节点到达。比如上图左的1号节点可以从x的父节点直接达到且代价为1，则x无需向1进行拓展。2号节点和3号节点同理。

    下面是存在障碍物的情况，黑色节点是障碍物节点，红色节点称为强制邻节点。

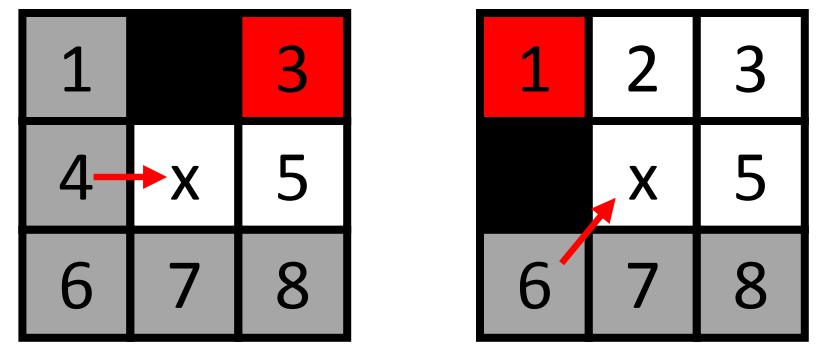
    下面是直线跳跃和对角跳跃的实例：

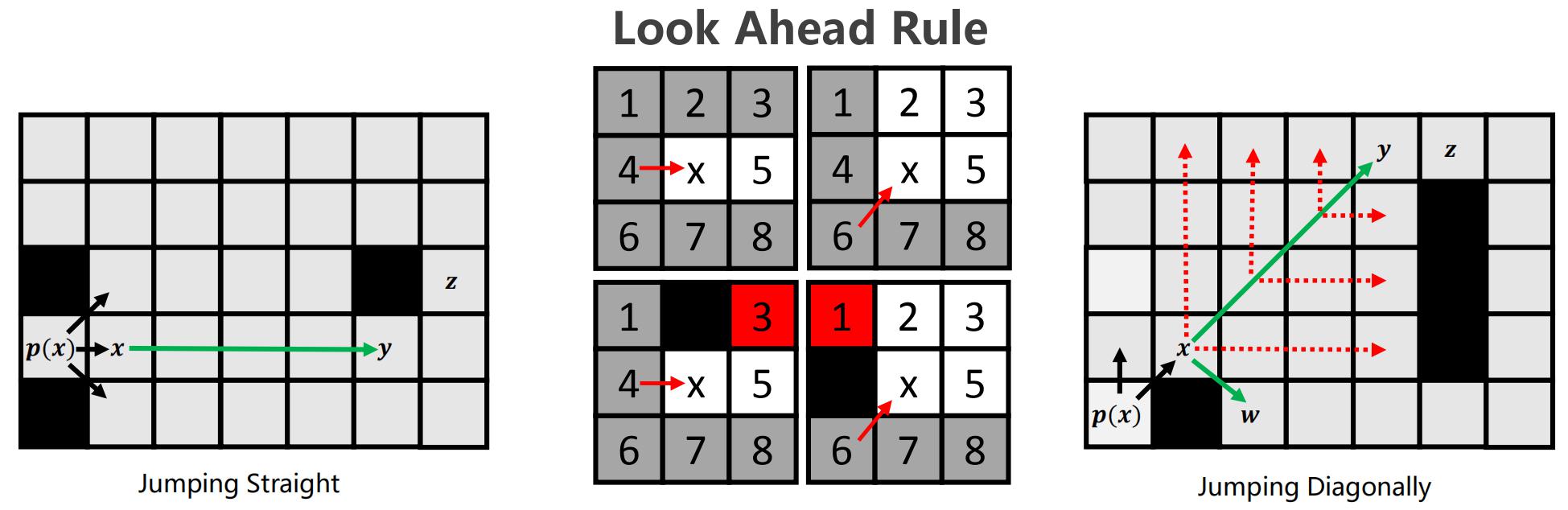
    对于直线跳越它会一直前进知道遇到force邻节点；对于对角线跳跃，它会在每个节点先进行直线跳跃，包括水平和竖直，然后再进行对角跳跃。

    满足条件：1.节点 x 是起点/终点；2.节点 x 至少有一个强制邻节点；3.父节点在斜方向（意味着这是斜向搜索），节点x的水平或垂直方向上有满足条件1，2的点，称为跳点。

    下面是一个更具体的例子：

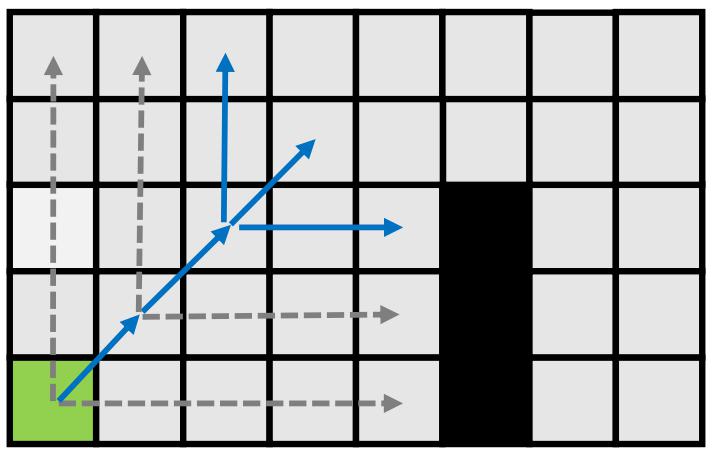
    从起点开始，首先沿着水平和垂直方向进行跳跃搜索，当遇到障碍物时结束搜索，若遇到强制邻节点则加入 openlist；然后再斜对角跳跃，直到遇到跳点。下面看到，当向右拓展时，发现了一个强制邻节点，将该邻节点放入open list中。

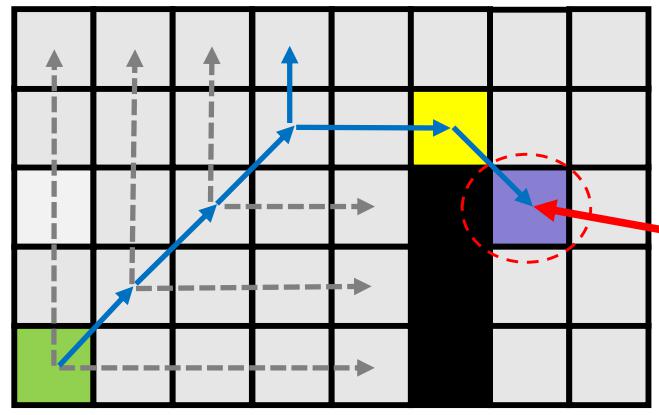
    JPS的算法流程总体与A*差不多，不同之处在于拓展节点的方法：

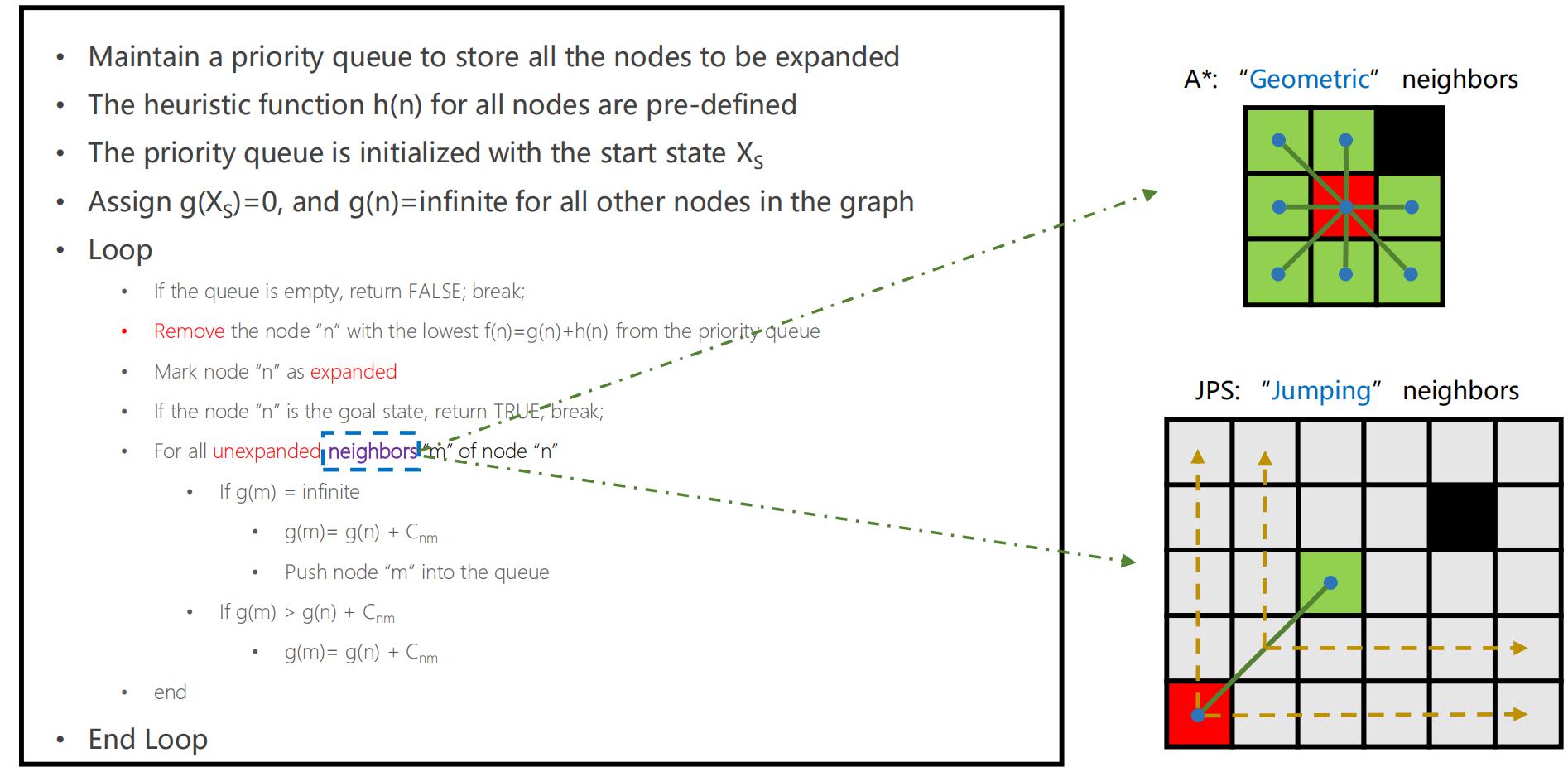
    1.openlist取一个权值最低的节点，然后开始搜索。（这些和A*是一样的）。

    2.搜索时，先进行 直线搜索（4/8个方向，跳跃搜索），然后再 斜向搜索（4个方向，只搜索一步）。如果期间某个方向搜索到跳点或者碰到障碍（或边界），则当前方向完成搜索，若有搜到跳点就添加进openlist。跳跃搜索是指沿直线方向一直搜下去（可能会搜到很多格），直到搜到跳点或者障碍（边界）。一开始从起点搜索，会有4个直线方向（上下左右），要是4个斜方向都前进了一步，此时直线方向会有8个。

    3.若斜方向没完成搜索，则斜方向前进一步，重复上述过程。因为直线方向是跳跃式搜索，所以总是能完成搜索。

    4.若所有方向已完成搜索，则认为当前节点搜索完毕，将当前节点移除于openlist，加入closelist。

    5.重复取openlist权值最低节点搜索，直到openlist为空或者找到终点。

然而JPS并不总是表现的很好，当整个地图中的障碍物区域很小时，JPS的性能可能弱于A*；而在复杂障碍物环境中，JPS的性能则远胜于A*。

代码实现

    A*在ROS中的实现：https://github.com/chenjianqu/Motion-Plan