强化学习笔记 experience replay 经验回放

UQI-LIUWJ

已于 2022-05-26 13:52:25 修改

阅读量7.5k

点赞数 12

分类专栏：强化学习文章标签：深度学习强化学习

于 2022-01-06 10:06:19 首次发布

本文链接：https://blog.csdn.net/qq_40206371/article/details/122336751

版权

强化学习专栏收录该内容

58 篇文章

订阅专栏

1 回顾：DQN

DQN 笔记 State-action Value Function(Q-function)_UQI-LIUWJ的博客-CSDN博客

DQN是希望通过神经网络来学习Q(s,a)的结果，我们输入一个人状态s，通过DQN可以得到各个action对应的Q(s,a)

通常用TD来求解DQN

其中rt是实际进行交互得到的真实奖励，Q(s,a), $Q(S_{t+1},a)$ 是预测得到的价值函数

(注：Q是fixed target network，所以qt和yt会稍有不同）

在之前我们所说的DQN中，我们每次采样得到一组episode $(s_t,a_t,r_t,s_{t+1})$ ，然后就用这组episode来计算相应的loss，进行梯度下降更新参数

而用这组数据训练了模型之后，这组数据就被丢弃了

2 TD算法的缺点

2.1 缺乏经验

而事实上，经验是可以重复使用的

2.2 correlated updates

比如玩游戏，当前画面和下一帧画面之间的区别会非常小，也就是 $s_t,s_{t+1}$ 会非常相近。实验证明把这些episode数据尽量打散，有利于训练得更好

另外一种思考的方式是，我每次更新DQN参数的时候，所需要的数据只是一个四元组 $(s_t,a_t,r_t,s_{t+1})$ ，与实际的策略 $\pi$ 关联不是很大，所以可以反复利用之前收集的实验四元组，来训练模型，更新参数

3 经验回放

经验回放可以克服之前的两个缺点

把最近的n条记录存到一个buffer里面

如果存满了，每次存入一条新的transition，就删除当前最老的那一条transition

需要人为指定replay buffer的大小b。即数组中只保存最近的b条数据。当replay buffer存满了之后，删除最旧的数据。

数组的大小b是一个需要调的超参数，大小会影响训练的结果。

在实践中，要等回放数组中有足够多的四元组时，才开始进行经验回放更新DQN

如果将DQN用于Atari游戏，最好收集了20万条四元组时再做经验回放，更新DQN
如果用更好的Rainbow DQN，收集了8万条四元组的时候就可以进行DQN的更新了

在回放数组中的四元组数量不够时，DQN只与环境进行交互，而不去更新DQN参数，否则实验效果会不好。

3.1 使用经验回放之后的TD

这里是从buffer中随机选择一个transition，实际上是从buffer中随机选择一个batch，做mini-batch SGD

3.2 经验回放的好处

1 打破了transition的关联性

在训练DQN的时候，我们希望相邻两次使用的四元组是独立的
但是智能体收集经验的时候，相邻的两个四元组和有很强的相关性。
- 依次使用这些强关联的四元组训练DQN，往往效果会很差。
经验回放每一次从数组里面随机抽取一个四元组，用来对DQN的参数进行一次更新。
- 这样随机抽到的四元组都是独立的，消除了其中的相关性。

2 经验可以重复使用

这样可以用更少的样本数量达到同样的表现

注意区分“样本数量”和“更新次数”，一个样本可以在不同的时候用来更新DQN参数

3.3 经验回放的局限性

并非所有的强化学习方法都允许重复使用过去的经验。
经验回放数组里的数据全都是用 行为策略 (Behavior Policy) 控制智能体收集到的。在收集经验同时，我们也在不断地改进策略。
- 策略的变化导致收集经验时用的 行为策略 是过时的策略，不同于当前我们想要更新的策略——即 目标策略 (Target Policy) 。
- 也就是说，经验回放数组中的经验通常是过时的行为策略收集的，而我们真正想要学的 目标策略不同于过时的行为策略。
有些强化学习方法允许 行为策略 不同于 目标策略 。这样的强化学习方法叫做 异策略

(Off-policy) 。【eg，Q-learning】
有些强化学习方法要求 行为策略 与 目标策略 必须相同。这样的强化学习方法叫做同

策略 (On-policy)。【eg，SARSA,A2C】——> 经验回放不适用于同策略。

4 优先经验回放

buffer里面有多条 transition，每条的优先级各不相同

它 比普通的经验回放效果更好 ：既能让收敛更快，也能让收敛时的平均回报更高。

比如以超级玛丽为例，左边是普通关卡，右边是打boss的关卡。左边常见右边不常见。由于右边的经验少，所以很难真正训练除右边的情况应该如何做决策，在这种情况下，右边的重要性更大一些。

4.1 如何判断哪些样本重要？

那么如何自动判断那些样本更重要呢？

比如boss关卡数量少，这就导致DQN的预测值 $Q(s_j,a_j;w)$ 严重偏离 $Q_*(s_j,a_j)$

因此，要是 $|Q(s_j,a_j;w)-Q_*(s_j,a_j)|$ 较大，那么应该给样本 $(s_j,a_j,r_j,s_{j+1})$ 较高的权重。

在实操中 $Q_*(s_j,a_j)$ 是未知的，所以我们可以用TD来近似表示之

如果TD误差的绝对值 $|\delta_j|$ 大，说明当前的DQN对 $(s_j,a_j)$ 的估计不准确，那么应该给样本 $(s_j,a_j,r_j,s_{j+1})$ 设置较大的权重。

在priority experience replay 中，如果一条transition有更高的TD error δt，那么我们就认为他距离TD target比较大，DQN就不熟悉这个场景，所以需要给他较大的优先级。

4.2 如何设置采样概率？

优先经验回放的思路就是用非均匀抽样代替均匀抽样，有两种抽样方法

option 1 中的ε是一个很小的数，为了防止抽样概率接近于0
rank(t)是δt排序后的序号，δt越大，rank(t)越小

——>两种option的原理是一样的：TD误差大的样本被抽样道德概率大

4.3 如何调整学习率？

        抽样的时候是非均匀采样的，我们需要相应地调整学习率，以减少不同抽样概率带来的偏差



        如果一条transition有较大的抽样概率，那么他的学习率应当相应地小一些（用来抵消大抽样概率带来的偏差，因为大抽样概率那么我被采样到的次数就会稍多）

n是经验回放数组中样本的总数
p是采样样本 $(s_j,a_j,r_j,s_{j+1})$ 的概率
β是一个需要调的超参数
【其实均匀抽样可以看成一个特例】

4.3.1 学习率和抽样概率互相抵消了嘛？

当β=1时，如果抽样概率p增大10倍，但是学习率α缩小10倍，那么抽样概率和学习率不是抵销了嘛？

其实不是的，下面两种方式并不等价

乍看起来两种方式区别不大，但其实第二种方式是对样本更有效的利用。

第二种方式的缺点在于计算量大了十倍；所以第二种方式只被用于重要的样本。

如果一条transition 刚被采集到，我们是不知道他的δt的，此时我们直接给他设置最大的优先级，也就是未被使用过的transition具有最高的优先级

每次使用一条transition之后，我们都要重新更新他的δt

4.3.2 总体流程

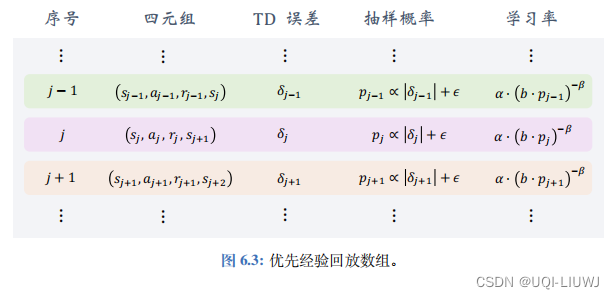
优先经验回放数组如图 6.3 所示。设 b 为数组大小，需要手动调整。
如果样本（即四元组）的数量超过了 b，那么要删除最旧的样本。
数组里记录了四元组、 TD 误差、抽样概率、以及学习率。
注意，数组里存的 TD 误差 δ j 是用过时 DQN 参数计算出来的（这也影响到抽样概率和学习率）：
做经验回放的时候，每次取出一个（或多个）四元组，用它计算出新的 TD 误差：
- 然后用它更新 DQN 的参数。用这个新的 δ′j 取代数组中旧的 δj。（抽样概率和学习率也同步更新）