强化学习笔记：对决网略（dueling network）

对决网络 (Dueling Network) 是对 DQN 的神经网络的结构的改进。

它基本想法是将最优动作价值 Q ⋆ 分解成最优状态价值 V ⋆ 与最优优势 D ⋆ 。

1 最优优势函数

1.1 回顾一些基础知识

•  动作价值函数

• 最优动作价值

• 状态价值函数：Q(s,a)关于a的期望

  

  • 最优价值函数

   
  
  
   

1.2 最优优势函数

        由于 是指定了s和a之后的最优值，a不一定是使得V(s)最大的那个action，所以

        也就是说，  （a为使得V(s)最大的那个action时，取到这个max）

 

 

2 对决网络

•  与 DQN 一样，对决网络 (Dueling Network) 也是对最优动作价值函数 Q⋆ 的近似。
• 对 决网络与 DQN 的区别在于神经网络结构不同。
• 由于对决网络与 DQN 都是对 Q⋆ 的近似， 可以用完全相同的算法训练他们。

• 对决网络由两个神经网络组成
  • 一个神经网络记作，它是对最优优势函数的近似
  • 另一个神经网络记作，它是对最优价值函数V*(s)的近似

 

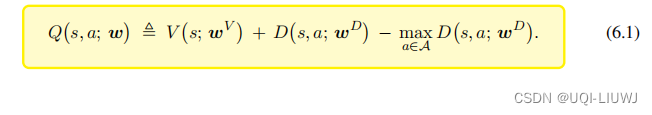
注：这里右边的第三项不一定恒为0，因为神经网络D是近似D*，而不是真的等于D*，如果等于的话，那第三项是0。 

2.1 对决网络举例

举个例子，动作空间是 A = { 左 , 右 , 上 } ，优势头的输出是三个值：

状态头 输出的是一个实数，比如是：

 首先计算

 然后用(6.1)计算出

 这个就是对决网络的最终输出

 3 为什么公式的最后一项必须要

由于对决网络是由定理6.1 推导出的

 那么最优动作价值就可以有两种等价形式

 那么能不能用第一种形式实现对决网络呢？

 

答案是不可以，因为这样会导致不唯一性

假如这样实现对决网络，那么 V 和 D 可以随意上下波动，比如一个增大 100 ，另一个减小 100 ：

这样的上下波动不影响最终的输出：

 

这就意味着 V 和 D 的参数可以很随意地变化，却不会影响输出的 Q 。我们不希望这种情

况出现，因为这会导致训练的过程中参数不稳定。

 因此很有必要在对决网络中加入 第三项，他使得V和D不能随意地上下波动

假如让 V 变大 100 ，让 D 变小 100 ，则对决网络的输出会增大 100 ，而非不变：

 

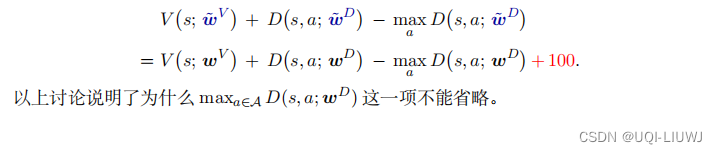
4 对决网络的实际实现

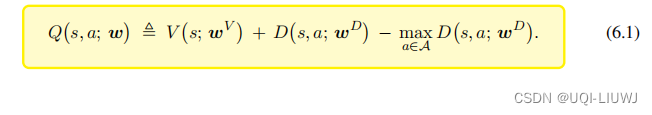
在实际实现的时候，用mean代替max会有更好的效果

所以我们实际上这么实现对决网络

 

• 对决网络与 DQN 都是对最优动作价值函数 Q⋆ 的近似，所以对决网络与 DQN 的训练和决策是完全一样的。
  • ​​​​​​​怎么样训练 DQN，就怎么样训练对决网络；
  • 怎么样用 DQN 做控制，就怎么样用对决网络做控制。
  • 如果一个技巧能改进 DQN 的训练，这个技巧也能改进对决网络。
  • wgtrf同样的道理，Q 学习算法导致 DQN 出现高估，同样也会导致对决网络出现高估。