2020 Neurips
1 intro & abstract
- 视频表征的一个挑战是高维、动态、各个像素之间多模态分布
- 最近的一些研究通过探索视频的inductive bias,并将高维数据映射到低微数据中
- —>这种方法通过将视频的各帧分解成语义上有意义的因子,来获得视频的解耦表征
- ——>但是,当物体在视频中有缺失时,现存的方法并不能很好地进行建模
- 这篇论文就希望学习 带有缺失数据的视频的解耦表征
- 提出了DIVE (disentangled-imputed-video autoencoder)
- 通过将视频分解成appearance、pose和missingness 这三个隐变量,来学习视频的表征
- 通过学习到的解耦隐变量,来补全视频中的缺失数据
- 使用补全了的视频表征进行随机的、无监督的视频预测
- 提出了DIVE (disentangled-imputed-video autoencoder)
2 related work
2.1 解耦表征
- 序列的无监督学习解耦表征通常有三类
| 基于VAE的 |
|
| 基于GAN的 |
|
| 基于加&乘的 |
|
- 对于视频数据而言,最常用的做法是将视频帧编码成隐变量,然后将隐藏表征分解成内容和动态因子(content,dynamics)
- 视频中的内容(物体、背景。。。)是固定的
- 视频中物体的方位则会一直改变
- ——>但大部分模型只能解决没有缺失数据的视频
2.2 视频预测
- 视频预测一般是基于过去的视频帧来预测未来的视频帧
- 使用LSTM,ConvLSTM,PredRNN等模型
- 但这些模型的问题是,他们预测的都是确定值(帧),这并不能很好地建模视频数据中未来帧的不确定性
- 论文中使用随机视频预测,这能更好地捕获环境中的随机动力学
3 Disentangled-Imputed-Video-autoEncoder (DIVE)
- 在这篇论文中,作者假设每一个视频最多有N个物体;观测K个时间片的视频序列,预测K+1~T的视频帧
- 模型整体上是一个VAE架构,将视频中的物体分解成三种不同的隐变量:appearance、pose、missingness
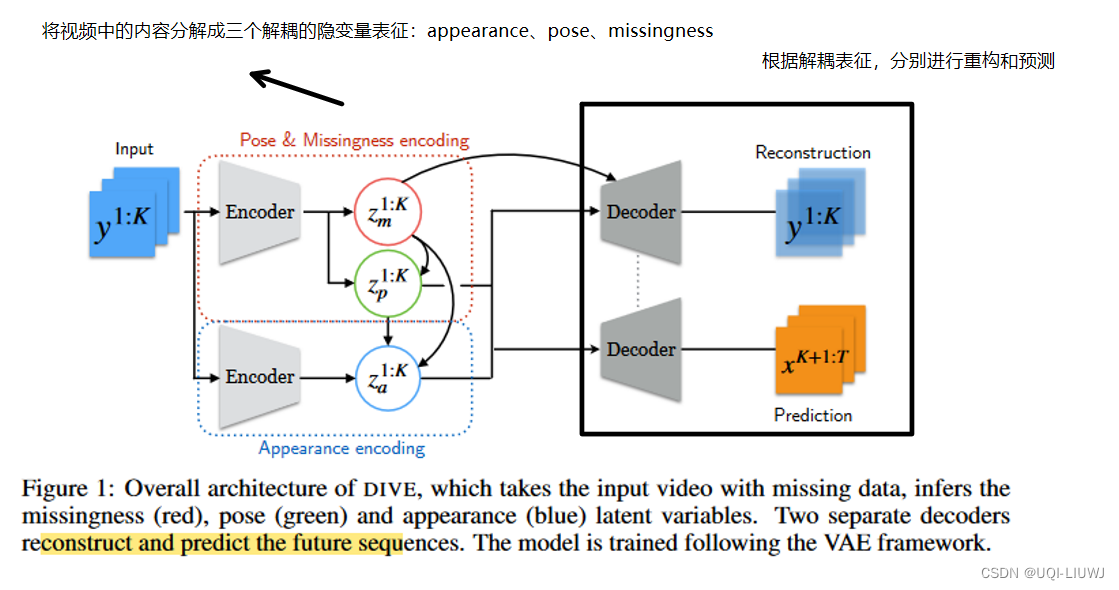
- 记带缺失数据的视频为
,其中每一个
是一帧
- 论文旨在学习视频的隐藏表征
,并将其解耦成三个不同的隐变量
- i表示视频的第i个物体
表示h维的appearance向量
是一个三维的向量,表示pose(x,y坐标和缩放大小)
是0/1的missingness 标签(1表示物体被遮住/丢失)
- 论文旨在学习视频的隐藏表征
3.1 补全模型
- 补全模型根据missingness标签
来更新隐藏状态
- 如果没有丢失数据,那么补全模型的隐藏状态更新方式为:
- 这里
是双向LSTM
- i-1是上一个物体(但是视频里面物体怎么排序,我好像在这篇论文里没有找到,熟悉这一领域的欢迎补充)
- 这里
- 如果有缺失值的话
中yt是得不到的,故而需要补全,记此时需要补全的内容的隐藏状态为
- FC是全连接层,
是这一小节要介绍的pose的隐藏状态
- FC是全连接层,
- 记隐藏层的向量为
,他回根据不同的 missingness标签
来选择不同的隐藏状态
- 这里当没有丢失数据的时候,这边使用的是
的混合,论文发现这样效果更好
- 输入只是带缺失值的y,所以我们并不能直接知道missingness标签
,这个值到底是0还是1,是通过后面的3.2.1 missingness inference得到的
- pose的隐藏状态
通过LSTM来更新
3.2 推断模型
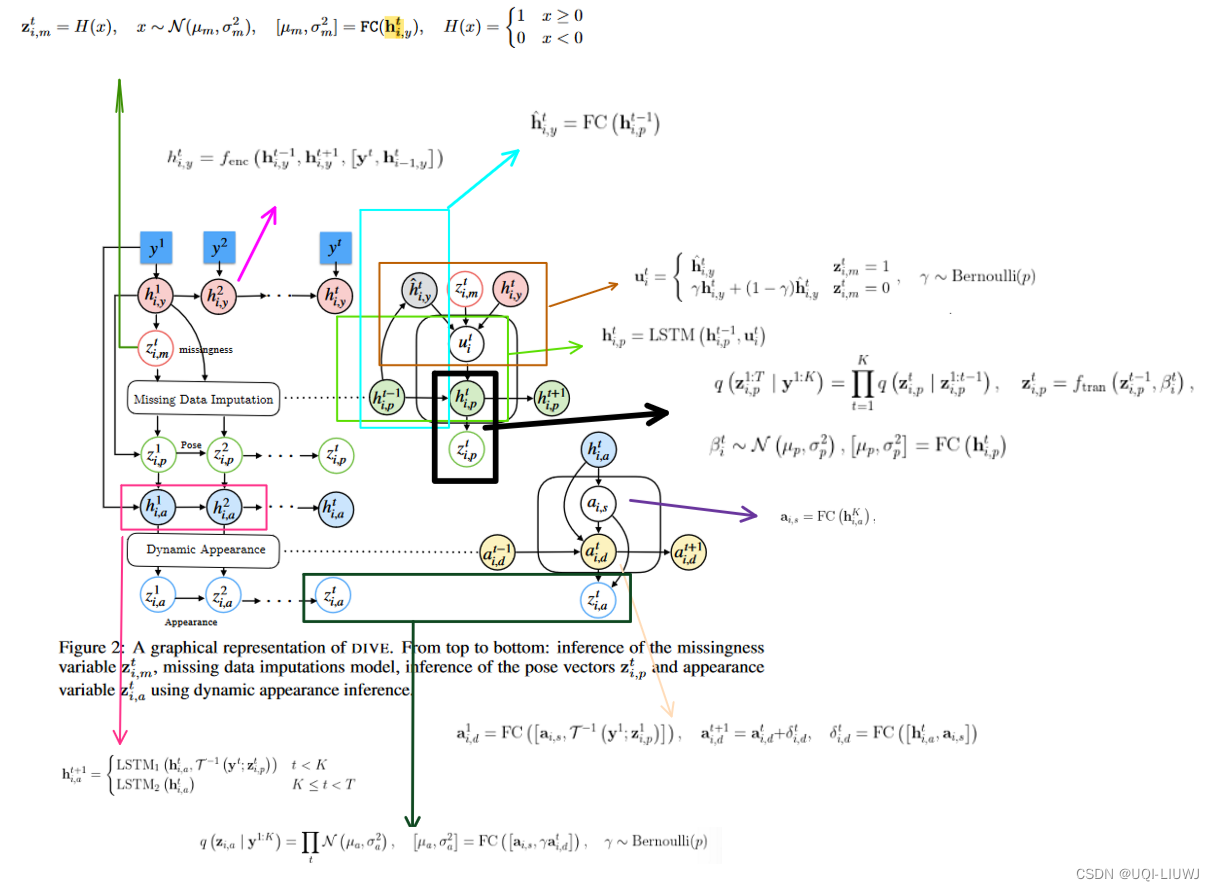
一开始我们只有视频数据y,怎么得到z呢
3.2.1 missingness inference
- 对于missingness变量
,使用如下的方式推断
3.2.2 pose inference
3.2.3 dynamic appearance
- appearance变量
是一个随时间一直变化的内容
- 论文这里把appearance分解成静态分量
和动态分量
- 论文这里把appearance分解成静态分量
- 对于静态分量,作者使用“Learning to decompose and disentangle representations for video prediction.”中的inverse affine spatial transformation
- (对未来视频的预测,就是一种自回归的方式了(t的hidden state是t+1的input)
- 对于动态分量,作者建模的是各帧之间的区别
- 最后的appearance是将动态和静态结合在一块得到的
3.4 生成模型与学习
- 给定带有丢失数据的视频
,记潜在的完整视频为
,那么,视频序列的生成概率分布为:
- 其中每一个object的概率可以用如下方式计算而得
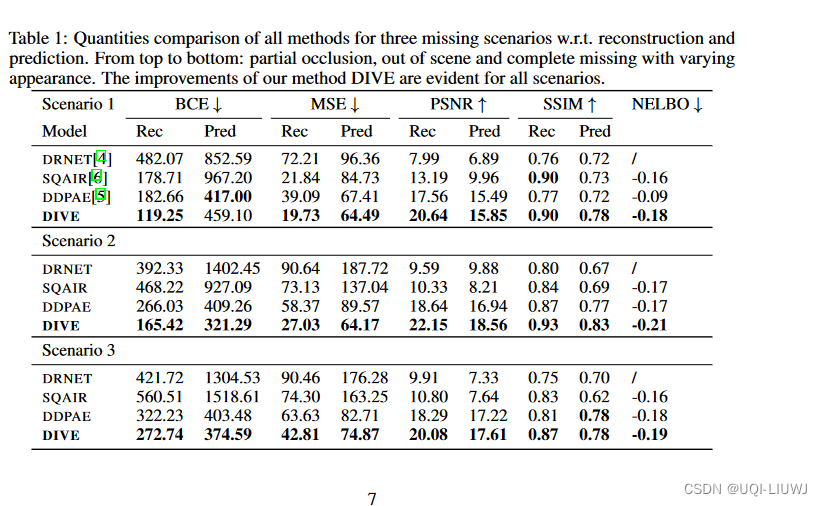
4 实验部分
- 给定10帧,预测10帧
























 1462
1462











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










