智能驾驶横向控制算法之PID

1.PID简介

        PID是一种不依赖系统模型的控制算法，由于其算法简单，鲁棒性好和可靠性高，被广泛应用于工业过程控制。在工程实际中，当被控对象的结构和参数不能完全掌握，或得不到精确的数学模型时，这时应用PID控制器最为方便。PID控制器就是根据系统的误差，利用比例、积分、微分计算出控制量进行控制的。

连续控制系统的理想PID控制规律为：

线性控制规律为：

其中：

        Kp为比例增益

        Ti为积分时间常数

        Td为微分时间常数

        u(t)为PID控制器的输出信号

        e(t)为给定值与测量值的偏差

具体的流程图可表示为：

2.PID基本原理

(1)比例环节P

        成比例地反映控制系统的偏差信号，偏差一旦产生，立即产生控制作用以减小偏差。比例控制器的输出u(t)与输入偏差e(t)成正比，能迅速反映偏差，从而减小偏差，但不能消除静态偏差。

        静态偏差是指系统控制过程趋于稳定时，给定值与输出量的实测值之差。偏差存在，才能使控制器维持一定的控制量输出，因此比例控制器必然存在着静差。由偏差理论可知，增大P虽然可以减小偏差，但不能彻底消除偏差。

        比例控制作用的大小除与偏差e(t)有关之外，还取决于比例系数Kp的大小。比例系数Kp越小，控制作用越小，系统响应越慢；反之，比例系数Kp越大，控制作用也越强，则系统响应越快。但是，Kp过大会使系统产生较大的超调和振荡，导致系统的稳定性能变差。因此，不能将Kp选取过大，应根据被控对象的特性来折中选取Kp，使系统的静差控制在允许的范围内，同时又具有较快的响应速度。由下图可知，太大的Kp导致系统产生较大的震荡。

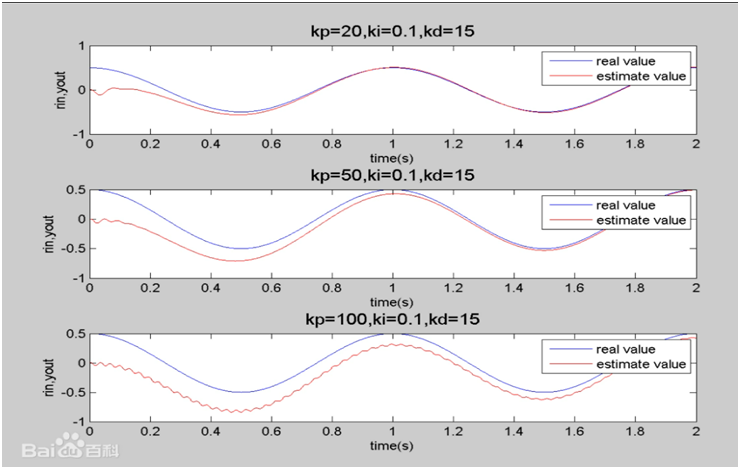
（2）积分环节

        积分环节的作用，主要用于消除稳态误差，提高系统的无差度。积分作用的强弱，取决于积分时间常数Ti，Ti越大积分作用越弱，反之则越强。积分控制作用的存在与偏差e(t)的存在时间有关，只要系统存在着偏差，积分环节就会不断起作用，对输入偏差进行