相对收益-权益类组合归因-Brinson 绩效归因模型

周纠纠

已于 2025-02-10 23:32:54 修改

阅读量1.1k

点赞数 16

分类专栏： # 金融分析笔记文章标签：线性代数

于 2025-02-07 23:34:53 首次发布

本文链接：https://blog.csdn.net/qq_40947195/article/details/145503845

版权

金融分析笔记专栏收录该内容

12 篇文章

订阅专栏

Brinson 绩效归因模型

1、前言
2、Brinson模型介绍
3 案例
- 3.1 简单案例
总结

1、前言

如此之多的基金，收益率各有不同，即使同等收益率的基金也各有不同的成因。在这种形势下，广大投资者需要对基金的投资业绩进行合理的归因，并据此判断基金业绩将持续或是反转，从而做出科学的投资决策。

基金业绩归因分析主要分为两种：

一种是基于收益率的时间序列回归法，包括H-M模型、C-L模型等；
一种是基于持仓数据的归因分析，包括风格因子、Brinson模型等。

2、Brinson模型介绍

Brinson模型是由1986年的一篇论文提出的，该论文的作者是Brinson, Hood和 Beebower，因而也叫做BHB模型。该模型背后的假设是：股票基金经理仅投资于国内的股票市场，并且一直满仓，采取自上而下的投资方法，进行宏观研究、行业研究、个股研究后，先进行行业配置，然后再在各行业中选取个股。

Brinson 模型是一种基于持仓数据对基金业绩进行归因的工具，能够对单期或多期的基金超额收益来源进行详细分解。它通过分析基金具体的持仓信息，将基金当期的收益分解为不同的效应，从而对组合的损益来源有更明确的认识。

2.1 归因方式

Brinson 归因方式主要包括 BF 方案和 BHB 方案，它们分别提出了不同的收益分解方式。
在这里插入图片描述

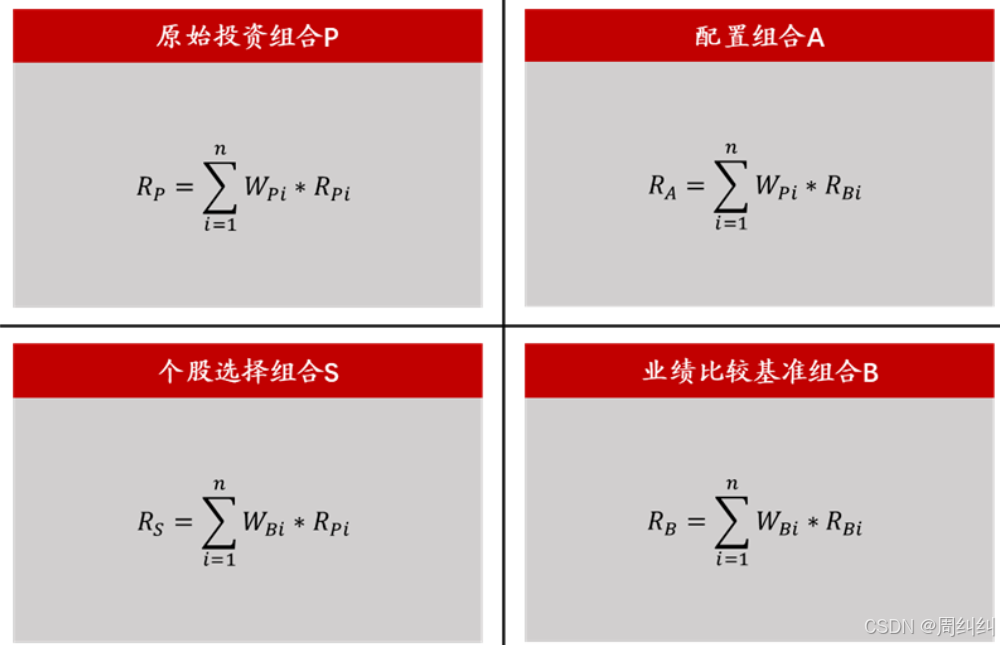
构建的四个投资组合

在这里插入图片描述

我们可以用图形来更直观地展示 BF 和 BHB 方案的收益分解方式。下图白色部分代表了基准组合的收益，彩色部分代表了基金组合相对于基准的超额收益。

2.1.1 BHB 超额收益分解方案

1986 年，Brinson、Hood 和 Beebower 提出了另一种基于 Brinson 模型的超额收益拆分方案，简称为 “BHB 方案”。

这一方案在业界应用广泛。BHB 方案通过构建两个虚拟组合——资产配置组合和标的选择组合，将基金组合的超额收益分解为三个部分：

配置收益（Allocation Return, AR）：定义为策略组合在不同资产类别上相对基准的权重偏离带来的超额收益，即假设策略组合和基准指数中的各类资产的收益不变，策略组合中资产类别的配置权重和指数中资产权重不同带来的收益差异。配置收益衡量基金经理在不同资产类别或行业之间进行资产配置的能力。它反映了基金经理通过选择不同资产类别或行业的权重来超越基准的能力。
选择收益（Selection Return, SR）：定义为策略组合在不同资产类别上相对基准的收益能力差异带来的超额收益，即假设策略组合和基准指数中的各类资产的权重不变，策略组合中资产类别的收益率和指数中该类资产收益率不同带来的收益差异。选择收益衡量基金经理在具体标的选择上的能力。它反映了基金经理选择的个股或债券在相对于基准组合的超额收益。
交互收益（Interaction Return, IR）：定义为超额收益中无法用上述两种贡献解释的部分，它是由配置和选券共同作用的。交互收益反映了资产配置和标的选择之间的交互效应。它表示由于资产配置和标的选择共同作用而产生的超额收益。交互效应本身并不具有单独的经济含义，也不是投资决策流程的一部分，因此很难对交互效应本身的计算结果提出要求，或寻找有擅长创造交互效应贡献的基金经理。

超额收益
$=\sum_{i=1}^{n} \omega_i^PR_i^P-\sum_{i=1}^{n} \omega_i^BR_i^B \\=AR+SR+IR \\=\sum_{i=1}^{n} (\omega_i^P-\omega_i^B)R_i^B +\sum_{i=1}^{n} (R_i^P-R_i^B)\omega_i^B +\sum_{i=1}^{n} (R_i^P-R_i^B)(\omega_i^P-\omega_i^B)$

即：

配置效应=组合超额权重*组合基准资产收益率
选择效应=基准权重*组合超额收益率
交叉效应=组合超额权重*组合超额收益率

BHB模型的缺陷：

强调超额配置收益来源于对上涨行业的超配或者对下跌板块的低配，适合考虑绝对收益的投资组合，但是在普遍上涨的行业中，BHB要求对所有上涨的行业都需要进行超配，这显然是做不到的。
因为在实际投资中，当超配一个行业时，必将以另一行业的低配为代价，同时，对于组合来说，板块好坏的判断标准应该是板块能都取得比基准更好的表现，而不是这个板块的绝对收益。
因此，需要对BHB模型进行改写，由此得出了BF模型；

$r^B$ 代表：投资基准组合的收益；

$r_i^B$ 代表：投资基准组合在 $i$ 板块的收益

$r_i^B-r^B$ 代表：投资基准组合在 $i$ 板块相对于基准组合整体收益的一个变化

强调超额配置收益来源于对涨幅超过基准总收益的行业的超配或者对跌幅超过基准总收益的行业的低配；
比较适合于相对收益的投资组合

2.1.2 BF 超额收益分解方案

在1985年，Brinson 和 Fachler 提出了一个收益分解方案，简称为 “BF 方案”。

与 BHB 方案不同，BF 方案没有包含交互收益，而是将其并入了选择收益当中。
因此，BF 方案仅有两个部分：

配置收益（Allocation Return, AR）：配置收益的定义与 BHB 方案相同，但 BF 方案引入了基准组合的收益率，衡量基金经理在资产配置上的能力。
选择收益（Selection Return, SR）：在 BF 方案中，选择收益不仅衡量基金经理在具体标的选择上的能力，还包括了交互效应。因此，选择收益反映了基金经理在标的选择和资产配置共同作用下的综合超额收益。

BHB方案本身有如下缺陷：
在这里插入图片描述

2.2 多期 Brinson 模型

多期 Brinson 模型与单期 Brinson 模型的主要区别在于对持仓变化和再投资收益的处理方式上。

单期 Brinson 模型假定在样本期内基金经理没有调仓，组合没有现金流入和流出，因此其适用范围局限于单个时间段内的绩效分析。然而，对于一个组合较长时间段内的收益分析，尤其是在组合持仓发生较大变化的情况下，单期 Brinson 模型的基本假设就不再适用。

因此，多期 Brinson 模型的基本原理是将较长时期划分为多个单期，在每个单期内假设持仓保持不变并进行收益归因，最后将各个单期的归因结果进行合理加总，得到整个时期的绩效归因结果。

基准组合 $t$ 期收益： $R_t^B=\sum_{i=1}^{n} \omega_{i,t}^BR_{i,t}^B$

资产组合 $t$ 期收益： $R_t^P=\sum_{i=1}^{n} \omega_{i,t}^PR_{i,t}^P$

基准组合累计收益： $R^P=\prod_{t=1}^{T}(1+R_t^P)-1$

资产组合累计收益： $R^B=\prod_{t=1}^{T}(1+R_t^B)-1$

$R_{i,t}^B$ ： $t$ 时刻， $i$ 板块的收益；

$R_t^B$ ： $t$ 时刻，组合的收益；

$R^B$ ：组合在期间的累计收益

然而多期模型的归因结果不能直接将各个单期的收益进行简单相加，这是因为超额收益

在这里插入图片描述

显然，若超额收益不能简单相加，绩效归因的结果也不能简单相加。这是因为其中存在再投资收益。而同时，因为我们有时也需要得到各个单期的归因结果，不能仅仅停留在简单的累乘相减得到总的归因情况。为此，比较典型、简单的就有如下算法：

2.2.1 Carino算法

该算法主要是克服了多期绩效归因中不能直接简单相加的缺点，利用对数形式将上述结果进行了一定的数学转化。考虑到
$\ln(1+R)=\ln(1+\prod_{t=1}^{T}(1+R_t)-1)=\ln\prod_{t=1}^{T}(1+R_t)=\sum_{t=1}^{T}\ln(1+R_t)$

对于多期超额收益有：
在这里插入图片描述
整理后便有：

在这里插入图片描述
若要查看多期模型下单期的归因，只需在单期模型的归因结果中，乘上对应的修正因子 $\alpha_t=k_t/k$ 即可。然而，这种方法的提出本质上只是通过简单的代数运算，正确计算出了多期的总体绩效归因，对于t期超额收益后续在基准指数上的再投资收益的归属尚不明确， $ER (t)$ 等的计算方式还有待商榷。

2.2.2 GRAP算法

解决Carino算法问题的有两种算法，一是Frongello算法，二是GRAP算法。
二者区别在于，Frongello算法将 $i$ 期的超额收益于 $j$ 期在基础资产上的再投资收益归因到了 $j$ 期，GRAP算法将 $i$ 期的超额收益于 $j$ 期在基础资产上的再投资收益归因到了 $i$ 期。

本文介绍后者，这是因为再投资本身相当于一种选择，超额收益的再投资收益本身相当于把超额收益重新放入策略中的回报。尽管随着时间推移，GRAP算法每次总是要重新进行归因，但这种方式使得每期超额收益组成更合理，归因结果相对更为可靠。

GRAP 算法的核心理念是将再投资收益归属到超额收益产生阶段，而非再投资收益的实际发生阶段，以确保修正后的各单期配置收益和选择收益能够直接相加，获得全样本期的绩效归因结果。

计算方法如下：首先还是在单期框架下计算相应的归因结果 $ER_t$ 、 $AR_t$ 、 $SR_t$ ； ,随后根据GRAP算法的原理，第t期的超额收益 $ER （ t ）$ 应该由两部分组成：

$1$ _{$t-1$的累计净值在$t$期所产生的超额收益$+t$期超额收益在$t+1$} $T$ 期于基准指数上产生的在投资收益，即有

针对多期 Brinson 模型的算法设计，专家学者们提出了各种收益修正算法。为了将后续的再投资收益纳入考虑，此模型运用了 GRAP 算法。GRAP 算法的核心理念是将再投资收益归属到超额收益产生阶段，而非再投资收益的实际发生阶段，以确保修正后的各单期配置收益和选择收益能够直接相加，获得全样本期的绩效归因结果。因此，GRAP 算法中 n 期的多期超额收益 ER(n) 变为：

2.3 资产维度的 Brinson 模型

除了行业维度，还可以做资产大类维度的Brinson 模型

3 案例

3.1 简单案例

假设一个基金经理采用杠铃策略，在今年年初构建了投资组合P：分别将70%、20%、10%的资产投资于煤炭、传媒、汽车行业，并通过精选个股，分别在三个行业获得了12%、-5%、-2%的归一化收益率。（归一化收益率指的是，假设满仓将获得的收益率。例如，12%的仓位在行业A获得了1%的收益率，则归一化收益率为12%。）将该基金的业绩比较基准设为B，其中B由50%的煤炭行业和50%的传媒行业组成，年初至今（3月27日），煤炭行业和传媒行业的收益率分别为8.19%和5.63%。

此时该如何使用Brinson模型进行绩效归因？只需要将基准组合中汽车的权重视为0即可。Brinson模型的应用过程及结果如下图所示：
在这里插入图片描述
当沪深300指数为基准组合时

大部分时候，一只基金的业绩比较基准组合里面不会只有煤炭行业和传媒行业，更常用的是沪深300指数等宽基指数。假设基金仍投资于煤炭、传媒、汽车行业，权重和归一化收益率不变，我们以沪深300指数为业绩比较基准，再使用Brinson模型进行绩效归因，过程及结果如下图所示：
投资组合P的收益拆分
在这里插入图片描述
投资组合B的收益拆分

在这里插入图片描述
通过Brinson模型的运行结果，我们得出该基金相比沪深300指数获得了较高的超额收益，具体来看：行业配置收益为1.24%，贡献不多，说明单纯行业层面的选择并未创造较高收益；个股选择收益为5.99%，说明在个股的选择上比较有效；交叉收益为5.83%，配置和个股选择的协同效应也较高。