Vslam14讲(复习三)

三维空间刚体运动

主要目标:

1. 理解三维空间的刚体运动描述方式：旋转矩阵、变换矩阵、四元数和欧拉角。
2. 掌握Eigen库的矩阵、几何模块的使用方法。

视觉SLAM的基本问题之一：如何描述刚体在三维空间中的运动。直观上看，一次旋转加一次平移确实没多大问题，但是旋转的处理比较麻烦。所以引入了旋转矩阵、四元数、欧拉角等定义，以及它们是如何运算的。Eigen是一个优秀的库，这一讲将重点实现和运用下。

3.1 旋转矩阵

3.1.1 点、向量、坐标系

三维空间由三个周轴组成，所以一个空间点的位置可以由三个坐标指定。当考虑刚体时，就不光有位置，还有刚体的自身姿态。。相机也可以看成三维空间的刚体，于是位置是指相机在空间的那个地方，而位姿则是相机的朝向。我们考虑用数学语言来描述。

从最基本的内容谈起：点和向量。点就是空间的基本元素，没有长度，没有体积。把两个点连接起来，就构成了向量。向量可以看成，从某点指向另一个点的箭头。

向量的外积是重点：如下，会引入新的概念

另外，向量和反对称矩阵是一一映射的。

3.1.2 坐标系间的欧式变换

相机视野中的某个向量p，它在相机坐标系下的坐标为pc，而从世界坐标系下看，它的坐标为pw。那么两个坐标之间是如何转换的呢？

这时，我们需要先得到该点针对机器人坐标系的坐标值，再根据机器人位姿变换到世界坐标系下。我们需要用一种数学手段来描述这个变换，可以用一个矩阵T来描述它。

两个坐标系之间的运动可以用一个旋转加上一个平移组成，这种运动称为刚体运动。相机运动就是一个典型的刚体运动。

手机坐标系到世界坐标系之间，差了一个欧式变换。看下图：

 

欧式变换由旋转和平移组成。首先考虑旋转。设某个单位正交基(e1,e2,e3)经过一次旋转变成了(e'1,e'2,e'3)。那么，对于同一个向量a(设该向量始终未动)。它在两个坐标系下的坐标为[a1,a2,a3]T,[a'1,a'2,a'3]T,因为向量本身没变，所以根据坐标系的定义，有(从空间上理解一下)：

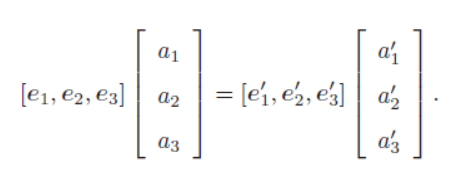
旋转矩阵有一些性质：

1. 它是一个行列式为1的正交矩阵。同时行列式为1的正交矩阵也是旋转矩阵。n维旋转矩阵的集合定义如下：

下面这个要重点理解：

3.1.3 变换矩阵与齐次坐标

齐次坐标的引入比较简单，掠过。

回想下多视图几何里面的内容吧。

3.2 实践Eigen

Eigen的安装略过，建议源码安装。

注意：Eigen头文件默认位置在“/usr/include/eigen3”.

与其他库相比，Eigen的特殊之处在于，它是一个纯用头文件搭建起来的库。所以只能找到它的头文件，找不到.so或者.a的二进制文件。在使用时，只需要引入Eigen的头文件即可，不需要链接库文件(因为没有库文件)

下面进行代码练习：

#include <iostream>
using namespace std;

#include <ctime>

//Eigen核心部分
#include <Eigen/Core>
//稠密矩阵的代数运算(逆、特征值)
#include <Eigen/Dense>
using namespace Eigen;

#define MATRIX_SIZE 50

/**********本程序演示Eigen基本类型的使用************/


int main()
{
//Eigen中所有向量和矩阵都是Eigen::Matrix,它是一个模板类。它的前三个参数为数据类型、行、列
//声明一个2*3的float矩阵
Matrix<float,2,3> matrix_23;

//同时，Eigen通过typedef提供了许多内置类型，不过底层仍是Eigen::Matrix
//例如，Vector3d实质上是Eigen::Matrix<double,3,1>,即三维向量
Vector3d v_3d;
//这是一样的
Matrix<float,3,1> vd_3d;

//Matrix3d实质上是Eigen::Matrix<double,3,3> 
Matrix3d matrix_33 = Matrix3d::Zero(); //初始化为零
//如果不确定矩阵大小，可以使用动态大小矩阵
Matrix<double,Dynamic,Dynamic> matrix_dynamic;
//更简单的
MatrixXd matrix_x;
//这种类型还有很多，不一一举例

//下面是对Eigen阵的操作
//输入数据(初始化)
matrix_23<<1,2,3,4,5,6;
//输出
cout<<"matrix 2x3 from 1 to 6: \n"<<matrix_23<<endl;

//用()访问矩阵中的元素
cout<<"print matrix 2x3: "<<endl;
for (int i = 0;i < 2;i++)
{
for (int j = 0;j < 3;j++)
cout<<matrix_23(i,j)<<"\t"<<endl;
}

//矩阵和向量相乘(本质上仍然是矩阵和矩阵相乘)
v_3d<<3,2,1;
vd_3d<<4,5,6;

//但是Eigen中不能混合两种不同类型的矩阵，像下面这样就是错的
//Matrix<double,2,1> result_wrong_type = matrix_23*v_3d;
//应该显示转换为
Matrix<double,2,1> result = matrix_23.cast<double>()*v_3d;
cout<<"[1,2,3;4,5,6]*[3,2,1]="<<result.transpose()<<endl;

Matrix<float,2,1> result2 = matrix_23*vd_3d;
cout<<"[1,2,3;4,5,6]*[4,5,6]="<<result2.transpose()<<endl;

//同样，不能搞错矩阵的维度
//试着取消下面的注释看看后果
//Eigen::Matrix<double,2,3> result_wrong_dimension = matrix_23.cast<double>()*v_3d;

//一些矩阵运算
//四则运算省去，直接用+-*/即可
matrix_33 = Matrix3d::Random();  //随机数矩阵
cout<<"random matrix: \n"<<matrix_33<<endl;
cout<<"tranpose: \n"<<matrix_33.transpose()<<endl;  //转置
cout<<"sum: \n"<<matrix_33.sum()<<endl;  //各元素之和
cout<<"trace: "<<matrix_33.trace()<<endl;   //迹
cout<<"times 10: \n"<<10*matrix_33<<endl;   //数乘
cout<<"inverse: \n"<<matrix.inverse()<<endl;  //逆
cout<<"det: "<<matrix_33.determinant()<<endl;  //行列式

//特征值
//实对称矩阵可以保证对角化成功
SelfAdjointEigenSolver<Matrix3d> eigen_solver(matrix_33.transpose()*matrix_33);
cout<<"Eigen values = \n"<<eigen_solver.eigenvalues()<<endl;
cout<<"Eigen vectors = \n"<<eigen_solver.eigenvectors()<<endl;

//解方程
//求解 matrix_NN*x = v_Nd;
//N的大小在前面的宏定义里面，它由随机数生成
//直接求逆自然是是最直接的，但是运算量大

Matrix<double,MATRIX_SIZE,MATRIX_SIZE> matrix_NN = MatrixXd::Random();
matrix_NN =matrix_NN*matrix_NN.transpose();
Matrix<double,MATRIX_SIZE,1> v_Nd = MatrixXd::Random(MATRIX_SIZE,1);

clock_t  time_stt = clock(); //计时
//直接求逆
Matrix<double,MATRIX_SIZE,1> X = matrix_NN.inverse()*v_Nd;

cout<<"time of normal inverse is "<<1000*(clock()-time_stt)/(double)CLOCKS_PER_SEC<<"ms"<<endl;
cout<<"x = :"<<x.transpose()<<endl;

//通常用矩阵分解来求解，例如QR分解，速度会快很多
time_stt =clock();
x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
cout<<"time of Qr decomposition is "<<1000*(clock()-time_stt)/(double)CLOCKS_PER_SEC<<"ms"<<endl;
cout<<"x = :"<<x.transpose()<<endl;

//对于正定矩阵，还可以用cholesky分解来解方程
time_stt =clock();
x = matrix_NN.ldlt().solve(v_Nd);
cout<<"time of ldlt decomposition is "<<1000*(clock()-time_stt)/(double)CLOCKS_PER_SEC<<"ms"<<endl;
cout<<"x = :"<<x.transpose()<<endl;
}

这个例程演示了Eigen的基本操作。要编译这个代码，需要在CMakeList.txt里指定Eigen的头文件目录

#指定头文件
include_directories("/usr/include/eigen3")

KDE可能不会提示C++的成员运算(比如inverse()),忽略即可。

上面的代码看懂没问题。常用的记住就行了，其他的用的时候再查。

3.3 旋转向量与欧拉角

3.3.1 旋转向量

旋转矩阵描述旋转的缺点

1. SO(3)的旋转矩阵由9个量，但一次旋转指由三个自由度。所以旋转矩阵有点冗余。同样变换矩阵16个量表达6个自由度。。。
2. 旋转矩阵自身带有约束：它必须是个正交矩阵，且行列式为1，变换矩阵同样一堆约束

所有，就有了一个很明显的需求：有没有一种方式可以紧凑的表达旋转和平移？

例如，用一个三维向量表达旋转，一个六维向量表达变换，是否可行？

当然可行，实际上任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是，我们可以用一个向量，其方向与旋转轴一致，长度等于旋转角。这种向量称为旋转向量(或轴角/角轴，Axis-Angle),只需要一个三维向量即可描述旋转。

同样，对于变换矩阵，我们选择使用一个旋转向量和一个平移向量即可表达一次变换。这时的变量维数刚好为6。

从选装向量到旋转矩阵的转换过程：罗德里格斯公式

没搞明白的地方：取两边的迹。哦想明白了n为单位向量，然后。。。n*nT对角线元素之和为1.

补充下 迹 的概念。

3.3.2 欧拉角

因为旋转向量和旋转矩阵不直观，所以，欧拉角应运而生。

发动空间想象理解一下万向锁。

3.4 四元数

四元数的推导和定义以及运算不想在这里深究，研究起来又是一本书。。。

3.4.3 用四元数表示旋转(重点)

3.4.4 四元数到其他旋转表示的旋转

任意单位四元数描述了一个旋转，注意是单位四元数。

直接拿结论吧：

3.6 实践：Eigen的几何模块

接下来我们将在Eigen使用四元数、欧拉角和旋转矩阵，演示他们之间的变换关系。

#include <iostream>
#include <cmath>
using namespace std;

#include <Eigen/Core>
#include <Eigen/Geometry>

using namespace Eigen;
//本程序演示了Eigen几何模块的使用方法

int main(int argc,char** argv)
{
//Eigen/Geometry模块提供了各种旋转和平移的表示
//3D旋转矩阵直接使用Matrix3d或Matrix3f
Matrix3d rotation_matrix = Matrix3d::Identity();
//旋转向量使用AngleAxis
AngleAxisd rotation_vector(M_PI/4,Vector3d(0,0,1));  //沿z轴旋转45°
cout.precision(3);
cout<<"rotation matrix =\n"<<rotation_vector.matrix()<<endl;  //用matrix()转化成矩阵，也可以直接赋值

rotation_matrix = rotation_vector.toRotationMatrix();

//用AngleAxis可以进行坐标变换
Vector3d v(1,0,0);
Vector3d v_rotated = rotation_vector*v;
cout<<"(1,0,0) after rotation (by angle axis) = "<<v_rotated.transpose()<<endl;

//使用旋转矩阵
v_rotated = rotation_matrix*v;
cout<<"(1,0,0) after rotation (by matrix) = "<<v_rotated.transpose()<<endl;

//欧拉角：可以将旋转矩阵直接 转换成欧拉角
Vector3d euler_angles = rotation_matrix.eulerAngles(2,1,0); //ZYX顺序
cout<<"ypr"<<euler_angles.transpose()<<endl;

//欧式变换矩阵使用Eigen::Isometry
Isometry3d T = Isometry3d::Identity(); //虽然称为3d，实质上是4*4的矩阵
T.rotate(rotation_vector);  //按照rotation_vector进行旋转 
T.pretranslate(Vector3d(1,3,4));   //把平移向量设置为(1,3,4)
cout<<"Transform matrix = \n"<<T.matrix()<<endl;

//用变换矩阵进行坐标变换
Vector3d v_transformed = T*v;   //相当于R*v+t
cout<<"v transformed = "<<v_ttransformed.transpose()<<endl;

//对于仿射变换和射影变换，使用Eigen::Affine3d和Eigen::Projective3d即可

//四元数
//可以直接把AngleAxis赋值给四元数，反之亦然
Quaternioned q = Quaterninoed(rotation_vector);
cout<<"quaternion form rotation vector = "<<q.coeffs().transpose()<<endl;
//请注意coeffs的顺序是(x,y,z,w),w为实部，前三者为虚部
//也可以把旋转矩阵赋给它
q = Quaterniond(rotation_matrix);
cout<<"quaternion from rotation matrix = "<<q.coeffs().transpose()<<endl;
//使用四元数旋转一个向量，使用重载的乘法即可
v_rotated = q*v;   //注意数学上
cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;
//用常规向量乘法表示，则计算如下
cout<<"should be equal to "<<(q*Quaterniond(0,1,0,0)*q.inverse()).coeffs().transpose()<<endl;

return 0;
}

Eigen中对各种形式的表达如下。请注意每种类型都有单精度和双精度两种数据类型，而且和之前一样，不能由编译器自动转换。

• 旋转矩阵(3x3):Eigen::Matrix3d
• 旋转向量(3x1):Eigen::AngleAxisd
• 欧拉角(3x1):Eigen::Vector3d
• 四元数(4x1):Eigen::Quaterniond
• 欧式变换矩阵:Eigen::Isomotery3d

注意：

实例演练：

#include <iostream>
#include <Eigen/Core>
#include <Eigen/Geometry>

int main()
{
Eigen::Quaterniond q1(0.35,0.2,0.3,0.1),q2(-0.5,0.4,-0.1,0.2);
q1.normalize();
q2.normalize();
Eigen::Vector3d t1(0.3,0.1,0.1),t2(-0.1,0.5,0.3),p1(0.5,0,0.2);

Eigen::Isomotery3d T1w(q1),t2w(q2);
T1w.pretranslate(t1);
T2w.pretranslate(t2);

Eigen::Vector3d p2 = T2w*T1w.inverse()*p1;
std::cout<<std::endl<<p2.transpose()<<endl;
return 0;
}

3.7 可视化演示

3.7.1 显示运动轨迹

我们通过某种方式记录了一个机器人的运动轨迹，现在想把它画到一个窗口中。假设文件存储于trajectory.txt,每一行用下面的格式存储：

time,tx,ty,tz,qx,qy,qz,qw,

其中time指该位姿记录的时间，t为平移，q为旋转四元数，均是以世界坐标系到机器人坐标系记录。下面我们从文件中读取这些轨迹，并显示到一个窗口。

在画轨迹的时候我们可以把“轨迹”画成一系列点组成的序列，这会和我们想象中的轨迹比较相似。严格来说，这其实是机器人(相机)坐标系的原点在世界坐标系中的坐标。考虑机器人坐标系的原点，即OR，那么，此时OW就是这个原点在世界坐标系下的坐标：

OW = TWR*OR=tWR

这正是TWR的平移部分。因此从TWR中直接看到相机在何处，这也是我们说TWR更为直观的原因。因此，在可视化程序里，轨迹文件存储了，TWR而不是TRW。

且看下面的程序：

#include <pangolin/pangolin.h>
#include <Eigen/Core>
#include <unistd.h>

using namespace std;
using namespace Eigen;

//path to trajectory file
string trajectory_file = "自己的路径，自己填写合适的参数"；

void DrawTrajectory(vector<Isometory3d,Eigen::aligned_allocator<Isometry>>);

int main(int argc,int char**)
{
vector<Ismotery,Eigen::aligned_allocator<Isometry>> poses;
ifstream fin(trajectory_file );
if(!fin)
{
cout<<"cannot find trajectory file at "<<trajectory_file<<endl;
return 1;
}

while(!fin.eof())
{
double time,tx,ty,tz,qx,qy,qz,qw;
fin>>time>>tx>>ty>>tz>>qx>>qy>>qz>>qw;
Isometry3d Twr(Quaterniond(qw,qx,qy,qz));
Twr.pretranslate(Vector3d(tx,ty,tz));
poses.push_back(Twr);
}
cout<<""<<poses.size()<<" pose entires"<<endl;

//draw trajectory in pangolin
DrawTrajectory(poses);
return 0;
}

void DrawTrajectory(vector<Isometry3d, Eigen::aligned_allocator<Isometry3d>> poses) {
  // create pangolin window and plot the trajectory
  pangolin::CreateWindowAndBind("Trajectory Viewer", 1024, 768);
  glEnable(GL_DEPTH_TEST);
  glEnable(GL_BLEND);
  glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

  pangolin::OpenGlRenderState s_cam(
    pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
    pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
  );

  pangolin::View &d_cam = pangolin::CreateDisplay()
    .SetBounds(0.0, 1.0, 0.0, 1.0, -1024.0f / 768.0f)
    .SetHandler(new pangolin::Handler3D(s_cam));

  while (pangolin::ShouldQuit() == false) {
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
    d_cam.Activate(s_cam);
    glClearColor(1.0f, 1.0f, 1.0f, 1.0f);
    glLineWidth(2);
    for (size_t i = 0; i < poses.size(); i++) {
      // 画每个位姿的三个坐标轴
      Vector3d Ow = poses[i].translation();
      Vector3d Xw = poses[i] * (5 * Vector3d(1, 0, 0));
      Vector3d Yw = poses[i] * (5 * Vector3d(0, 1, 0));
      Vector3d Zw = poses[i] * (5 * Vector3d(0, 0, 1));
      glBegin(GL_LINES);
      glColor3f(1.0, 0.0, 0.0);
      glVertex3d(Ow[0], Ow[1], Ow[2]);
      glVertex3d(Xw[0], Xw[1], Xw[2]);
      glColor3f(0.0, 1.0, 0.0);
      glVertex3d(Ow[0], Ow[1], Ow[2]);
      glVertex3d(Yw[0], Yw[1], Yw[2]);
      glColor3f(0.0, 0.0, 1.0);
      glVertex3d(Ow[0], Ow[1], Ow[2]);
      glVertex3d(Zw[0], Zw[1], Zw[2]);
      glEnd();
    }
    // 画出连线
    for (size_t i = 0; i < poses.size(); i++) {
      glColor3f(0.0, 0.0, 0.0);
      glBegin(GL_LINES);
      auto p1 = poses[i], p2 = poses[i + 1];
      glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
      glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
      glEnd();
    }
    pangolin::FinishFrame();
    usleep(5000);   // sleep 5 ms
  }
}

课后题：

先标个链接：https://blog.csdn.net/qq_17032807/article/details/84928910

1. 验证旋转矩阵是正交矩阵。

思路：主要证明R的转置和R的逆相等就行了。

同时要明白正交矩阵的定义。

2.寻找罗德里格斯公式的推导并理解

其中k为旋转轴。

根据图中的几何关系可得：

且垂直分量和平行分量各自的旋转分量为：

带入：

上述表达为矢量运算的表达式，对于矩阵运算，形式需要改变一下。首先就在线性变换中，可以采取一种反对称矩阵进行矩阵变换，其中为：

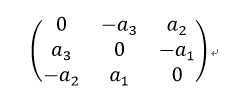
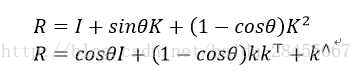
3.验证式3.33

四元数的运算法则。

4.旋转矩阵、旋转向量、欧拉角、四元数的关系。

5.  

6.一般线性方程有多少个解？

一般分为直接法和雅克比迭代法。直接法分为：1.直接求逆法，运算量大，仅对方阵有效，很可能没解；2.QR分解法，一般比较常用，方程就算方程无解也会得到近似解；3.最小二乘求解，和QR类似；4.LU分解法，仅仅对于方阵有效；5.cholesky分解法，也仅仅适合方阵。雅克比迭代法属于一种数值求解法，需要计算方程的雅克比矩阵以及设计迭代策略。