本文探讨了在微变等效电路分析中，双口网络的混合参数模型。重点在于理解小信号下的△ib与△ube关系，以及它们与其他△量之间的联系。通过全微分，建立了电压和电流的等效关系，并解释了h参数的含义，如h11对应rbe，h21相当于β，而h22与rce相关。同时，讨论了忽略某些电阻后的简化模型，强调在低频小信号条件下的有效性。此外，还提到了rbb、re和rb'e作为PN结电阻的等效概念。
上面的电流源依次是：直流交流都存在的瞬时值，直流，正弦交流量的向量，交流，交流有效值
现在讨论的是在△的条件下，△ib与△ube的关系及其他△量之间的关系
由上图可以看出来，在△的那个范围里，ube和ib近似于是线性的，就可以用rbe等效，Q点不同，rbe就不同，静态影响在这里体现出来
上面是一个双口网络，可以做混合参数模型（电路知识）
ube与ib和uce有关，为什么和uce有关呢？参照下面的三个图
已经有了上面的关系，现在想求的是每个△之间的关系，那么就做全微分
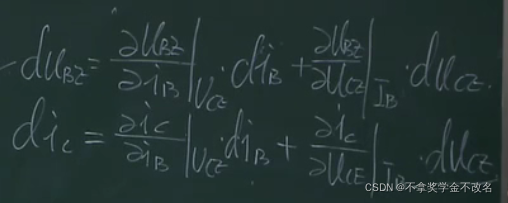
将微分量变成△量，然后进而改写
根据上面的式子，电压等于后面两个相加的话，那就是电压串联
电流相加的话就是两个电流并联，则得到了下面的等效电路图（条件是输入是低频小信号）
为什么是混合参数？因为里面的h都是不同的量纲（电路知识）
到底里面的h参数的含义是什么？
h11就是我们前面说的rbe，h12说是对uce的波动（没太懂），因为大于1v的时候不怎么变化了，所以就非常小，这个参数几乎可以忽略，上节课推导没考虑这个影响
h21实际上就是beta，h22表示的就是上面的b图那一族曲线的某一条线的上翘，大小与平缓相关
，也就是rce的等效电阻分之一，这个电阻非常大，大概百k，负载电阻没有达到可以和他媲美的时候，基本上就是算作断路，所以电阻分之一也基本上是很小的值，也可以忽略，所以就有了简化的h参数，也就是上节课的微变等效电路（撒花）
上图就是rbe的等效电路图
rbb撇就是基区的体电阻，这个电阻可以在手册上得到
re撇发射极的体电阻，因为掺杂了较高的浓度，所以电阻值比较小
rb撇e撇实际上就是pn结电阻，Ut/id（之前讲的），这里的id实际就是ie，实际上就是和ieq相关（也没太懂）
根据上面的那个电路推出来的，把小电阻忽略了
rb撇e撇就是pn结的动态等效电阻
上面这个应该就是之前推出来的那个式子，ut就是与温度相关的常数好像
这块ieq等于（1+beta）ieq，那么分子分母就会约分了，就可以写成下面的式子，为什么不写成这样呢？因为下面这么写没有物理意义，虽然式子是对的
扫一扫
2168
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
