机械臂机器人——使用Matlab Robotic ToolBox建立四轴机械臂模型并实现运动控制仿真

最新推荐文章于 2025-03-20 11:34:08 发布

Irving.Gao

最新推荐文章于 2025-03-20 11:34:08 发布

阅读量2.2w

点赞数 47

分类专栏：智能机器人开发 Matlab 文章标签： matlab

本文链接：https://blog.csdn.net/qq_45779334/article/details/115249922

版权

智能机器人开发同时被 2 个专栏收录

9 篇文章

订阅专栏

Matlab

5 篇文章

订阅专栏

文章目录

为了能够实现机械臂的运动轨迹规划，同时更加深入学习机器人学相关理论知识，并将其运用在时间当中，我采用Robotic ToolBox建立四轴机器人模型并实现运动控制仿真，并作以记录分享。

四轴机械臂实物

在这里插入图片描述

Robotic ToolBox机械臂建模

1.建立机械臂的D-H表

在这里我选用的是标准D-H参数进行建模，各个参数含义如图所示：
在这里插入图片描述
需要注意的是：

在确定轴线时，Z轴为连杆关节的旋转轴（在这里即舵机的旋转轴），X轴为当前关节的Z轴和下一关节（一个一个往上走）的Z轴的公垂线（在这里就是机械臂杆的平行线）。

建立机械臂坐标系

坐标系建立方法：
在这里插入图片描述
该机械臂坐标系建立如图所示：

根据坐标系建立D-H表

首先需要做的就是给该机械臂建立D-H表：

i	a(单位:m)	alpha
1	0	pi/2(z1绕x1旋转90°到z2)
2	0.105	0
3	0.09	0
4	0.04	0

2.代码建模

%% 机械臂建模
% 定义各个连杆以及关节类型，默认为转动关节
%           theta      d        a        alpha
L1=Link([       0       0      0     pi/2 ], 'standard'); % [四个DH参数], options
L2=Link([    0         0       0.105       0], 'standard');
L3=Link([     0           0  0.09      0], 'standard');
L4=Link([     0        0   0.04     0], 'standard');

robot=SerialLink([L1,L2,L3,L4]); % 将四个连杆组成机械臂
robot.name='4DOF Robotic Arm';
robot.display();
view(3); % 解决robot.teach()和plot的索引超出报错
robot.teach();
robot.plot([0 pi/2 0 0]);

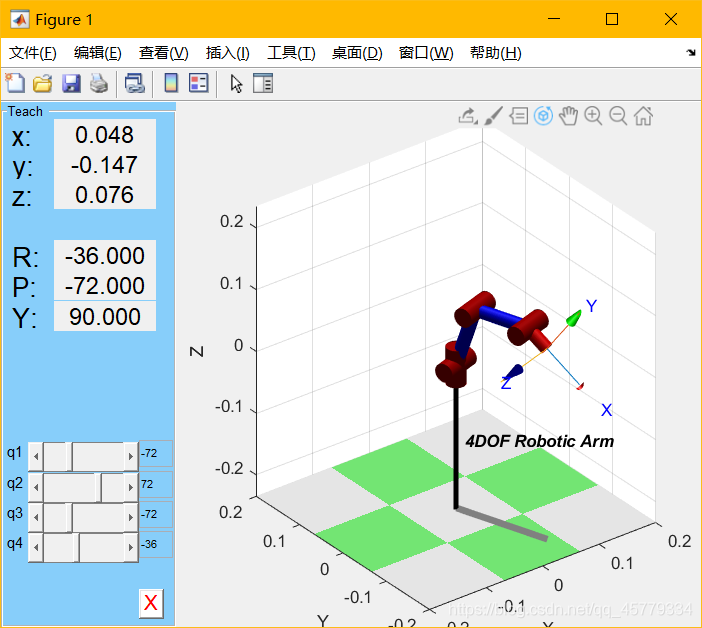
在这里插入图片描述

机械臂运动学仿真

1.正运动学仿真

给定每个关节的转动角度，让机器人实现运动控制。

clc;
clear;
%% 机械臂建模
% 定义各个连杆以及关节类型，默认为转动关节
%          theta      d       a      alpha
L1=Link([     0       0        0      pi/2], 'standard'); % [四个DH参数], options
L2=Link([     0       0      0.105     0], 'standard');
L3=Link([     0       0      0.09      0], 'standard');
L4=Link([     0       0      0.04      0], 'standard');
b=isrevolute(L1);
robot=SerialLink([L1,L2,L3,L4],'name','Irvingao Arm'); % 将四个连杆组成机械臂
robot.name='4DOF Robotic Arm';
robot.display();

%% 轨迹规划
% 初始值及目标值
init_ang=[0 0 0 0];
targ_ang=[0, -pi/6, -pi/5, pi/6];
step=200;

[q,qd,qdd]=jtraj(init_ang,targ_ang,step); %关节空间规划轨迹，得到机器人末端运动的[位置，速度，加速度]
T0=robot.fkine(init_ang); % 正运动学解算
Tf=robot.fkine(targ_ang);
subplot(2,4,3); i=1:4; plot(q(:,i)); title("位置"); grid on;
subplot(2,4,4); i=1:4; plot(qd(:,i)); title("速度"); grid on;
subplot(2,4,7); i=1:4; plot(qdd(:,i)); title("加速度"); grid on;

Tc=ctraj(T0,Tf,step); % 笛卡尔空间规划轨迹，得到机器人末端运动的变换矩阵
Tjtraj=transl(Tc);
subplot(2,4,8); plot2(Tjtraj, 'r');
title('p1到p2直线轨迹'); grid on;
subplot(2,4,[1,2,5,6]);
plot3(Tjtraj(:,1),Tjtraj(:,2),Tjtraj(:,3),"b"); grid on;
hold on;
view(3); % 解决robot.teach()和plot的索引超出报错
qq=robot.ikine(Tc, 'q0',[0 0 0 0], 'mask',[1 1 1 1 0 0]); % 逆解算
robot.plot(qq);

机械臂运动效果如下：

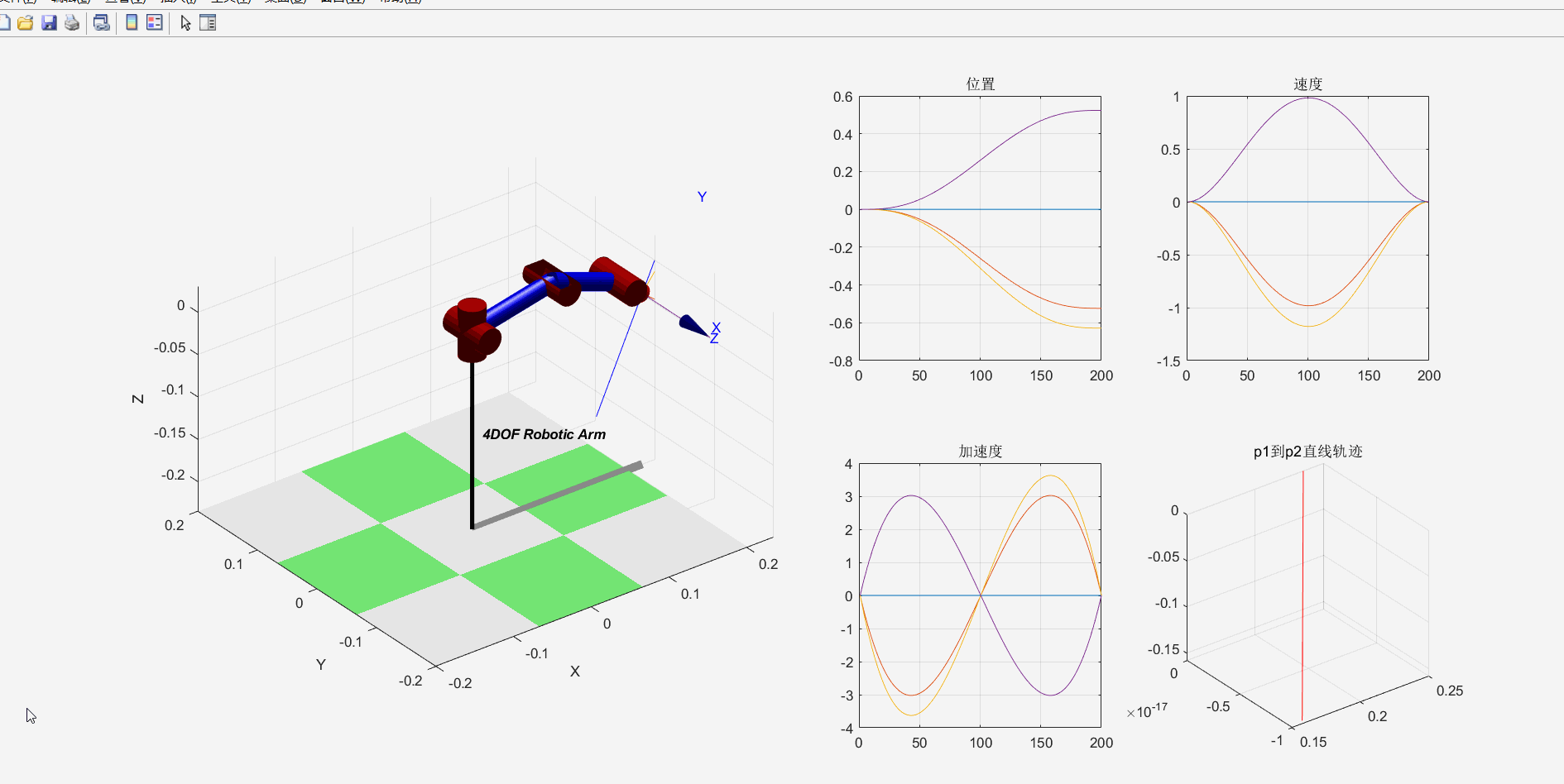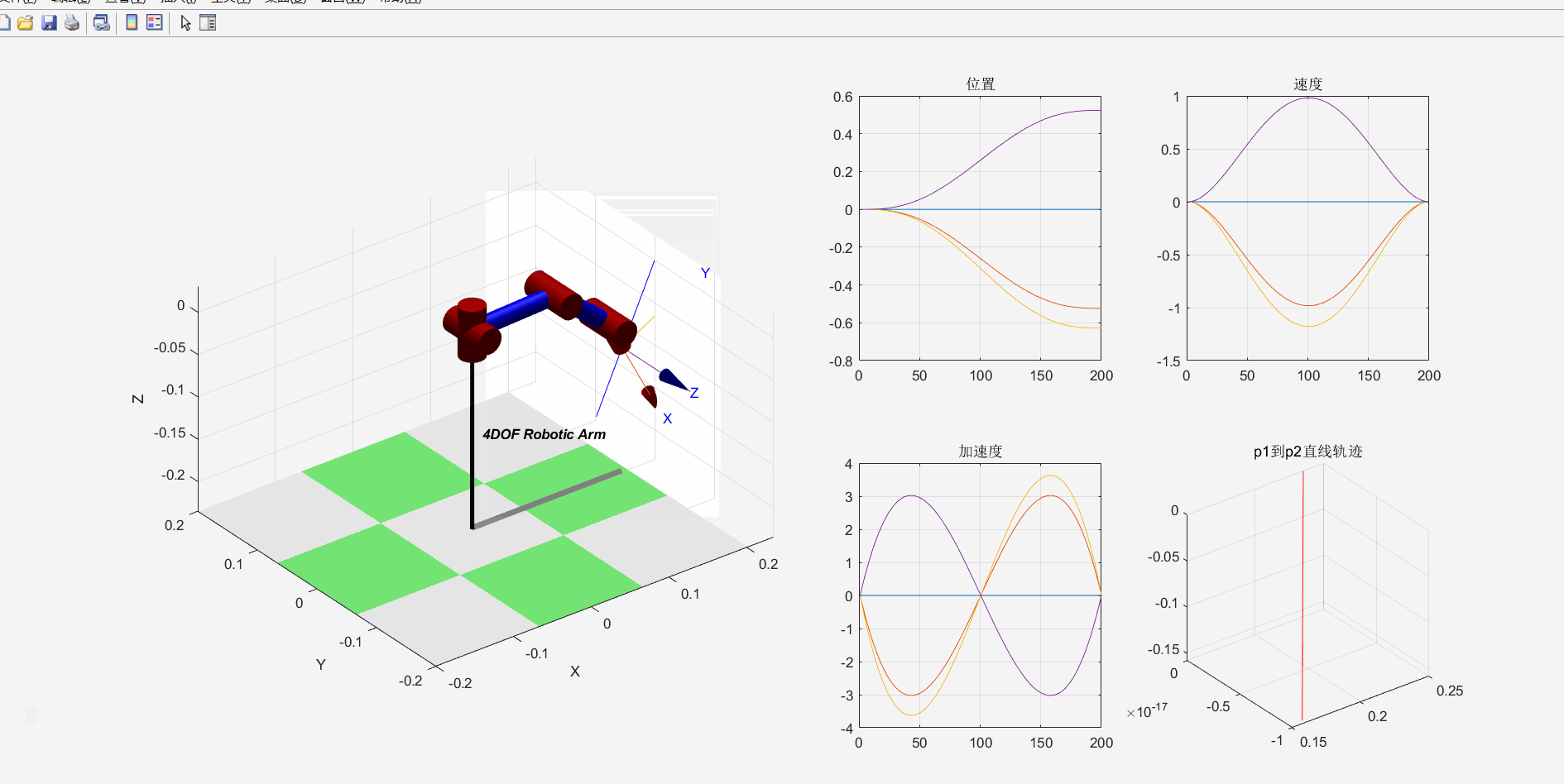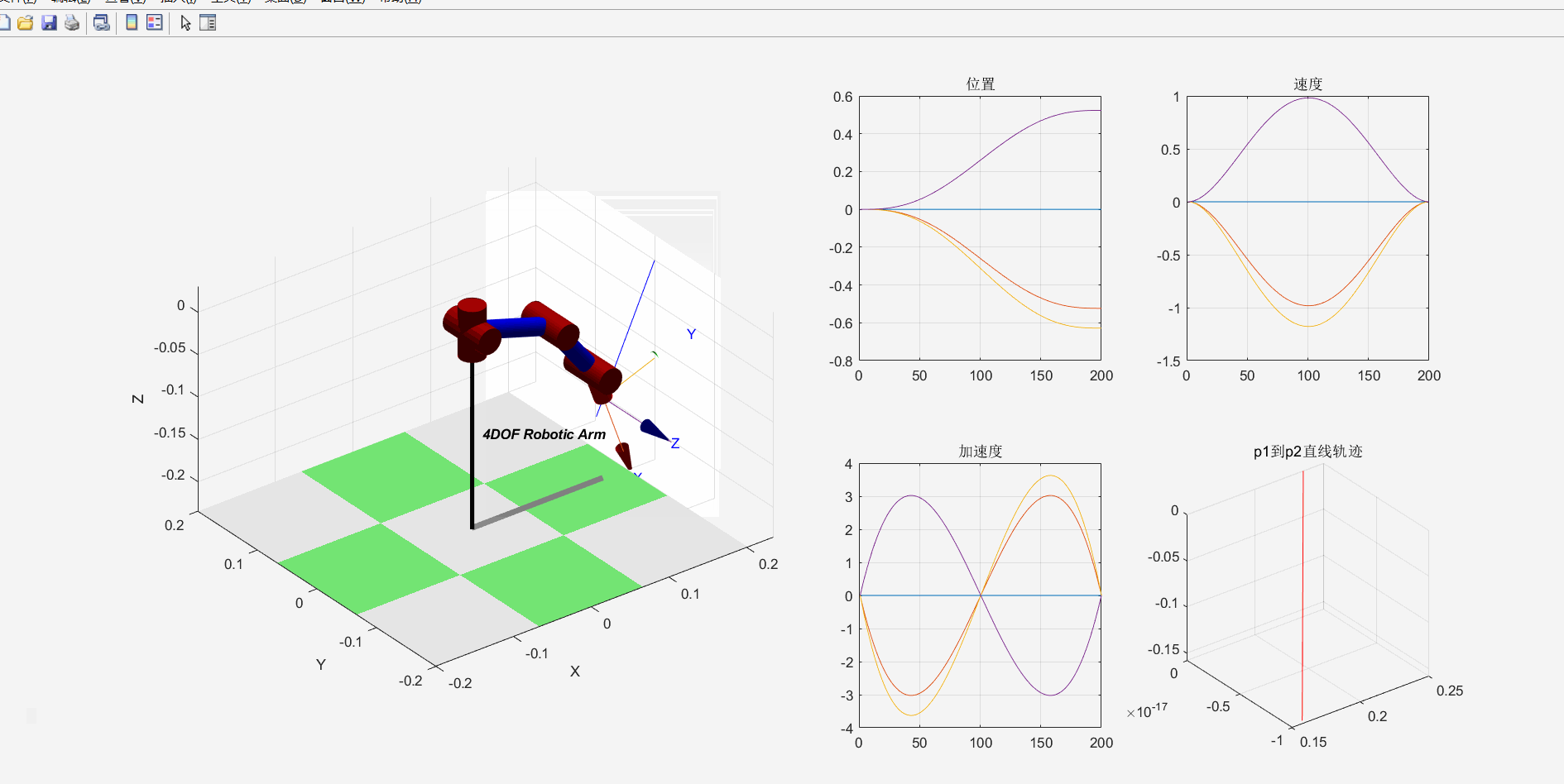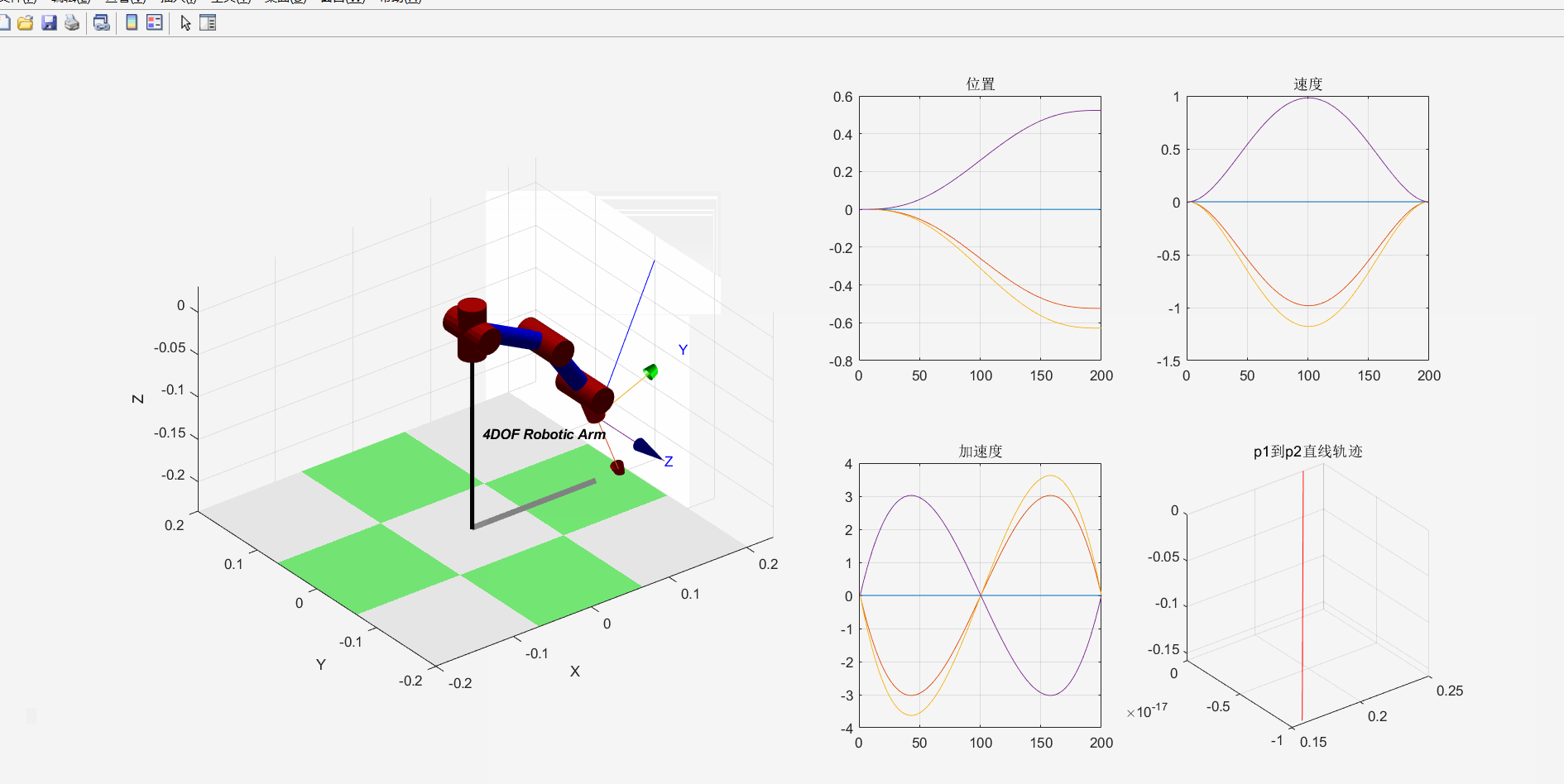
在这里插入图片描述

2.逆运动学仿真

在这里为了我们方便定义目标点的坐标，所以我们将a的单位改成m。

%% 机械臂建模
% 定义各个连杆以及关节类型，默认为转动关节
%          theta      d       a      alpha
L1=Link([     0       0        0      pi/2], 'standard'); % [四个DH参数], options
L2=Link([     0       0      10.5     0], 'standard');
L3=Link([     0       0      9      0], 'standard');
L4=Link([     0       0      4      0], 'standard');

b=isrevolute(L1);
robot=SerialLink([L1,L2,L3,L4],'name','Irvingao Arm'); % 将四个连杆组成机械臂
robot.name='4DOF Robotic Arm';
robot.display();
view(3);
robot.teach();
robot.plot([0 pi/2 0 0]);

参考文章：