【机器人工具箱学习笔记】第三章 时间与运动

函数记录

tpoly() %生成一个五次多项式轨迹
lspb() %生成抛物线过渡轨迹
mean() %求平均值
max() %求最大值
mtraj() %多维轨迹
mstraj() %有中间点的轨迹连接轨迹
numrows() %行数
interp() %沿路径单位化距离s∈[0,1]中的位姿插值//%两个位姿之间50个分布的轨迹
ctraj() %时间平滑轨迹
p() %位姿插值
skew() %角速度斜对称矩阵
vex() %将斜对称矩阵转换成一个向量
tr2delta() %求小变换位姿的平移增量和旋转增量
trnorm() %施密特正交化后规范化
q.dot() %四元数规范化
q.unit() %四元数规范化

学习记录

轨迹

• poly：五次多项式

• lspb：直线与抛物线混合轨迹

• mtraj：将平滑的标量轨迹扩展成向量

• mstraj：基于中间点矩阵生成一个多段多轴轨迹

• interp：生成插值

• ctraj：轨迹插值

平滑一维轨迹

>> tpoly(0, 1, 50); %生成一个五次多项式轨迹
>> [s,sd,sdd] = tpoly(0, 1, 50); %相应的速度加速度
>> tpoly(0, 1, 50, 0.5, 0); %设置初始速度和终点速度
>> mean(sd) / max(sd) %求平均值,结果只有最大值的52%
ans =
    0.5231
>> lspb(0, 1, 50); %生成抛物线过渡轨迹
>> [s,sd,sdd] = lspb(0, 1, 50); %生成指定速度的抛物线过渡轨迹
>> max(sd) %函数lspb自己选择的直线段速度
>> s = lspb(0, 1, 50, 0.025);
>> s = lspb(0, 1, 50, 0.035);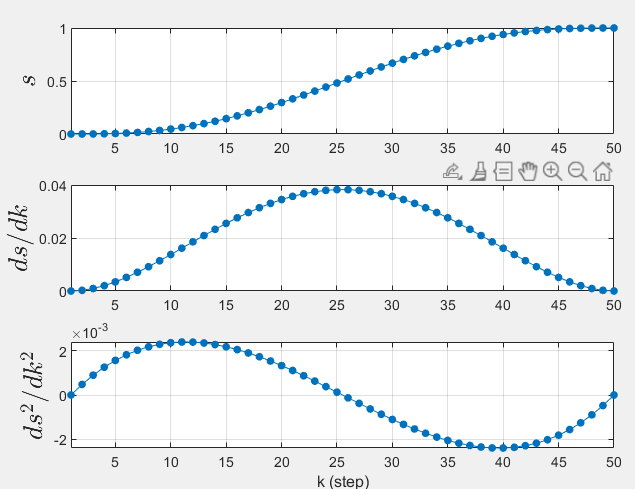

起点和终点速度均为0的五次多项式轨迹

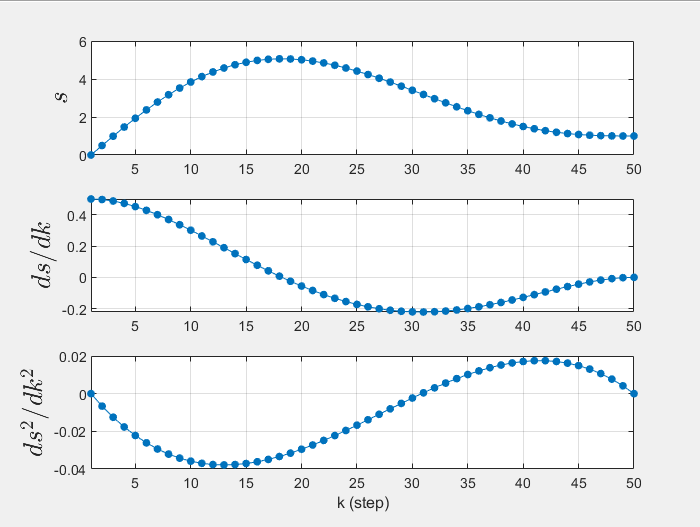
起点速度为0.5，终点速度为0的五次多项式轨迹

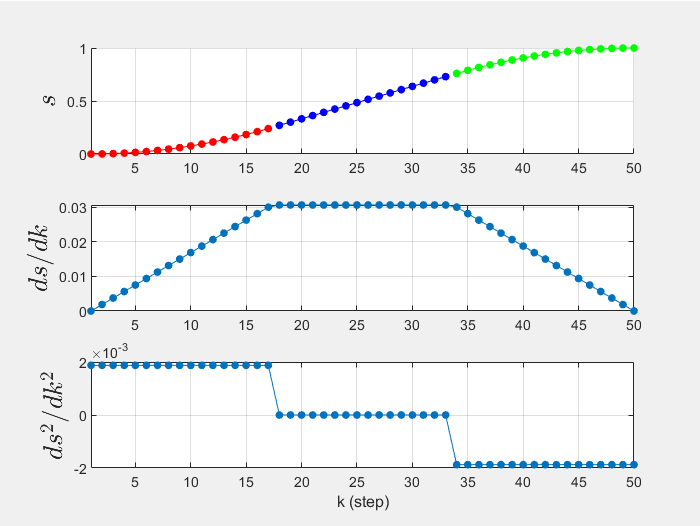
直线与抛物线混合轨迹

多维轨迹

>> q = mtraj(@lspb, [0 2], [1 -1], 50); %多维轨迹
>> plot(q) 
>> q = [T1.t' T1.torpy] %将位姿齐次矩阵转换为一个六维向量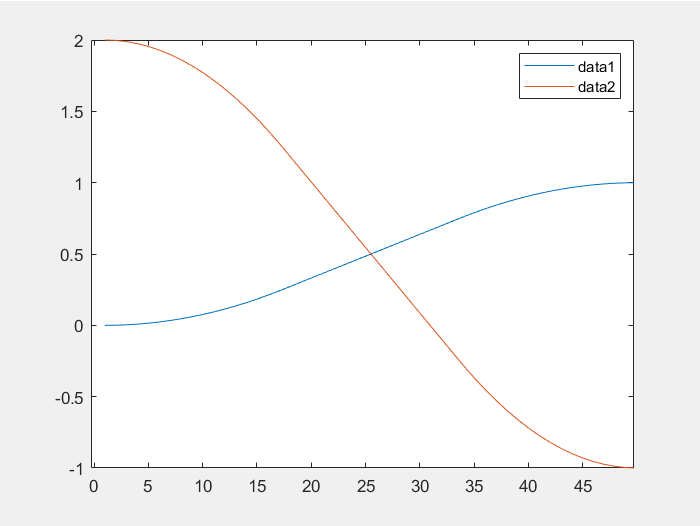

多维运动，x1从0到1变化，x2从2到-1变化

多段轨迹

>> via = SO2(30, 'deg') * [-1 1; 1 1; 1 -1; -1 -1]'; %经过的轨迹
%基于中间点矩阵生成一个多段多轴轨迹，参数是：
%中间点矩阵，每轴的最大速度向量，每段的运动时间向量，起点各轴坐标，采样时间间隔，加速时间
>> q0 = mstraj(via(:,[2 3 4 1])', [2,1], [], via(:,1)', 0.2, 0); %[2 3 4 1]表示从第2列运动到3,4,1列，第一列是起点
>> plot(q0(:,1), q0(:,2))
>> q2 = mstraj(via(:,[2 3 4 1])', [2,1], [], via(:,1)', 0.2, 2); %增加加速时间，轨迹会更加圆滑
>> hold on
>> plot(q2(:,1), q2(:,2))
>> [numrows(q0) numrows(q2)] %更光滑的轨迹也会花更多的时间
ans =
    28    80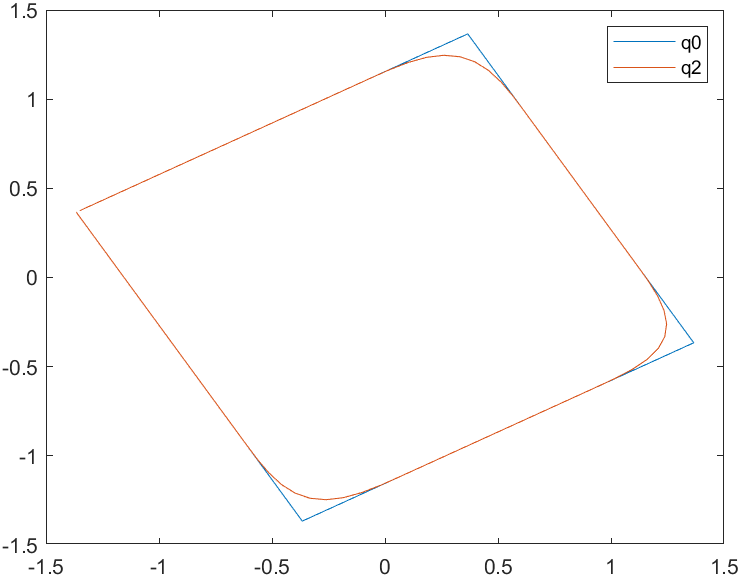

三维空间姿态插值

%定义两个姿态
>> R0 = SO3.Rz(-1) * SO3.Ry(-1);
>> R1 = SO3.Rz(1) * SO3.Ry(1);
%得到等价横滚-俯仰-偏航角
>> rpy0 = R0.torpy();
>> rpy1 = R1.torpy();
>> rpy = mtraj(@tpoly, rpy0, rpy1, 50);  %分50个时间布在它们之间生成一条轨迹
>> SO3.rpy( rpy ).animate; %通过动画展示轨迹变化过程
>> q0 = R0. UnitQuaternion; q1 = R1.UnitQuaternion; %找到与两个位姿等价的四元数
>> q = interp(q0, q1, 50); %对它们进行插值
>> about(q)
q [UnitQuaternion] : 1x50 (1.6 kB)
>> q.animate

旋转方向

>> q0 = UnitQuaternion.Rz(-2); q1 = UnitQuaternion.Rz(2);
>> q = interp(q0, q1, 50); %围绕z轴旋转，从−2弧度到+2弧度
>> q.animate()
>> q = interp(q0, q1, 50, 'shortest'); %旋转插值选择最短路径
>> q.animate()

笛卡尔运动

>> T0 = SE3([0.4, 0.2, 0]) * SE3.rpy(0, 0, 3);
>> T1 = SE3([-0.4, -0.2, 0.3]) * SE3.rpy(-pi/4, pi/4, -pi/2);
>> interp(T0, T1, 0.5) %沿路径单位化距离s∈[0,1]中的位姿插值
>> Ts = interp(T0, T1, 50); %两个位姿之间50个分布的轨迹
>> Ts. animate  %动画
>> P = Ts.transl; %轨迹的平动部分
>> about(P)
P [double] : 50x3 (1.2 kB) %以矩阵形式返回轨迹的笛卡尔位置
>> plot(P);
>> rpy = Ts.torpy; %轨迹的转动部分
>> plot(rpy);
>> Ts = T0. interp(T1, lspb(0, 1, 50) ); %创建一个时间上平滑的轨迹
>> Ts = ctraj(T0, T1, 50); %创建一个时间上平滑的轨迹
>> P = Ts.transl;
>> plot(P);
>> rpy = Ts.torpy;
>> plot(rpy);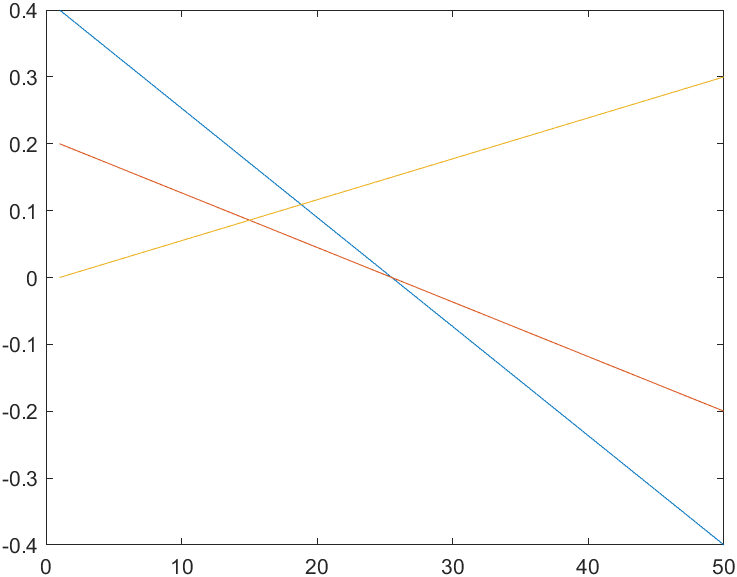

笛卡尔位置时间曲线

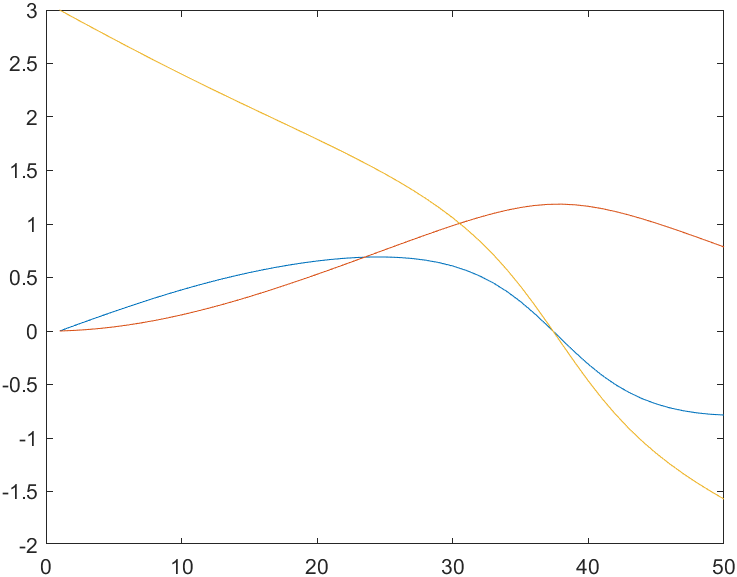
笛卡尔运动的RPY时间曲线

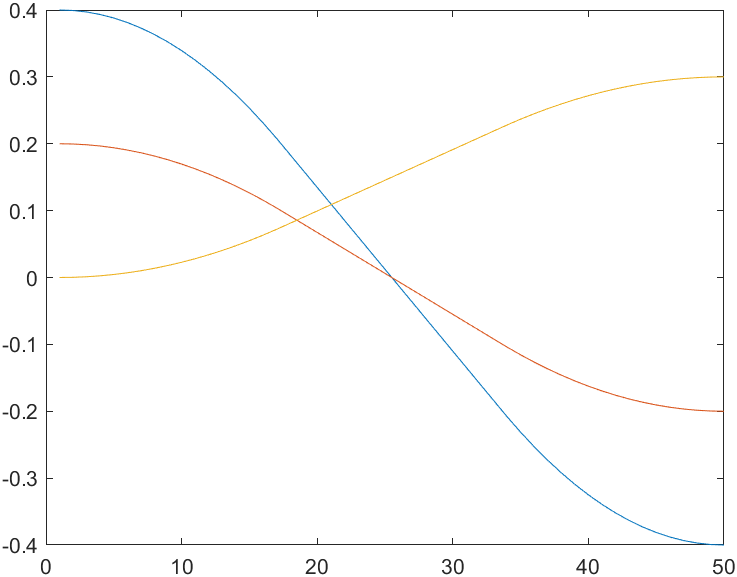
LSPB的笛卡尔位置时间曲线

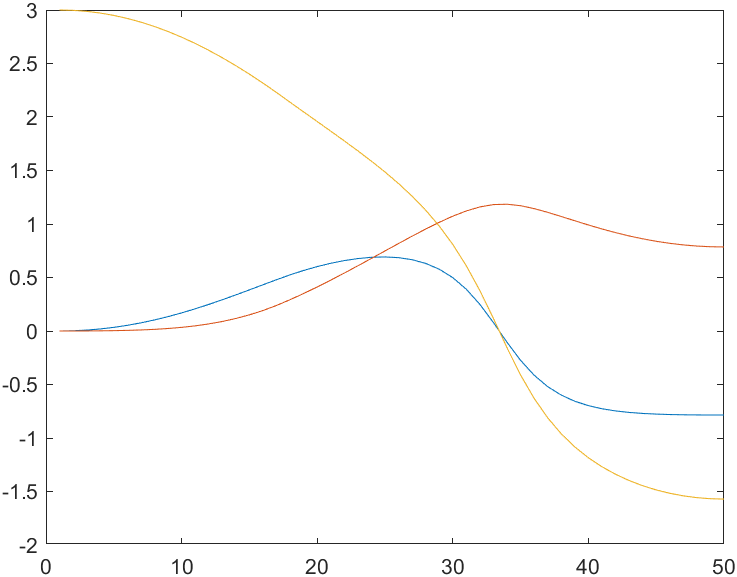
LSPB的RPY时间曲线

时变坐标系

%角速度斜对称矩阵
>> S = skew([1 2 3])
%将斜对称矩阵转换成一个向量
>> vex(S)'
%求小变换位姿的平移增量和旋转增量
>> d = tr2delta(T0,T1);
%求回去
>> delta2tr(d)*T0
%施密特正交化后规范化
>> T1=trnorm(T1);
%四元数规范化
>> qd = q.dot(omega);
>> q = q.unit();