【桁架优化】基于粒子群算法进行桁架优化附matlab代码

天天Matlab科研工作室

已于 2025-02-17 12:54:36 修改

阅读量1k

点赞数 20

分类专栏：优化求解文章标签：算法 matlab cocos2d

于 2023-12-10 21:34:54 首次发布

本文链接：https://blog.csdn.net/qq_59747472/article/details/134914989

版权

优化求解专栏收录该内容

844 篇文章

订阅专栏

✅作者简介：热爱科研的Matlab仿真开发者，擅长数据处理、建模仿真、程序设计、完整代码获取、论文复现及科研仿真。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知,完整Matlab代码及仿真咨询内容私信。

🌿 往期回顾可以关注主页，点击搜索

🔥 内容介绍

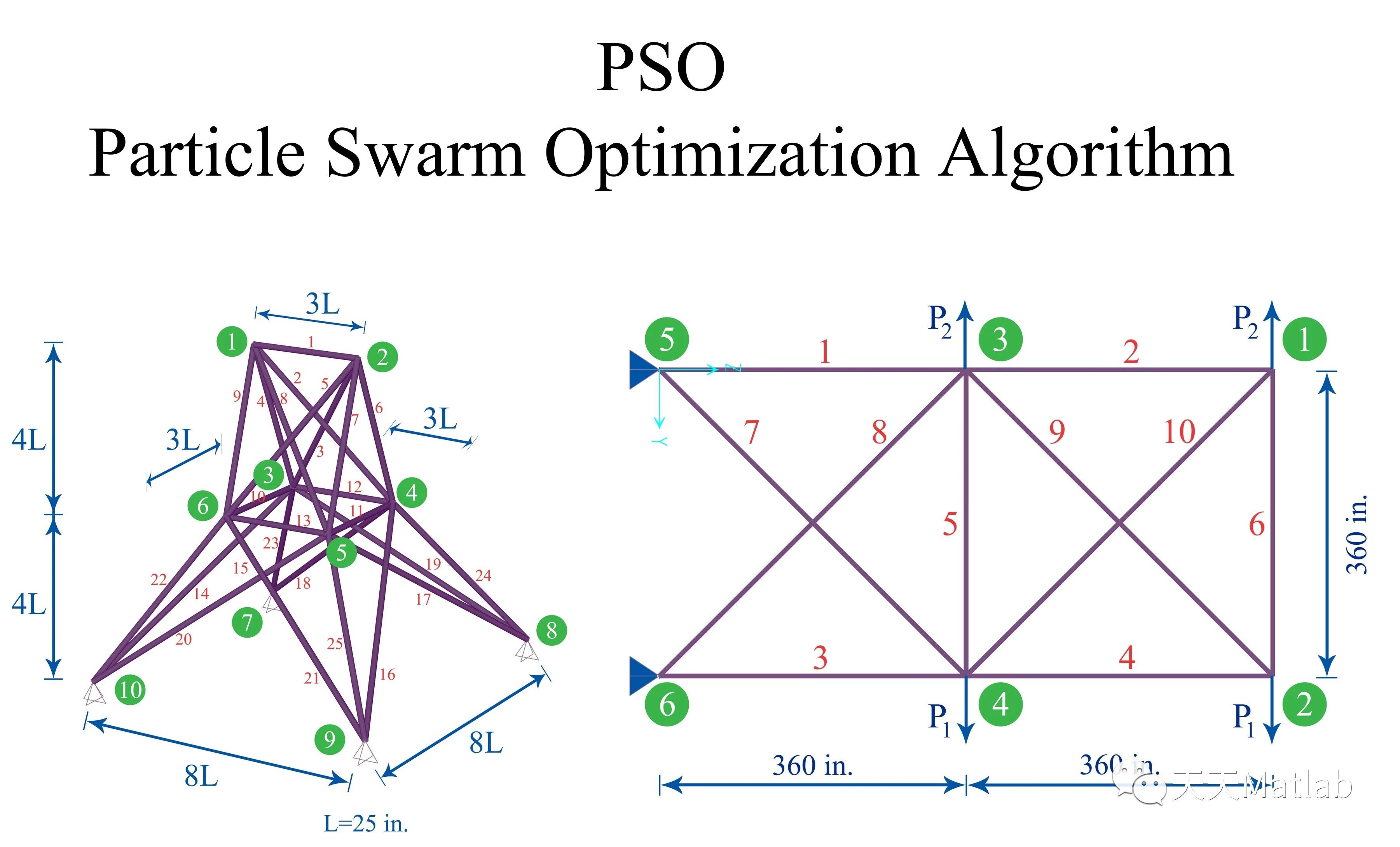
桁架结构是一种常见的工程结构，其设计和优化对于提高结构的稳定性和承载能力具有重要意义。在工程实践中，通过优化桁架结构的设计参数，可以使得结构在保证强度和刚度的前提下，减少材料消耗，降低成本，提高结构的整体性能。粒子群算法作为一种优化算法，具有全局寻优能力和较好的收敛性，因此在桁架优化中得到了广泛的应用。

粒子群算法是一种模拟鸟群觅食行为的优化算法，通过模拟鸟群中个体之间的信息交流和协作，来寻找最优解。在桁架优化中，可以将每个设计参数看作是一个粒子，通过不断迭代更新粒子的位置和速度，最终找到最优的设计参数组合，从而得到最优的桁架结构。

在进行桁架优化时，首先需要确定设计参数的范围和约束条件，然后通过粒子群算法来搜索最优解。在算法的迭代过程中，粒子根据自身的位置和速度不断更新，同时根据历史最优解和全局最优解来调整搜索方向，最终收敛到最优解。通过粒子群算法，可以有效地优化桁架结构的设计参数，使得结构在保证强度和刚度的前提下，达到最佳的性能指标。

除了确定设计参数和优化算法外，桁架优化还需要考虑结构的稳定性和可行性。在进行桁架优化时，需要考虑结构的受力情况、材料的可行性和制造工艺等因素，以确保优化后的桁架结构能够满足实际工程需求。因此，在进行桁架优化时，需要综合考虑各种因素，以得到最优的设计方案。

总之，基于粒子群算法进行桁架优化是一种有效的方法，可以通过优化设计参数来提高桁架结构的整体性能。在工程实践中，通过粒子群算法的应用，可以使得桁架结构在保证强度和刚度的前提下，达到最佳的性能指标，从而满足实际工程需求。因此，粒子群算法在桁架优化中具有重要的应用前景，值得进一步研究和探讨。

📣 部分代码

function W = truss2ex10weight(Swarm)global number;number=number+1;[SwarmSize, Dim] = size(Swarm);% inputsn=6; m=10; LL=914.4; E=6894.757; P=445.5; sigU=17.225; sigL=-17.225; unit=0.00272;joint=[2*LL,LL;2*LL,0;LL,LL;LL,0;0,LL;0,0];assembly=[5,3;3,1;6,4;4,2;4,3;2,1;6,3;5,4;4,1;3,2];forceJ=[-1,0,0;-1,0,-P;-1,0,0;-1,0,-P;2,1,1;2,1,1];index = 2;W=zeros(1,SwarmSize);% end of inputsfor q=1:SwarmSize;    X=Swarm(q,:);    stretch= E.*X;    [Jforce,Mforce,Jdispl,Mdispl,stress,Weight] = ...    truss2(n,m,joint,assembly,forceJ,stretch,index,X,E,unit);    Mforce; stress;Weight;Jdispl;    SUU=((abs(stress)/sigU)-1);    t=1;h=2*n;    for s=1:2:h;        D(s)=Jdispl(t,2);        D(s+1)=Jdispl(t,3);        t=t+1;    end    DUU=((abs(D)/5.08)-1);        %Dynamically modified penaity value (NI=is the algorithm,s current    %iteration number)        %r=10;    %r=10*(1+0.2*(number-1));      r=number*(number^0.5);   %Determine the power of the penalty function    for qq=1:m        if SUU(qq)<1           z(qq)=1;        else           z(qq)=2;        end    %Determine the multy-stage assignment function        if SUU(qq)<=0           h(qq)=0;        elseif SUU(qq)<0.001           h(qq)=10;        elseif SUU(qq)<0.1           h(qq)=20;        elseif SUU(qq)<1           h(qq)=100;        else           h(qq)=300;        end          C(qq)=r*(h(qq)*max(0,SUU(qq)^z(qq)));          du(qq)=(h(qq)*max(0,SUU(qq)^z(qq)));          C1=sum(C);          d1=sum(du);    end  %for qq          %Determine the power of the penalty function        for ss=1:2*n            if DUU(ss)<1           y(ss)=1;        else           y(ss)=2;        end    %Determine the multy-stage assignment function        if DUU(ss)<=0           l(ss)=0;        elseif DUU(ss)<0.001           l(ss)=10;        elseif DUU(ss)<0.1           l(ss)=20;        elseif DUU(ss)<1           l(ss)=100;        else           l(ss)=300;        end              V(ss)=r*(l(ss)*(max(0,DUU(ss)^y(ss))));        ku(ss)=(l(ss)*(max(0,DUU(ss)^y(ss))));        C2=sum(V);        d2=sum(ku);            end  %for ss      Penalty=d1+d2;        We=Weight;    W(q) =Weight;end  %for q