一、信道估计定义
信道估计,就是从接收数据中将假定的某个信道模型的模型参数估计出来的过程。如果信道是线性的话,那么信道估计就是对系统冲激响应进行估计。需强调的是信道估计是信道对输入信号影响的一种数学表示,而“好”的信道估计则是使得某种估计误差最小化的估计算法。本文主要讲述非盲信道估计中的LS估计和MMSE估计。
二、LS估计(最小二乘法)
1.定义
LS全称为Least Square Error,即估计的信道参数与实际信道参数的差,进行平方求和后得到的误差累积最小。
2.系统模型

通信系统模型如上所示,其中 表示接收信号矢量,
表示接收信号矢量, 表示发送信号矢量,
表示发送信号矢量, 表示真实的信道模型,
表示真实的信道模型, 表示噪声矢量。
表示噪声矢量。
3.损失函数

LS估计的目标是最小化损失值,就是上式中的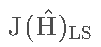 。其中,
。其中, 表示接收信号矢量,
表示接收信号矢量,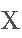 表示发送信号矢量,
表示发送信号矢量, 表示对于信道参数的估计值。
表示对于信道参数的估计值。
4.模型求解
首先,对损失函数求一阶偏导,得到



接着,令一阶偏导数为0,可以得到LS估计的最终结果如下

不难发现,LS估计的最终输出结果就是拿接收信号矢量除以发送信号矢量。
三、MMSE估计(最小均方误差)
1.定义
MMSE估计是LS估计的改进,在LS估计的最终结果 的基础上乘以加权矩阵
的基础上乘以加权矩阵 ,使之与实际信道参数更为接近。
,使之与实际信道参数更为接近。
2.系统模型
 通信系统模型与LS估计相同,其中
通信系统模型与LS估计相同,其中 表示接收信号矢量,
表示接收信号矢量, 表示发送信号矢量,
表示发送信号矢量, 表示真实的信道模型,
表示真实的信道模型, 表示噪声矢量。
表示噪声矢量。
3.损失函数

系统目标为最小化损失函数值。需要特别说明的是,也许大家会疑惑:MMSE作为一个信道估计的方法,怎么能够在估计的时候使用真实的信道参量值呢? 在知乎上,我看到了一个很好的解答:MMSE算法用于仿真环境,即信道的真实值 已知,通过LS估计求出的估计值
已知,通过LS估计求出的估计值 ,这样就可以利用真实值和估计值计算出加权矩阵
,这样就可以利用真实值和估计值计算出加权矩阵 。在实际工程应用中,先计算LS估计,然后根据实际环境选择仿真中计算所得的加权矩阵相乘,而非实际运行MMSE算法。
。在实际工程应用中,先计算LS估计,然后根据实际环境选择仿真中计算所得的加权矩阵相乘,而非实际运行MMSE算法。
4.模型求解
损失函数最小的条件为
5.模型结果

其中 为
为 与
与 的互相关矩阵,
的互相关矩阵,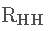 为
为 的自相关矩阵,
的自相关矩阵, 为噪声方差,
为噪声方差, 为发送信号矢量方差,
为发送信号矢量方差, 表示单位矩阵,
表示单位矩阵, 是LS估计的结果。
是LS估计的结果。
参考文章链接
信道估计–百度百科
信道估计—LS、MMSE、LMMSE准则








 本文详细介绍了通信系统中的信道估计,重点讨论了非盲信道估计中的两种重要方法——LS(最小二乘法)和MMSE(最小均方误差)估计。LS估计通过最小化估计参数与实际参数的误差平方和来求解,而MMSE估计则在LS基础上引入加权矩阵以进一步减小误差。文中还阐述了两个方法的系统模型、损失函数和求解过程,揭示了它们在实际工程应用中的不同应用场景。
本文详细介绍了通信系统中的信道估计,重点讨论了非盲信道估计中的两种重要方法——LS(最小二乘法)和MMSE(最小均方误差)估计。LS估计通过最小化估计参数与实际参数的误差平方和来求解,而MMSE估计则在LS基础上引入加权矩阵以进一步减小误差。文中还阐述了两个方法的系统模型、损失函数和求解过程,揭示了它们在实际工程应用中的不同应用场景。

















 3309
3309

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










