12.2 常数项级数审敛法

 

 

12.2 常数项级数审敛法

第二节 常数项级数的审敛法

一、正项级数及其审敛法

常数项级数的各项可以是正数、负数或零。这里我们先讨论各项都是正数或零的级数，即正项级数。正项级数非常重要，因为很多级数的收敛性问题可以归结为正项级数的收敛性问题。

设级数

是一个正项级数 (an≥0a_n \ge 0an​≥0)，它的部分和为 SnS_nSn​。显然，数列 ∣Sn∣|S_n|∣Sn​∣ 是一个单调增加数列：

如果数列 ∣Sn∣|S_n|∣Sn​∣ 有界，即 SnS_nSn​ 总不大于某一常数 MMM，根据单调有界的数列必有极限的准则，级数必收敛于和 SSS，且 S≤MS \le MS≤M。反之，如果正项级数收敛于和 SSS，即 lim⁡Sn=S\lim S_n = SlimSn​=S，则数列 ∣Sn∣|S_n|∣Sn​∣ 有界。因此，我们得到如下重要的结论：

定理 1： 正项级数收敛的充分必要条件是它的部分和数列 ∣Sn∣|S_n|∣Sn​∣ 有界。

定理 2（比较审敛法）： 设 ∑an\sum a_n∑an​ 和 ∑bn\sum b_n∑bn​ 都是正项级数，且 an≤Mbna_n \le M b_nan​≤Mbn​（n=1,2,⋯n = 1, 2, \cdotsn=1,2,⋯）。若级数 ∑bn\sum b_n∑bn​ 收敛，则级数 ∑an\sum a_n∑an​ 收敛；反之，若级数 ∑bn\sum b_n∑bn​ 发散，则级数 ∑an\sum a_n∑an​ 发散。

证： 设级数 ∑bn\sum b_n∑bn​ 收敛于和 BBB，则级数 ∑an\sum a_n∑an​ 的部分和：

二、常数项级数的推论及例子

注意到级数的每一项同乘不为零的常数 kkk 以及去掉级数前面部分的有限项不会影响级数的收敛性，我们可得如下推论：

例 1： 讨论 ppp 级数

的收敛性，其中常数 p>0p > 0p>0。

解： 设 p≤1p \le 1p≤1，这时级数的各项不小于调和级数的对应项，而调和级数发散，因此根据比较审敛法可知，当 p≤1p \le 1p≤1 时级数发散。

设 p>1p > 1p>1，因为当 k−1≤n≤kk - 1 \le n \le kk−1≤n≤k 时，有

所以级数的部分和

这表明数列 ∣Sn∣|S_n|∣Sn​∣ 有界，因此级数收敛。

综合上述结果，我们得到：ppp 级数当 p>1p > 1p>1 时收敛，当 p≤1p \le 1p≤1 时发散。

例 2： 证明级数

是发散的。

是发散的。根据比较审敛法可知所给级数也是发散的。

三、比较审敛法的极限形式

为应用上的方便，下面我们给出比较审敛法的极限形式：

定理 3（比较审敛法的极限形式）： 设 ∑an\sum a_n∑an​ 和 ∑bn\sum b_n∑bn​ 都是正项级数。

1. 

证：

1. 由极限定义可知，对于任意 ϵ>0\epsilon > 0ϵ>0，存在正整数 NNN，当 n>Nn > Nn>N 时，有

即

而级数 ∑bn\sum b_n∑bn​ 收敛，根据比较审敛法的推论，知级数 ∑an\sum a_n∑an​ 收敛。

1. 按已知条件知极限存在，如果级数 ∑an\sum a_n∑an​ 收敛，那么由结论 1 必有级数 ∑bn\sum b_n∑bn​ 收敛，但已知级数 ∑bn\sum b_n∑bn​ 发散。因此级数 ∑an\sum a_n∑an​ 不可能收敛，即级数 ∑an\sum a_n∑an​ 发散。

四、比值审敛法和根值审敛法

用比较审敛法审敛时，需要适当地选取一个已知其收敛性的级数作为比较的基准。最常选用作基准级数的是等比级数和 ppp 级数。将所给正项级数与等比级数比较，我们能得到在实用上很方便的比值审敛法和根值审敛法。

定理 4（比值审敛法，达朗贝尔(d'Alembert) 判别法）： 设 ∑an\sum a_n∑an​ 为正项级数，如果

那么当 p<1p < 1p<1 时级数收敛；p>1p > 1p>1（或 lim⁡n→∞an+1an=+∞\lim_{n \to \infty} \frac{a_{n+1}}{a_n} = +\inftylimn→∞​an​an+1​​=+∞）时级数发散；p=1p = 1p=1 时级数可能收敛也可能发散。

证：

1. 当 p<1p < 1p<1 时，取一个适当小的正数 ϵ\epsilonϵ，使得 p+ϵ=r<1p + \epsilon = r < 1p+ϵ=r<1。根据极限定义，存在正整数 MMM，当 n≥Mn \ge Mn≥M 时，有不等式

因此

而级数 ∑an\sum a_n∑an​ 收敛（公比 r<1r < 1r<1），根据定理 2 的推论，知级数 ∑an\sum a_n∑an​ 收敛。

1. 当 p>1p > 1p>1 时，取一个适当小的正数 ϵ\epsilonϵ，使得 p−ϵ>1p - \epsilon > 1p−ϵ>1。根据极限定义，当 n≥Mn \ge Mn≥M 时有不等式

也就是

所以当 n≥Mn \ge Mn≥M 时，级数的一般项 ana_nan​ 是逐渐增大的，从而 lim⁡an≠0\lim a_n \ne 0liman​=0。根据级数收敛发散的必要条件可知级数 ∑an\sum a_n∑an​ 发散。

1. 当 p=1p = 1p=1 时级数可能收敛也可能发散。例如 ppp 级数，不论 ppp 为何值都有 lim⁡an+1an=1\lim \frac{a_{n+1}}{a_n} = 1liman​an+1​​=1，但我们知道，当 p>1p > 1p>1 时级数收敛，当 p≤1p \le 1p≤1 时级数发散，因此只根据 p=1p = 1p=1 不能判定级数的收敛性。

例 4： 证明级数

是收敛的，并估计以级数的部分和 SnS_nSn​ 近似代替和 SSS 所产生的误差。

解： 因为

根据比值审敛法可知所给级数收敛。

用这个级数的部分和 SnS_nSn​ 近似代替和 SSS 所产生的误差为

因为

因此

由此可见，用部分和 SnS_nSn​ 近似代替和 SSS 所产生的误差随 nnn 的增大而迅速减小。

例 5： 判定级数

的收敛性。

解： 因为

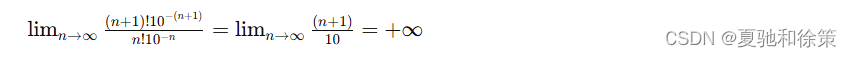
根据比值审敛法可知所给级数发散。

定理 5（根值审敛法，柯西判别法）： 设 ∑an\sum a_n∑an​ 为正项级数，如果

定理 5 的证明与定理 4 相仿，这里从略。

例 6： 判定级数

的收敛性。

证： 因为

根据根值审敛法知所给级数收敛。

五、极限审敛法

将所给正项级数与 ppp 级数作比较，可得在实用上较方便的极限审敛法。

定理 6（极限审敛法）： 设 ∑an\sum a_n∑an​ 为正项级数。

1. 

证：

1. 

例 7： 判定级数

的收敛性。

解： 因为

根据极限审敛法，知所给级数收敛。

例 8： 判定级数

的收敛性。

解： 因为

根据极限审敛法，知所给级数收敛。

 

二、交错级数及其审敛法

所谓交错级数是这样的级数，它的各项是正负交错的，从而可以写成下面的形式：

定理 7（莱布尼茨定理）

如果交错级数满足以下条件：

1. 

那么级数收敛，且其和 S≤u1S \le u_1S≤u1​，其余项 rnr_nrn​ 的绝对值 ∣rn∣≤un+1|r_n| \le u_{n+1}∣rn​∣≤un+1​。

证明：

首先证明前 2n2n2n 项的和 S2nS_{2n}S2n​ 的极限存在。为此把 S2nS_{2n}S2n​ 写成两种形式：

根据条件 (1) 知道

所有括号中的差都是非负的。由第一种形式可见数列 S2nS_{2n}S2n​ 是单调增加的，由第二种形式可见 S2n≤u1S_{2n} \le u_1S2n​≤u1​。于是，根据单调有界数列必有极限的准则知道，当 nnn 无限增大时，S2nS_{2n}S2n​ 趋于一个极限 SSS，并且：

再证明前 2n+12n+12n+1 项的和 S2n+1S_{2n+1}S2n+1​ 的极限也是 SSS。事实上，我们有：

由条件 (2) 知 lim⁡n→∞u2n+1=0\lim_{n \to \infty} u_{2n+1} = 0limn→∞​u2n+1​=0，因此：

由于级数的前偶数项的和与奇数项的和趋于同一极限 SSS，故级数：

的部分和 SnS_nSn​ 当 n→∞n \to \inftyn→∞ 时具有极限 SSS。这就证明了级数：

收敛于和 SSS，且 S≤u1S \le u_1S≤u1​。

最后，不难看出余项 rnr_nrn​ 可以写成：

其绝对值：

上式右端也是一个交错级数，它也满足收敛的两个条件，所以其和小于级数的第一项，也就是说：

证明完毕。

例如，交错级数：

满足条件：

1. 

所以它是收敛的，且其和 S≤1S \le 1S≤1。如果取前 nnn 项的和：

作为 SSS 的近似值，所产生的误差：

随着 nnn 的增加而减小。

 

三、绝对收敛与条件收敛

现在我们讨论一般的级数：

它的各项为任意实数。如果级数各项的绝对值所构成的正项级数 ∑∣an∣\sum |a_n|∑∣an​∣ 收敛，那么称级数绝对收敛；如果级数收敛，而 ∑∣an∣\sum |a_n|∑∣an​∣ 发散，那么称级数是条件收敛。容易知道，绝对收敛的级数必定收敛。

定理 8

如果级数绝对收敛，那么级数必定收敛。

证明：

令

由收敛级数的基本性质可知：

所以级数 ∑an\sum a_n∑an​ 收敛。定理证毕。

上述证明中引入的级数：

是把级数 ∑an\sum a_n∑an​ 中的负项换成 0 而得的，它也就是级数中的全体正项所构成的级数。类似地可知，令：

则为级数 ∑an\sum a_n∑an​ 中全体负项的绝对值所构成的级数。如果级数 ∑an\sum a_n∑an​ 绝对收敛，那么级数 ∑vn\sum v_n∑vn​ 和 ∑wn\sum w_n∑wn​ 都收敛；如果级数 ∑an\sum a_n∑an​ 条件收敛，而 ∑∣an∣\sum |a_n|∑∣an​∣ 发散，那么级数 ∑vn\sum v_n∑vn​ 和 ∑wn\sum w_n∑wn​ 都发散。

定理 8 说明，对于一般的级数 ∑an\sum a_n∑an​，如果我们用正项级数的审敛法判定级数 ∑∣an∣\sum |a_n|∑∣an​∣ 收敛，那么此级数 ∑an\sum a_n∑an​ 收敛。这就使得一大类级数的收敛性判定问题转化成为正项级数的收敛性判定问题。

例 9：判定级数 的收敛性

解： 因为

例 10：判定级数 ​ 的收敛性

解： 这是一个交错级数，满足条件：

根据莱布尼茨定理，这个级数收敛，但不是绝对收敛，因为：

而级数 ​ 是发散的。所以该级数是条件收敛的。

 

 

 

四、绝对收敛级数的性质

绝对收敛级数具有许多条件收敛级数所没有的性质，下面给出关于绝对收敛级数的两个性质。

定理 9

绝对收敛级数经改变项的位置后构成的级数也收敛，且与原级数有相同的和（即绝对收敛级数具有可交换性）。

证明：

1. 先证定理对于收敛的正项级数是正确的。 设级数

为收敛的正项级数，其部分和为 SnS_nSn​，和为 SSS。并设级数

为改变项的位置后构成的级数，其部分和为 S′S'S′。

对于任何 nnn，当它固定后，取 mmm 足够大，使 uk1,uk2,⋯ ,uknu_{k1}, u_{k2}, \cdots, u_{kn}uk1​,uk2​,⋯,ukn​ 各项都出现在

中，于是得

所以，单调增加的数列 Sm′S'_mSm′​ 不超过定数 SSS，根据单调有界数列必有极限的准则，可知

另一方面，如果把原来的级数看成是级数改变项的位置以后所成的级数，那么应用刚才证得的结论，又有

要使得上面两个不等式同时成立，必定有

1. 再证定理对一般的绝对收敛级数是正确的。 设级数 ∑an\sum a_n∑an​ 绝对收敛。在定理 8 的证明中已得

而 ∑an+\sum a_n^+∑an+​ 和 ∑an−\sum a_n^-∑an−​ 是收敛的正项级数。故有

若级数改变项的位置后的级数分别为 ∑akn+\sum a_{kn}^+∑akn+​ 和 ∑akn−\sum a_{kn}^-∑akn−​，由(1)证得的结论可知

所以

定理证毕。

定理 10（绝对收敛级数的乘法）

设级数 ∑an\sum a_n∑an​ 和 ∑bn\sum b_n∑bn​ 都绝对收敛，其和分别为 SSS 和 TTT，则它们的柯西乘积

也是绝对收敛的，且其和为 STSTST。

证明：

考虑把级数 ∑cn\sum c_n∑cn​ 的括号去掉后所成的级数

如果级数 ∑cn\sum c_n∑cn​ 绝对收敛且其和为 WWW，那么由收敛级数的基本性质及比较审敛法可知，级数 ∑cn\sum c_n∑cn​ 也绝对收敛且其和为 WWW。因此只要证明级数 ∑cn\sum c_n∑cn​ 绝对收敛且其和 W=STW = STW=ST 就行了。

1. 先证级数 ∑cn\sum c_n∑cn​ 绝对收敛。

设 WmW_mWm​ 为级数 ∑cn\sum c_n∑cn​ 的前 mmm 项分别取绝对值后所作成的和，又设

则显然有

由此可见单调增加数列 WmW_mWm​ 不超过定数 ABABAB，所以级数 ∑cn\sum c_n∑cn​ 绝对收敛。

1. 再证级数 ∑cn\sum c_n∑cn​ 的和 W=STW = STW=ST。

把级数 ∑cn\sum c_n∑cn​ 的各项位置重新排列并加上括号使它成为按“正方形法”排列所组成的级数

根据定理 9 及收敛级数的基本性质可知，对于绝对收敛级数 ∑cn\sum c_n∑cn​ 这样做法是不会改变其和的。容易看出，级数的前 nnn 项的和恰好为

所以

定理证毕。