1. 变换群(Group)
(a) 相似性变换:圆仍然是圆,正方形仍然是正方形,直线的平行和垂直属性也被保持
(b) 仿射变换:圆形变为椭圆,垂直线不再垂直,而平行线仍然平行
(c) 投影变换:平行线不再平行,近大远小
上图可以看到不同层次的变换,这些变换构成一个变换群,按不同层次包括:
- 通用线性群GL(n):可逆n×n实数矩阵
- 投影线性群PL(n):GL(n)的商群
- 仿射群(affine group):PL(3)的子群,其最后一行为(0,0,1)
- 欧式群(Euclidean group):仿射群的子群,左上角的2×2子阵为正交阵。
- 有向欧式群(oriented Euclidean group):欧式群的子群,左上角的2×2子阵的行列式为1。
有些变换不是群,如透视变换,因为两个透视变换的组合是一个投影变换,而不再是透视。
某些几何属性对于某些变换具有不变性。例如:两点可分离,对于欧式变换(平移+旋转)是不变的,而对于相似性变换(平移+旋转+等方性缩放)则不是不变的。距离是欧式不变的,但不是相似性不变的。角度则对欧式变换和相似性变换都是不变的。
2. 等距变换(isometry = iso(相等) + metric(度量))
等距变换在平面变换中保持欧式距离不变。它可以表示为

其中є=±1. 如果є=1,则保持方向不变,是一个欧式变换(平移+缩放)。如果є=-1,则为反向等距变换,代表欧式变换+反射(diag(-1,1,1))。欧式变换构成一个群,反向等距变换不构成群。
其中R是一个2×2选择矩阵,它是个正交阵,即RTR =RRT =I。t 是一个平移2维向量。欧式变换也叫做位移(displacement),它有3个自由度(1个旋转,2个平移),因此可由两对匹配点确定。
等距变换具有对长度、角度和面积的不变性。
3. 相似性变换
相似性变换 = 等距变换 + 等方性缩放,用矩阵表示为:
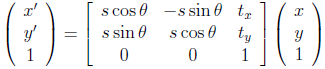
其中因子 s 表示等方性缩放。
相似性变换保持形状不变。平面相似性变换具有4个自由度,比欧式变换多一个比例因子。
相似性变换对如下属性具有不变性:角度,平行,长度比例,面积比例。
4. 仿射变换(affinity)
仿射变换 = 非奇异线性变换 + 平移,用矩阵表示为:
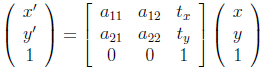
平面仿射变换具有6个自由度,可由3对匹配点对确定。
其中非奇异矩阵A可通过SVD分解,得到:
A = UDVT = (UVT)(VDVT) = R(θ)R(-Ф)DR(Ф)
这表示 A 变换可以等效为如下过程:首先对坐标进行 Ф 角度旋转,然后分别在旋转后的 x 和 y 坐标方向进行比例为 λ1 和 λ2 的缩放,然后再旋转回去,最后再进行 θ 角度旋转。
仿射变换对如下属性具有不变性:平行线,平行线段的长度比例,面积比例。而对长度比例和角度没有不变性。
5. 投影变换
投影变换是一种齐次坐标下的非奇异线性变换,它的矩阵形式为:

它有9个自由度,但只有比例意义,因此它可由8个参数定义。两个平面之间的投影变换可以由4对匹配点(其中一个平面上的任意3点不共线)决定。
投影变换最基本的不变性是互比例(cross ratio),即4个共线点之间的比例的比例。
投影变换的分解:投影变换可分解为相似性变换 HS 、仿射变换 HA 和投影变换 HP的级联,即
或者
投影变换分解的意义在于可以简化算法。例如,当仅仅想在一幅投影平面上测量长度比例时,则只要对该图像进行HP和HA的校正就够了,因为相似性变换HS对长度比例具有不变性。
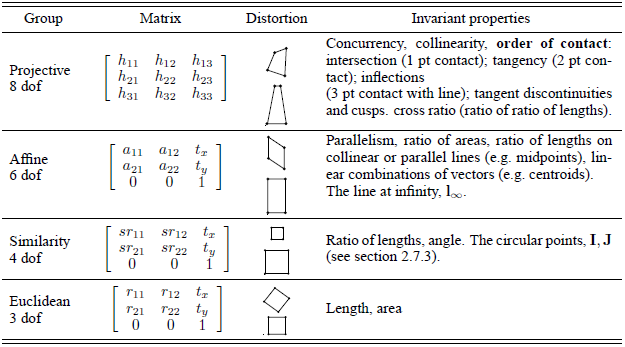
6. 总结










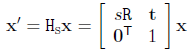


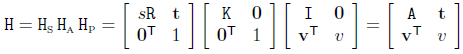
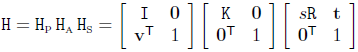
















 3440
3440

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








