数据结构——掌握求解活动的最早（晚）开始时间

如图所示AOE网表示一项包含8个活动的工程，针对下图进行分析：

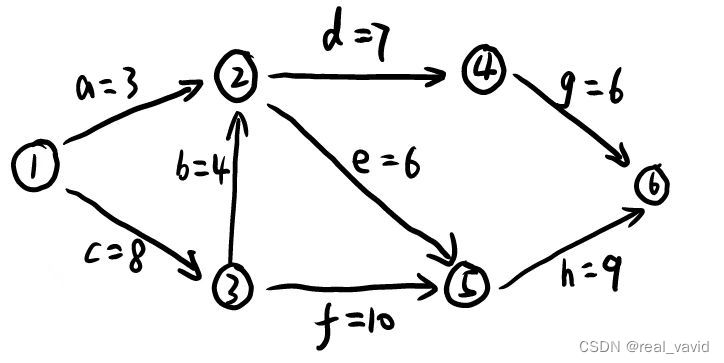
方法一：分别求事件和活动

事件是点，活动是边

求事件的最早开始时间，顺推，二者取最大；
求事件的最晚开始时间，逆推，二者取最小。

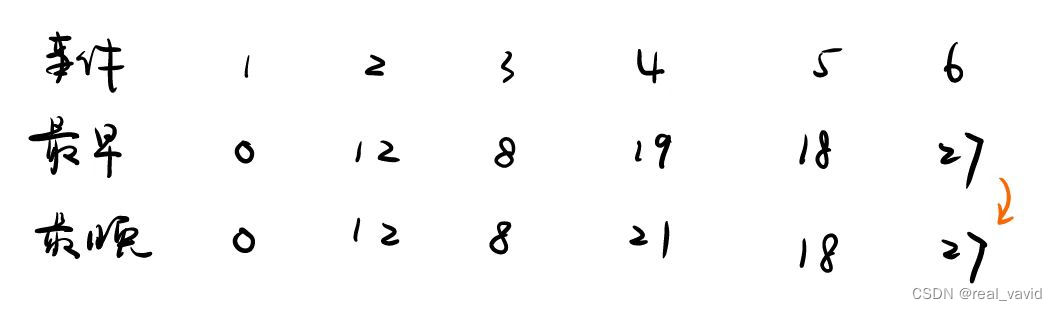
根据事件的最早开始时间和最晚开始时间求活动的最早开始时间和最晚开始时间：
活动的最早开始时间 = 前一个事件的最早开始时间
活动的最晚开始时间 = 后一个时间的最晚开始时间 - 当前活动的时间

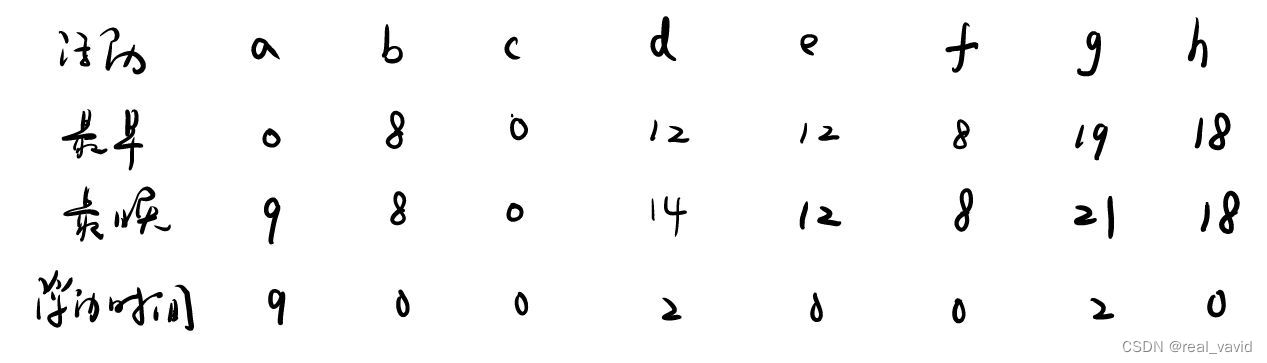
方法二：七格图法

绘制活动，顺推依次算出EF，最终得出工期
相关公式（ES从第0天开始）
最早开始及最早完成（顺推）：
最早开始ES = 取最大值（前置活动的最早完成EF）；
最早完成EF = 最早开始ES + 持续时间DU

最早开始时间，顺推选最大（因为只有前置活动全部完成才能开始下一个活动）;

逆推，得出活动最晚开始时间和总浮动时间
从右至左，最后一个活动完成：最早的完成时间 = 最晚完成时间 = 工期
然后依次算出 LS 和 TF，最终得出关键路径

相关公式（最后一个活动的LF = 最后一个活动的EF = 工期 ）
最晚完成LF = 取最小值（后续活动的LS）
最晚开始LS = 最晚完成LF - 持续时间DU

最晚完成时间，逆推选最小（同理，因为只有前置活动全部完成才能开始下一个活动）;

顺推，得出最早开始时间和最早完成时间，如下图

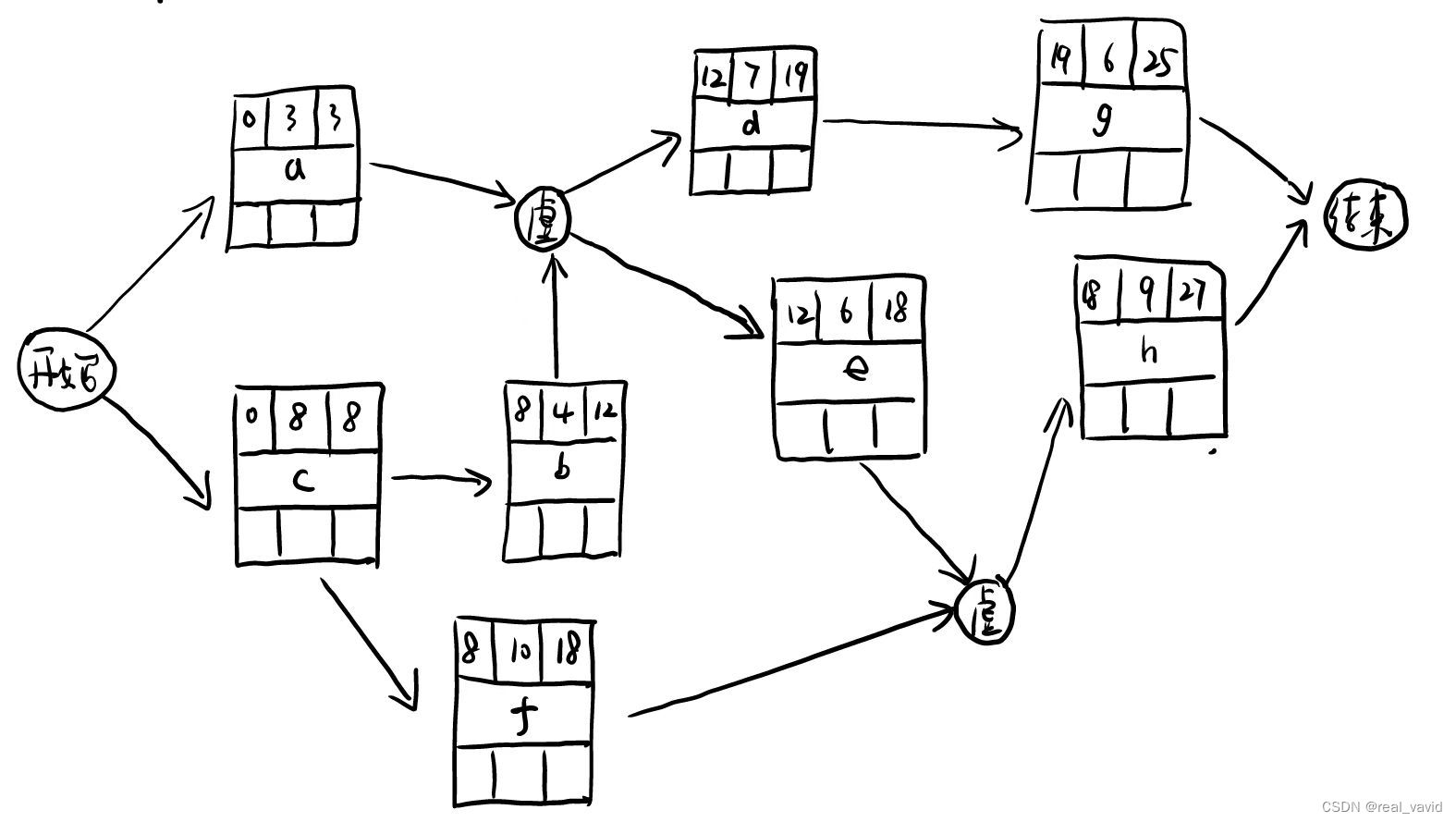
逆推，得出最晚完成时间和最晚开始时间，如下图（蓝色标记）：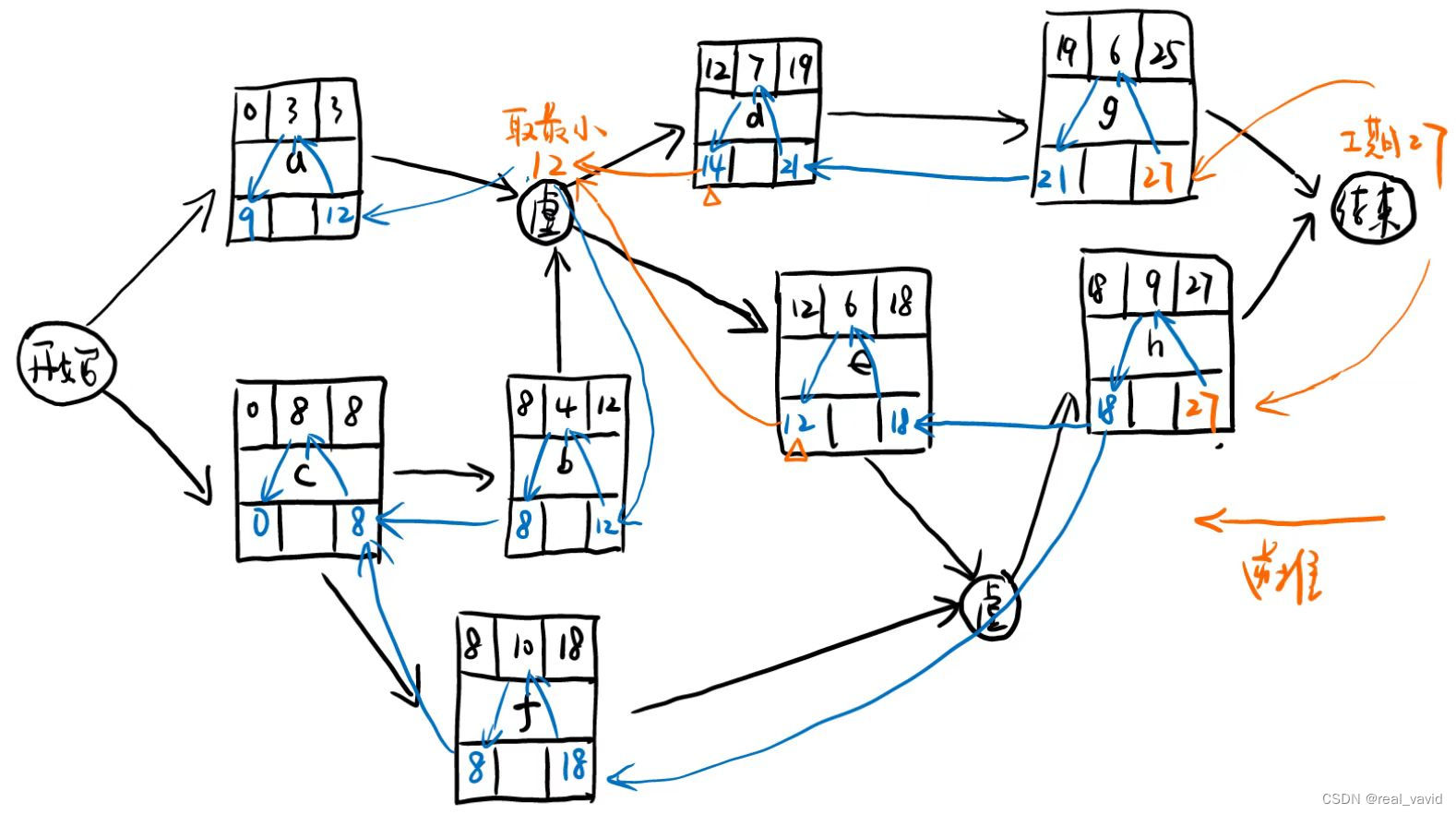
进而，得出浮动时间，如下图（绿色标记）：

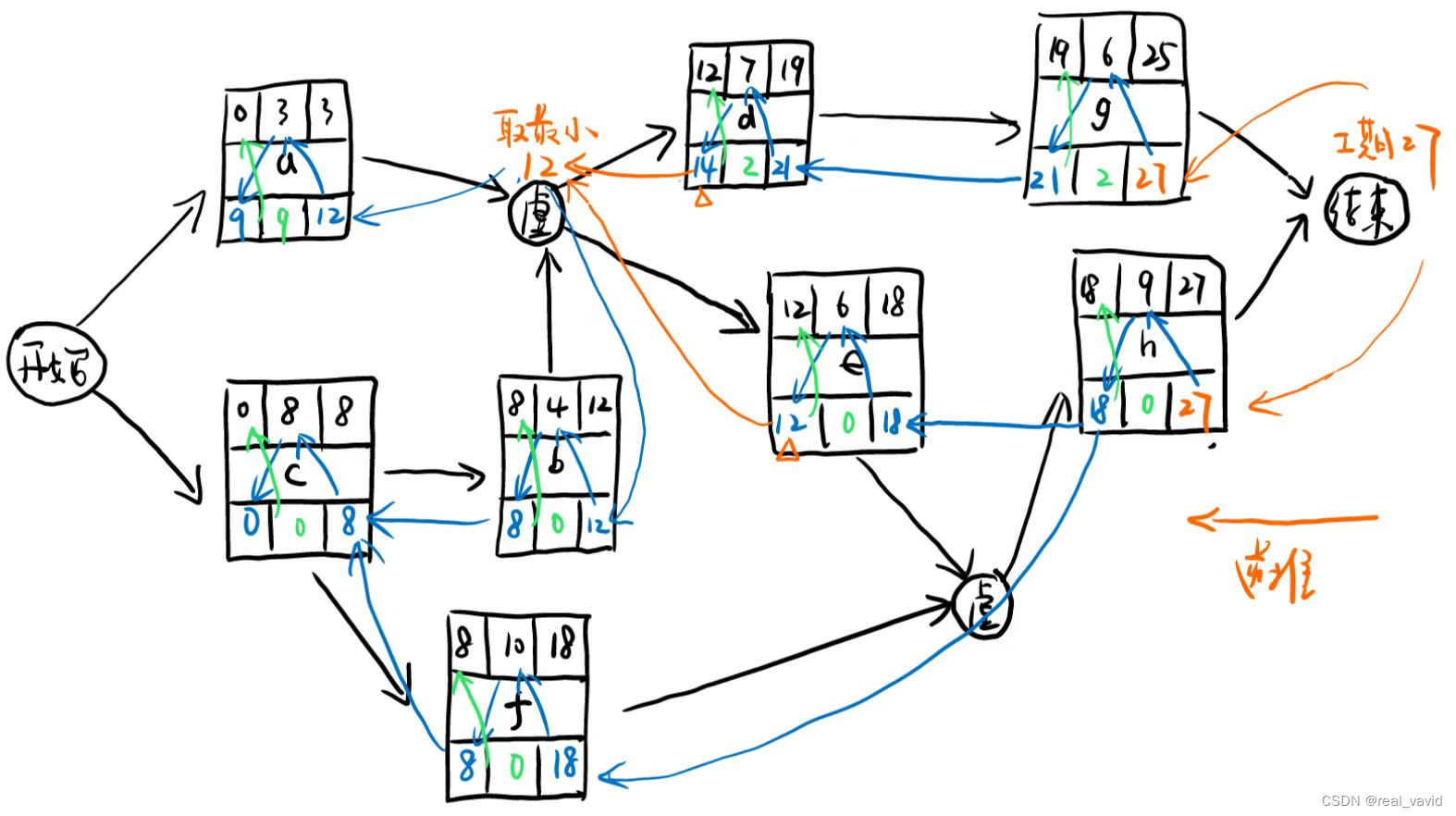
最后，根据浮动时间为0的活动，得出关键路径，如下图：

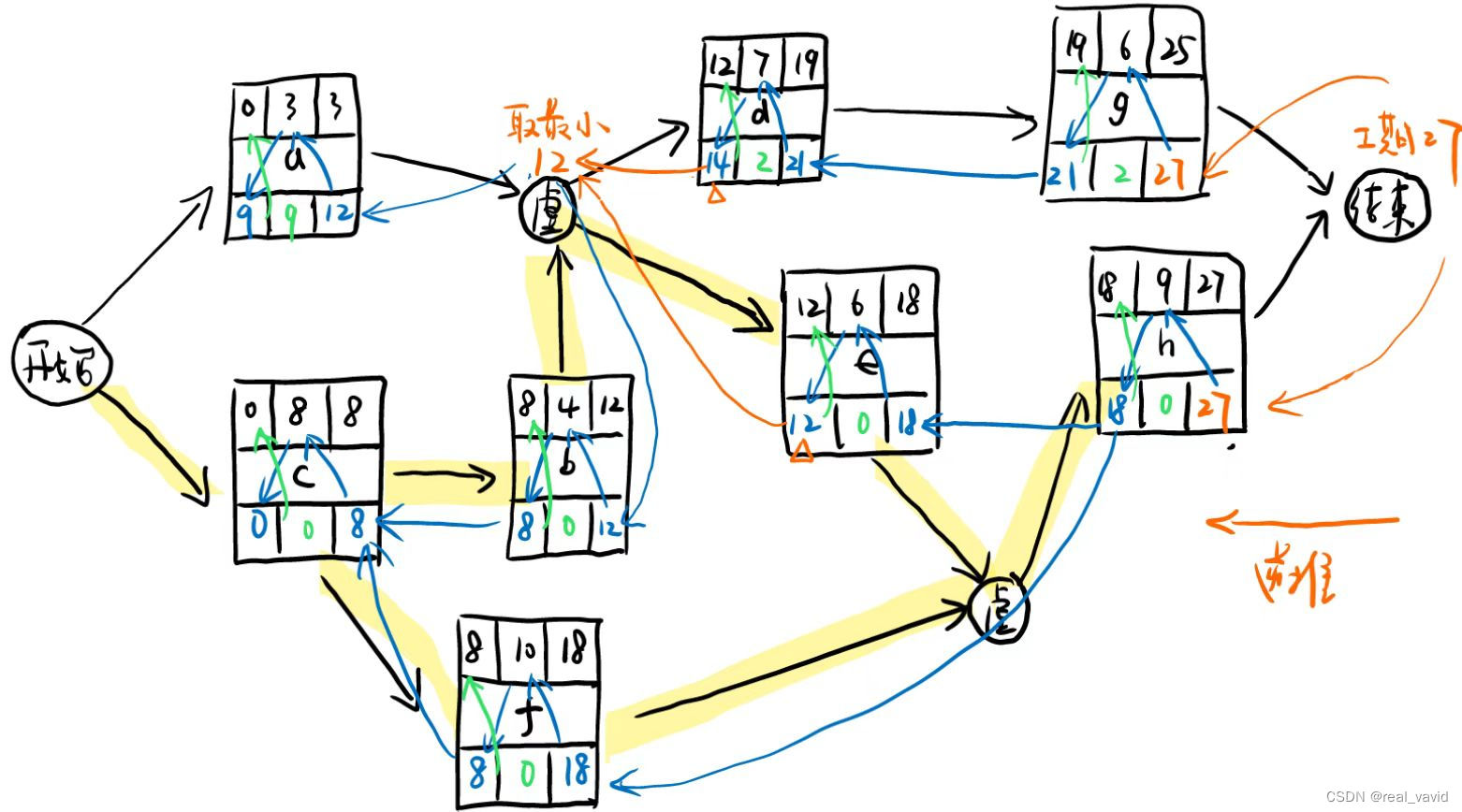
关键路径有两条：
c->b->e->h
c->f->h