十二、单力臂机械臂的鲁棒自适应控制
通过引入直接自适应控制的思想,采用基于Lyapunov直接法的鲁棒模型参考自适应控制方法,可以在具有参数不确定性和未知非线性摩擦特性的情况下,使跟踪误差趋于零,其优点在于不需要建立摩擦模型,不需要精确的摩擦参数,而只需要动、静摩擦的上界值。
12.1 问题描述
不确定单机械臂为
其中为系统输出转角,
为转动惯量,
为重力,
为控制输入,
为未知的非线性摩擦,质心距连杆的转动中心为
,连杆运动的黏性摩擦系数为
,
为黏性摩擦系数的不确定值,
为弹性摩擦系数。
如果机械臂的运动平面与水平面平行,则机器人运动方程中的重力项可忽略。则上式变为
不确定单机械臂可采用二阶微分方程来描述:
其中;
为非负的有界实数,
为正实数。
的数学描述如下:

其中为开关函数,定义如下:
和
分别为静摩擦和库仑摩擦的变化函数,假定
和
为未知函数,但是有界的,即存在正实数
和
,使得
引入稳定的参考模型如下:
其中为模型输出,
为系统指令输入,
为正实数。
定义误差信号为
则控制的问题在于,寻求控制,使得对于任意初态,跟踪误差
满足
12.2 鲁棒模型参考自适应控制
由上式得到误差的动态方程如下:
即
定义向量,则得到上式的状态空间表达形式为
其中,
,
。
由于矩阵的特征值具有负实部,系统是渐进稳定的, 则存在正定矩阵
和
,使得下式成立,
定义辅助信号为
由辅助信号,取控制律式
其中为待调节的增益系数,
为摩擦环节的鲁棒补偿项。
-
定理
设计增益系数自适应律和鲁棒补偿项设计为
其中为符号函数,
为正实数,那么对于任意的
,
及任意的初始条件,误差
是有界的且渐进收敛于0。
12.3 仿真实例
被控对象的动态方程为
其中。
非线性摩擦的上界值及分别取为
对象的非线性摩擦模型为
参考模型取,
,即模型参数为
。
令,求解Lyapunov方程得
,则辅助信号表示为
12.4 仿真结果
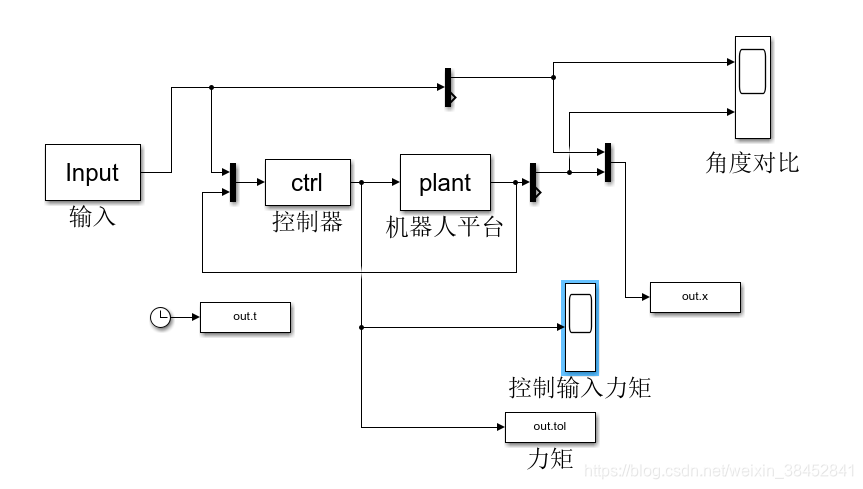
图1 simulink仿真图

图1 参考模型轨迹和实际模型轨迹对比

图2 控制输出力矩
























 1940
1940

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








