SLAM【十】回环检测

回环检测的作用及意义

作用

问题：为了解决整个SLAM出现的累计误差，导致无法构建全局一致的轨迹和地图。
回环检测的关键在于如何有效的检测出相机经过同一个地方

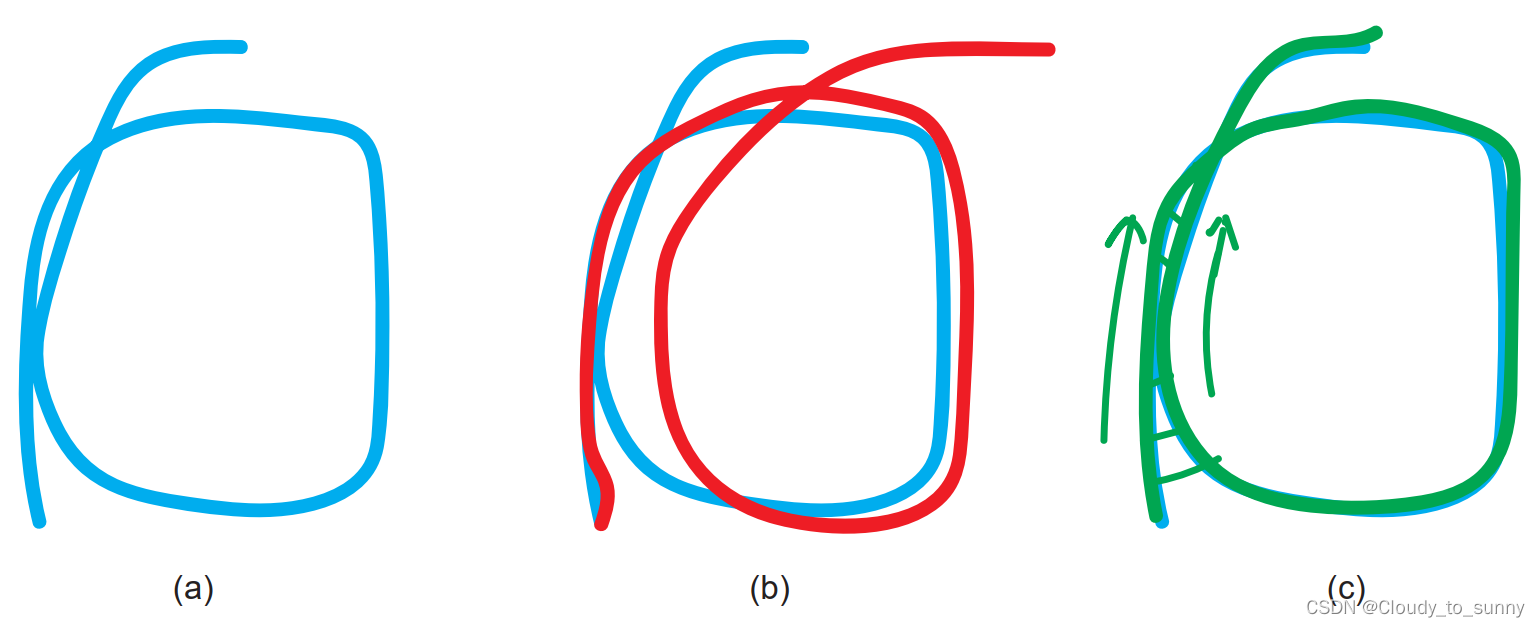
（a）真实轨迹；（b）由于前端只给出相邻帧间的估计，优化后的Pose Graph 出现漂移；（c）添加回环检测后的 Pose Graph 可以消除累积误差。

意义

1. 关系到估计的轨迹和地图在长时间下的正确性、
2. 能够提高当前数据与所有历史数据的关联，从而可以利用回环检测进行重定位

重定位：确定自身在已经走过的轨迹并建图的场景中的位置。

回环检测方法

基于外观的回环检测方法，与前端和后端都无关，仅根据两幅图像的相似性确定回环检测的关系。该方法的核心问题为：如何计算图像间的相似性

对于图像$A$和图像$B$，记它们之间的相似性评分：s($A,B$)大于一定量后，我们认为出现了一个回环。
出现问题：
图像可以表示成矩阵，如果直接使用矩阵相减，然后取某一种范数，像这样：

$$s(\mathbf{A},\mathbf{B})=\Vert \mathbf{A}-\mathbf{B}\Vert$$

这样做的缺点：

1. 像素灰度是一种不稳定的测量值，严重受环境光照和相机曝光的影响。对于同样的数据，也可能得到一个很大的差异值。
2. 当相机视角发生少量变化时，即使每个物体的光度不变，它们的像素也会在图像中发生位移，造成一个很大的差异值。

所以做差并求范数这种方式不能很好地反映图像间的相似关系。

准确率和召回率

算法/事实	是回环	不是回环
是回环	真阳性(TP)	假阳性(FP)
不是回环	假阴性(FN)	真阴性(TN)

假阳性（False Positive）又称感知偏差，而假阴性（False Negative）称为感知变异。
对于某种特定算法，可以统计它在某个数据集上的TP、TN、FP、FN的出现次数，理想的算法希望TP和TN高，而FP和FN低。

准确率： Precision = TP/(TP+FP)
召回率： Recall = TP/(TP+FN)

准确率：算法提取的所有回环中，确实是真实回环的概率。
召回率：在所有真实回环中，被正确检测出来的概率。

这两个统计量有一定的代表性，并且通常来说是一个矛盾

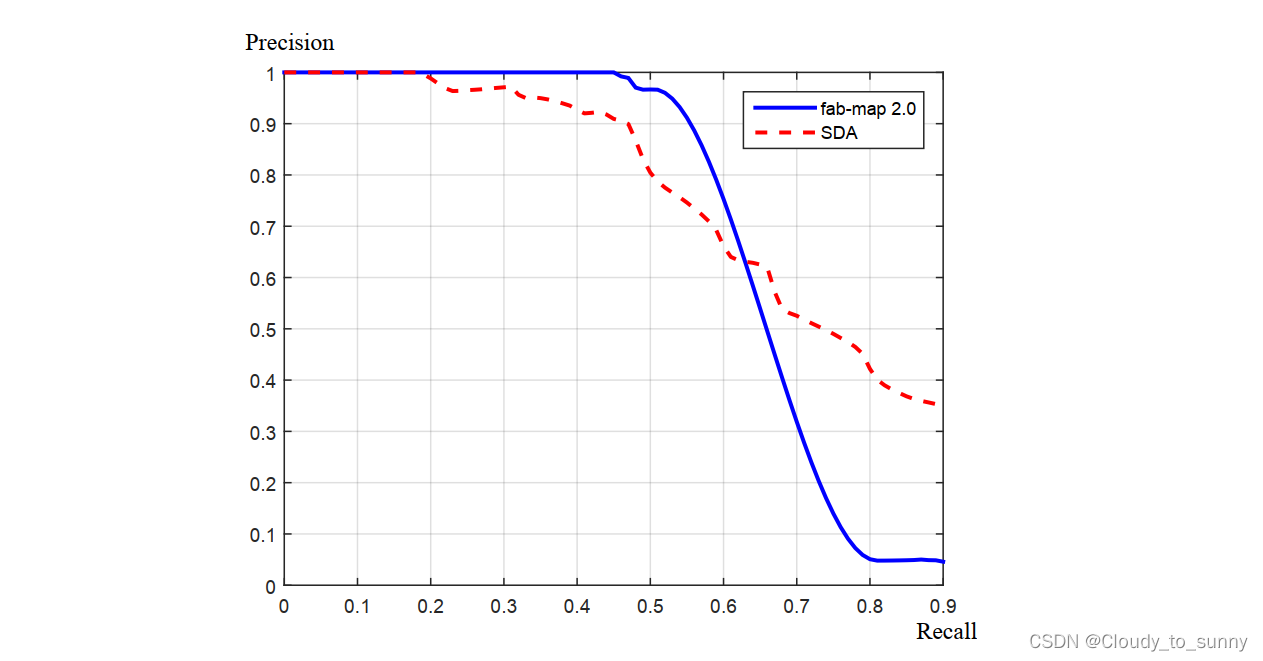
为了评价算法的好坏，我们会测试它在各种配置下的 P 和 R 值，然后做出一条Precision-Recall 曲线。当用召回率为横轴，用准确率为纵轴时，我们会关心整条曲线偏向右上方的程度、 100% 准确率下的召回率，或者 50% 召回率时候的准确率，作为评价算法的指标。

在 SLAM 中，我们对准确率要求更高，而对召回率则相对宽容一些。由于假阳性的（检测结果是而实际不是的）回环将在后端的 Pose Graph 中添加根本错误的边，有些时候会导致优化算法给出完全错误的结果。相比之下，召回率低一些，则顶多有部分的回环没有被检测到，地图可能受一些累积误差的影响——然而仅需一两次回环就可以完全消除它们了。所以说在选择回环检测算法时，我们更倾向于把参数设置地更严格一些，或者在检测之后再加上回环验证的步骤。

前面使用的做差然后求范数的方法，准确率和召回率都不高，所以舍弃。

词袋模型

不使用像前端那样的特征匹配的原因：特征的匹配会比较费时、当光照变化时特征描述可能不稳定。

词袋，也就是 Bag-of-Words（BoW），目的是用“图像上有哪几种特征”来描述一个图像。例如，如果某个照片，我们说里面有一个人、一辆车；而另一张则有两个人、一只狗。根据这样的描述，可以度量这两个图像的相似性。
具体步骤：

1. 确定“人、车、狗”等概念——对应于 BoW 中的“单词”（Word），许多单词放在一起，组成了“字典”（Dictionary）。
2. 确定一张图像中，出现了哪些在字典中定义的概念——我们用单词出现的情况（或直方图）描述整张图像。这就把一个图像转换成了一个向量的描述。
3. 比较上一步中的描述的相似程度。

首先我们通过某种方式，得到了一本“字典”。字典上记录了许多单词，每个单词都有一定意义，例如“人”、“车”、“狗”都是记录在字典中的单词，我们不妨记为 $w_1,w_2,w_3$。一张图片可以表示为：
$$A=1\cdot w_1+1\cdot w_2+0\cdot w_3$$
用向量$[1,1,0{]}^T$表示图片A，也可以说"1"表示有，"0"表示无，或者"1"表示有1个，"0"表示有0个。

通过字典和单词，只需一个向量就可以描述整张图像了。该向量描述的是“图像是否含有某类特征”的信息，比单纯的灰度值更加稳定。又因为描述向量说的是“是否出现”，而不管它们“在哪儿出现”，所以与物体的空间位置和排列顺序无关，因此在相机发生少量运动时，只要物体仍在视野中出现，我们就仍然保证描述向量不发生变化。 ‹ 基于这种特性，我们称它为Bag-of-Words 而不是什么 List-of-Words，强调的是 Words 的有无，而无关其顺序。因此，可以说字典类似于单词的一个集合。

设计一定的计算方式，就能确定图像间的相似性

$$s(\mathbf{a},\mathbf{b})=1-\frac{1}{W}\Vert \mathbf{a}-\mathbf{b}{\Vert }_1$$

其中范数取 L1 范数，即各元素绝对值之和。请注意在两个向量完全一样时，我们将得到 1；完全相反时（a 为 0 的地方 b 为 1）得到 0。这样就定义了两个描述向量的相似性，也就定义了图像之间的相似程度。

字典

字典的结构

字典生成问题类似于一个聚类问题。聚类问题是无监督机器学习（Unsupervised ML）中一个特别常见的问题，用于让机器自行寻找数据中的规律的问题。 BoW 的字典生成问题亦属于其中之一。

当有$N$个数据，想要归成k个类，使用K-means的步骤：

1. 随机选取 k 个中心点： $c1,...,c_k$。
2. 对每一个样本，计算与每个中心点之间的距离，取最小的作为它的归类。
3. 重新计算每个类的中心点。
4. 如果每个中心点都变化很小，则算法收敛，退出；否则返回 1。

问题：如何根据图像中某个特征点，查找字典中相应的单词？
$k$叉树
假设有$N$个特征点，希望构建一个深度为d、每次分叉为$k$d的树，步骤：

1. 在根节点，用 k-means 把所有样本聚成 k 类（实际中为保证聚类均匀性会使用
   k-means++）。这样得到了第一层。
2. 对第一层的每个节点，把属于该节点的样本再聚成 k 类，得到下一层。
3. 依此类推，最后得到叶子层。叶子层即为所谓的 Words。

实际上，最终我们仍在叶子层构建了单词，而树结构中的中间节点仅供快速查找时使用。这样一个 k 分支，深度为 d 的树，可以容纳 kd 个单词。另一方面，在查找某个给定特征对应的单词时，只需将它与每个中间结点的聚类中心比较（一共 d 次），即可找到最后的单词，保证了对数级别的查找效率。

字典的创建

训练字典就像机器学习根据数据集进行训练一样，这里使用 的是 BoW库，这里使用的是DBoW3，具体库下载在Github上，按照cmake流程对它进行编译和安装
训练字典：

#include "DBoW3/DBoW3.h"
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/features2d/features2d.hpp>
#include <iostream>
#include <vector>
#include <string>

using namespace cv;
using namespace std;

/***************************************************
 * 本节演示了如何根据data/目录下的十张图训练字典
 * ************************************************/

int main( int argc, char** argv ) {
    // read the image 
    cout<<"reading images... "<<endl;
    vector<Mat> images; 
    for ( int i=0; i<10; i++ )
    {
        string path = "./data/"+to_string(i+1)+".png";
        images.push_back( imread(path) );
    }
    // detect ORB features
    cout<<"detecting ORB features ... "<<endl;
    Ptr< Feature2D > detector = ORB::create();
    vector<Mat> descriptors;
    for ( Mat& image:images )
    {
        vector<KeyPoint> keypoints; 
        Mat descriptor;
        detector->detectAndCompute( image, Mat(), keypoints, descriptor );
        descriptors.push_back( descriptor );
    }
    
    // create vocabulary 
    cout<<"creating vocabulary ... "<<endl;
    DBoW3::Vocabulary vocab;
    vocab.create( descriptors );
    cout<<"vocabulary info: "<<vocab<<endl;
    vocab.save( "vocabulary.yml.gz" );
    cout<<"done"<<endl;
    
    return 0;
}

相似度计算

由于有些单词对图像描述的作用不同，有的作用较大，比如“文档、足球”，有的作用不大，比如“的，是”，因此希望对单词的区分性或重要性加以评估，给他们不同的权重以起到更好的效果。
TF-IDF(Term Frequency-Inverse Document Frequency)，或译频率-逆文档频率，是文本检索中常用的一种加权方式，也用于BoW模型中。TF 部分的思想是，某单词在一个图像中
经常出现，它的区分度就高。另一方面， IDF 的思想是，某单词在字典中出现的频率越低，
则分类图像时区分度越高。

我们统计某个叶子节点 $w_i$ 中的特征数量相对于所有特征数量的比例，作为 IDF 部分。假设所有特征数量为 $n,w_i$ 数量为$n_i$，那么该单词的 IDF 为：
$${\mathrm{I}\mathrm{D}\mathrm{F}}_i=\log \frac{n}{n_i}$$

TF 部分则是指某个特征在单个图像中出现的频率。假设图像 A 中，单词$w_i$ 出现了 $n_i$ 次，而一共出现的单词次数为 $n$，那么 TF 为：

$${\mathrm{T}\mathrm{F}}_i=\frac{n_i}{n}$$
$w_i$的权重等于TF乘IDF之积：

$${\eta }_i={\mathrm{T}\mathrm{F}}_i\times {\mathrm{I}\mathrm{D}\mathrm{F}}_i$$

考虑权重后，对于谋福图像A，它的特征点可队以可对应到许多个单词，组成它的BoW为：
η i = T F i × I D F i A = { ( w 1 , η 1 ) , ( w 2 , η 2 ) , … , ( w N , η N ) } ≜ v A \eta_{i}=\mathrm{TF}_{i} \times \mathrm{IDF}_{i}A=\left\{\left(w_{1}, \eta_{1}\right),\left(w_{2}, \eta_{2}\right), \ldots,\left(w_{N}, \eta_{N}\right)\right\} \triangleq \boldsymbol{v}_{A} ηi​=TFi​×IDFi​A={(w1​,η1​),(w2​,η2​),…,(wN​,ηN​)}≜vA​

计算两张图片AB的相似度：
$L_1$范数形式：

$$s\left({\mathbf{v}}_A-{\mathbf{v}}_B\right)=2\sum _{i=1}^N\left|{\mathbf{v}}_{A_i}\right|+\left|{\mathbf{v}}_{B_i}\right|-\left|{\mathbf{v}}_{A_i}-{\mathbf{v}}_{B_i}\right|$$

相似度评分的处理

使用相似性评分并不是检测回环的唯一依据。

有些环境的外观本来就很相似，像办公室往往有很多同款式的桌椅；另一些环境则各个地方都有很大的不同。考虑到这种情况，我们会取一个先验相似度 $s(v_t,v_{t-∆t})$，它表示某时刻关键帧图像与上一时刻的关键帧的相似性。然后，其他的分值都参照这个值进行归一化：

$$s{\left({\mathbf{v}}_t,{\mathbf{v}}_{t_j}\right)}^{\prime }=s\left({\mathbf{v}}_t,{\mathbf{v}}_{t_j}\right)/s\left({\mathbf{v}}_t,{\mathbf{v}}_{t-\Delta t}\right)$$

如果当前帧与之前某关键帧的相似度，超过当前帧与上一个关键帧相似度的 3 倍，就认为可能存在回环。这个步骤避免了引入绝对的相似性阈值，使得算法能够适应更多的环境。（为什么3倍，这个步骤好像也避免不了上面那个问题，能理解的同学希望评论区告我，感谢）

关键帧的处理

关键帧不会选的太近，因为选的太近的两个关键帧相似度较高，这样效果不好。从实践上说，用于回环检测的帧最好是稀疏一些，彼此之间不太相同，又能涵盖整个环境。

如果成功检测到了回环，比如说出现在第 1 帧和第 n 帧。那么很可能第n + 1 帧， n + 2 帧都会和第 1 帧构成回环。出现这种情况时，会把“相近”的回环聚成一类，使算法不要反复地检测同一类地回环。

检测之后的验证

词袋的回环检测算法完全依赖于外观而没有利用任何的几何信息，这导致外观相似的图像容易被当成回环。并且，由于词袋不在乎单词顺序，只在意单词有无的表达方式，更容易引发感知偏差（不是回环，但算法检测 是回环）。因此，需要一个验证步骤。
验证方法：

1. 时间一致性检测：设立回环的缓存机制，认为单次检测到的回环并不足以构成良好的约束，而在一段时间中一直检测到的回环，才认为是正确的回环。
2. 空间一致性检测：对回环检测到的两个帧进行特征匹配，估计相机的运动。然后，再把运动放到之前的位姿图中，检查与之前的估计是否有很大的出入。

参考

1.视觉SLAM十四讲