ESKF推导

yoyocry

已于 2022-10-24 11:43:58 修改

阅读量1.5k

点赞数 1

分类专栏： SLAM 卡尔曼滤波文章标签： 1024程序员节

于 2022-10-24 11:32:25 首次发布

本文链接：https://blog.csdn.net/weixin_42040262/article/details/127487605

版权

SLAM 同时被 2 个专栏收录

1 篇文章 0 订阅

订阅专栏

卡尔曼滤波

1 篇文章 0 订阅

订阅专栏

由于高博大佬已经推导得特别好，所以很多地方从高博大佬那粘贴过来。高博大佬的推导链接为：简明ESKF推导 - 知乎 (zhihu.com)

ESKF(error state Kalman filter)是Kalman滤波的一种特殊形式，采用ESKF的原因是由于对误差的线性化要比直接对函数进行线性化更加符合实际情况。如下图：

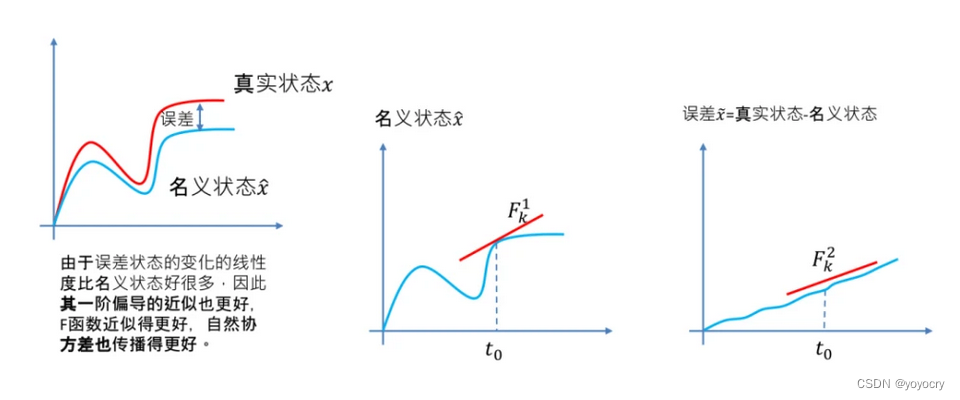在ESKF中，我们通常把包含全部噪声的状态变量称为观测状态变量 $x_{truth}$ 。只有当前正态噪声（无维纳噪声）的变量称为名义状态变量（nominal state） $x$ ，然后把ESKF里的状态变量称为误差状态变量（error state） $\delta x$ 。三者关系为： $x_{truth}=x+\delta x$ 。

1 true state kinematics

对于true state kinematics(动力学), 微分形式有:

$\dot{p}_t=v_t \\ \dot{v}_t=a_t \\ \dot{q}_t=q_{t} \bigotimes \left[ \begin{matrix} 0 \\ \frac{1}{2}w_{t} \end{matrix} \right] \\ \dot{b_{gt}}=\eta_{bg} \\ \dot{b}_{at}=\eta_{ba} \\ \dot{g}_t=0$

对于IMU的真实值 $w_t$ ， $a_t$ 可测量值 $w_m,a_m$ 之间的关系：

$a_m=R_t^{T}(a_t-g_t )+b_{at}+\eta_a \\ w_m=w_t+b_{gt}+\eta_g\\ \Downarrow \\ a_t=R_t(a_m-b_{at}-\eta_a)+g_t \\ w_t=w_m-b_{gt}-\eta_g \\ b_{gt}=b_g+\delta b_g \\ b_{at}=b_a+\delta b_a$

将等式(2)代入等式(1)有：

$\dot{p}_t=v_t \\ \dot{v}_t=R_t(a_m-b_{at}-\eta_a)+g_t \\ \dot{q}_t=\frac{1}{2}q_{t} \bigotimes \left[ \begin{matrix} 0 \\ w_m-b_{gt}-\eta_g \end{matrix} \right] \ or\ \dot{R}_t=R_{t} (w_m-b_{gt}-\eta_g)^{\wedge}\\ \dot{b_{gt}}=\eta_{bg} \\ \dot{b}_{at}=\eta_{ba} \\ \dot{g}_t=0$

注意 $b_{gt}$ 的存在维纳过程的噪声是 $\eta_{bg}$ ， $b_{at}$ 噪声是 $\eta_{ba}$ 。所以存在当前时刻测量噪声 $\eta_{g}$ 和 $\eta_{a}$ ，以及维纳过程中的噪声。

2 Nominal-state kinematics

无时间累计噪声或扰动(无维纳噪声)的理想建模系统，nominal-state中不包含时间累计噪声，从上面公式中去除时间累计Noise项。

$\dot{p}=v \\ \dot{v}=R(a_m-\eta_a)+g \\ \dot{q}=\frac{1}{2}q \bigotimes \left[ \begin{matrix} 0 \\ w_m-\eta_g \end{matrix} \right] \ or\ \dot{R}=R(w_m-\eta_g)^{\wedge}\\ \dot{b_{g}}=0\\ \dot{b}_{a}=0\\ \dot{g}_t=0$

其中加速度和角速度为：

$a=a_m-\eta_a \\ w=w_m-\eta_g$

3 error-state kinematics

将true-state部分的kinematics方程中减去nominal-state就可以得到error-state的kinematics方程。首先定义误差状态变量为:

$p_t=p+\delta p \\ v_t=v+ \delta v\\ q_t=q \bigotimes \delta q \ or\ R_t=R \delta R\\ b_{gt}=b_g+\delta b_g \\ b_{at}=b_a+\delta b_a\\ g_t=g+\delta g \\ \delta q=e^{\frac{1}{2}\delta \theta} \\ \delta R=e^{[\delta \theta]^{\wedge}}$

等式两侧分别对时间求导(注意这里是维纳噪声):

$\dot{\delta p}=\dot{p}_t-\dot{p}=v_t-v=\delta v \\ \dot{\delta b_g}=\dot{b_{gt}}-\dot{b_g}=\eta_{bg}-0=\eta_{bg} \\ \dot{\delta b_a}=\dot{b_{at}}-\dot{b_a}=\eta_{ba}-0=\eta_{ba} \\ \dot{\delta g}_t=\dot{g_{t}}-\dot{g}=0-0=0$

（1）旋转项求导

对于旋转项两侧求导为：

$\dot{q_t}=\dot{\{q \bigotimes \delta q}\}\\ \dot{q}\bigotimes \delta q +q\bigotimes \dot{\delta q }=\dot{q_t}=q_{t} \bigotimes \left[ \begin{matrix} 0 \\ \frac{1}{2}w_{t} \end{matrix} \right] \\ q\bigotimes \left[ \begin{matrix} 0 \\ \frac{1}{2}w\end{matrix} \right] \bigotimes\delta q+q\bigotimes \dot{\delta q }=q \bigotimes \delta q \bigotimes \left[ \begin{matrix} 0 \\ \frac{1}{2}w_{t} \end{matrix} \right]$

两边同乘 $q^{-1}$ 可得：

$\dot{\delta q }= \delta q \bigotimes \left[ \begin{matrix} 0 \\ \frac{1}{2}w_{t} \end{matrix} \right] -\left[ \begin{matrix} 0 \\ \frac{1}{2}w\end{matrix} \right] \bigotimes\delta q \\ 2\dot{\delta q }=[q]_R(w_t) \delta q-[q]_L(w) \delta q \\ =\left[ \begin{matrix} 0 &-(w_t-w) \\ (w_t-w)&-[w_t+w]^{\wedge}\end{matrix} \right]\left[ \begin{matrix} 1 \\ \frac{1}{2}\delta \theta\end{matrix} \right]+O(||\delta \theta||^2) \\ =\left[ \begin{matrix} 0 &-\delta w \\ \delta w&-[w_t+w]^{\wedge}\end{matrix} \right]\left[ \begin{matrix} 1 \\ \frac{1}{2}\delta \theta\end{matrix} \right]+O(||\delta \theta||^2) \\ =\left[ \begin{matrix} 0 &-\delta w \\ \delta w&-[w_t-w+2w]^{\wedge}\end{matrix} \right]\left[ \begin{matrix} 1 \\ \frac{1}{2}\delta \theta\end{matrix} \right]+O(||\delta \theta||^2) \\ =\left[ \begin{matrix} 0 &-\delta w \\ \delta w&(-[ \delta w]-[2w])^{\wedge}\end{matrix} \right]\left[ \begin{matrix} 1 \\ \frac{1}{2}\delta \theta\end{matrix} \right]+O(||\delta \theta||^2)$

注意第三行 $\delta q$ 因为为小量，实部接近于1，虚部近似为角度。注意 $\dot{\delta q }=\left[ \begin{matrix} 1 \\ \frac{1}{2} \dot{\delta \theta }\end{matrix} \right]$ 。所以只需要取虚部即可：

$\dot{\delta \theta }=\delta w-[w]^{\wedge}\delta \theta -\frac{1}{2}[\delta w]^{\wedge}\delta \theta \\ =\delta w-[w]^{\wedge}\delta \theta$

第二行忽略了第一行的第三项的两个小量相乘法。并且，注意 $w_t=w+\delta w$ 。

$w_t=w_m-b_{gt}-\eta_g$ ，将 $b_{gt}=b_g+\delta b_g$ 代入有 $w_t=w_m-b_g-\delta b_g-\eta_g$ 。于是有： $\delta w=-\delta b_g-\eta_g$ 。将这些代入等式（14）有：

$\dot{\delta \theta }=\delta w-[w]^{\wedge}\delta \theta \\ \dot{\delta \theta }=-[w_m-b_g]^{\wedge}\delta \theta-\delta b_g-\eta_g$

（2）速度项推导

$\dot{v_t}=\dot{\{v+ \delta v}\} \\ \dot{v}+\dot{\delta v}=R_t(a_m-b_{at}-\eta_a)+g_t \\ \dot{v}+\dot{\delta v}=R \delta R(a_m-b_{at}-\eta_a)+g+\delta g \\ \dot{v}+\dot{\delta v}=R(I+[\delta \theta]^{\wedge})(a_m-b_a-\delta b_a-\eta_a)+g+\delta g \\ \dot{v}+\dot{\delta v}=(R(a_m-b_a)+g)-R(\delta b_a+\eta_a)+R[\delta \theta]^{\wedge}(a_m-b_a-\delta b_a-\eta_a)$

注意：1） $[\delta \theta]^{\wedge}$ 与 $\delta b_a$ 和 $\eta_a$ 乘法项全为0；2） $\dot{v}=R(a_m-b_a)+g$

所以：

$\dot{\delta v}=-R(\delta b_a+\eta_a)+R[\delta \theta]^{\wedge}(a_m-b_a) \\ \dot{\delta v}=-R(\delta b_a+\eta_a)-R(a_m-b_a)^{\wedge}\delta \theta$

4 离散时间系统运动学

（1）error-state的预测步推导

除了 $p$ ，其余按照 $x(t+\Delta t)=x(t)+\dot{\delta x}\Delta t$ 来计算

nominal state kinematics的离散运动模型

$p(t+\Delta t)=p(t)+v(t)\Delta t+\frac{1}{2}(R(a_m-\eta_a)+g) \Delta t^2 \\ v(t+\Delta t)=v(t)+(R(a_m-\eta_a)+g) \Delta t \\ b_g(t+\Delta t)=b_g(t)=\eta_g \\ b_a(t+\Delta t)=b_a(t)=\eta_a \\ g(t+\Delta t)=g(t) \\ q(t+\Delta t)=q\bigotimes \left[ \begin{matrix} 0 \\ \frac{1}{2}(w_m-\eta_g)\Delta t \end{matrix} \right] or\\ R(t+\Delta t)=R(t)+R(t)(w_m-\eta_g)^{\wedge}\Delta t=R(t)(I+(w_m-\eta_g)^{\wedge}\Delta t) \\ =R(t)exp((w_m-\eta_g)^{\wedge}\Delta t)$

error-state kinematics的离散运动模型

$\delta p(t+\Delta t)=\delta p+\delta v\Delta t \\ \delta v(t+\Delta t)=\delta v+(-R(\delta b_a+\eta_a)-R(a_m-b_a)^{\wedge}\delta \theta)\Delta t \\ \delta \theta(t+\Delta t)=\delta \theta+(-[w_m-b_g]^{\wedge}\delta \theta-\delta b_g-\eta_g)\Delta t \\ \delta b_g(t+\Delta t)=\delta b_g+\eta_{bg} \Delta t \\ \delta b_a(t+\Delta t)=\delta b_a+\eta_{ba} \Delta t \\ \delta g(t+\Delta t)=\delta g$

对第二行和第三行进行展开（第三行中使用泰勒展开）：

$\delta \theta(t+\Delta t)=\delta \theta+(-[w_m-b_g]^{\wedge}\delta \theta-\delta b_g-\eta_g)\Delta t \\=(I+(-[w_m-b_g]^{\wedge}\Delta t))\delta \theta-\Delta t\delta b_g-\eta_g\Delta t \\=exp(-[w_m-b_g]^{\wedge}\Delta t)\delta \theta-\Delta t\delta b_g-\eta_g\Delta t$

结果为：

$\delta p(t+\Delta t)=\delta p+\delta v\Delta t \\ \delta v(t+\Delta t)=\delta v-R(a_m-b_a)^{\wedge}\Delta t\delta \theta-R\Delta t\delta b_a +\eta_a\Delta t\\ \delta \theta(t+\Delta t)=exp(-[w_m-b_g]^{\wedge}\Delta t)\delta \theta-\Delta t\delta b_g-\eta_g\Delta t \\ \delta b_g(t+\Delta t)=\delta b_g+\eta_{bg} \Delta t \\ \delta b_a(t+\Delta t)=\delta b_a+\eta_{ba} \Delta t \\ \delta g(t+\Delta t)=\delta g$

故设状态方程如下：

$\mathbf{x}= \left[ \begin{matrix} p \\v \\\theta \\b_g \\b_a \\g \end{matrix} \right] ,\mathbf{\delta x}=\left[ \begin{matrix} \delta p \\\delta v \\\delta \theta \\\delta b_g \\\delta b_a \\\delta g \end{matrix} \right] ,\mathbf{\mu}= \left[ \begin{matrix} a_m \\w_m \end{matrix} \right] ,\mathbf{i}=\left[ \begin{matrix} p_i\\v_i \\\theta _i \\w_i \\ a _i \\g_i \end{matrix} \right]$

其中 $\mathbf{x},\mathbf{\delta x},\mathbf{\mu},\mathbf{i}$ 分别代表norminal state状态变量，error-state状态变量，输入参数和扰动的噪声项，error-state运动方程满足:

$\mathbf{\delta x}(t+\Delta t )=f(\mathbf{x},\mathbf{\delta x},\mathbf{\mu},\mathbf{i})=F_x(\mathbf{x},\mathbf{\mu})*\delta x+F_i*\mathbf{i}$

所以：

1）

$F_x=\frac{\partial f}{\partial \delta x}=\left[ \begin{matrix} I&I\Delta t&0&0&0&0\\0&I&-R(a_m-b_a)^{\wedge}\Delta t&-R \Delta t&0&I\Delta t\\0&0&-[w_m-b_g]^{\wedge}\Delta t&0&- I\Delta t&0\\0&0&0&I&0&0 \\ 0&0&0&0&I&0\\0&0&0&0&0&I\end{matrix} \right]$

2）

$$$F_i=\frac{\partial f}{\partial i}=\left[ \begin{matrix}0&0&0&0&0&0\\0&I&0&0&0&0 \\ 0&0&I&0&0&0\\0&0&0&I&0&0\\0& 0&0&0&I&0 \\0&0&0&0&0&0 \end{matrix} \right]$

ESKF是扩展卡尔曼滤波的推导，所以下面使用的都是扩展卡尔曼滤波

（2）ESKF滤波

ESKF对IMU信息进行预测，其他信息用于校正滤波器，从而观察IMU bias误差和观测误差。纠正包括三个步骤：

使用ESKF对误差状态变量（error state）进行预测和更新
更新的误差状态（error state）修正名义状态变量（nominal state）
重置ESKF

（2.1）预测与更新

1)ESKF的预测过程（预测过程包括对误差状态的预测和协方差传播的预测）：

$\delta x_{pred}=F_x*\delta x \\ P_{pred}=F_xPF_x^T+F_iQ_iF_i^T$

其中 $Q_i$ 为( $P$ 和 $g$ 不存在扰动，所以为0)：

$Q_i=diag(0,Cov(\eta_a),Cov(\eta_g),Cov(\eta_{bg}),Cov(\eta_{ba}),0)=\left[ \begin{matrix}0&0&0&0&0&0\\0&V_i&0&0&0&0 \\ 0&0&\Theta_i&0&0&0\\0&0&0&\Omega_i&0&0\\0& 0&0&0&A_i&0 \\0&0&0&0&0&0 \end{matrix} \right]$

$\sigma(\boldsymbol{\eta}_a)= \Delta t \sigma \eta_a, \quad \sigma(\boldsymbol{\eta}_{g}) = \Delta t \sigma \eta_{g}, \quad \sigma(\boldsymbol{\eta}_{bg}) = \sqrt{\Delta t} \sigma \eta_{bg}, \quad \sigma(\boldsymbol{\eta}_{ba}) = \sqrt{\Delta t} \sigma \eta_{ba}$

（这里不理解为啥方差是这样子？）

噪声项为：

$P_i=0\\V_i =\sigma^2 \eta_a\Delta^2 tI\\\Theta _i=\sigma^2 \eta_g\Delta^2 tI \\ \Omega _i=\sigma^2 \eta_{bg}\Delta tI \\ A_i=\sigma^2 \eta_{ba}\Delta tI \\G_i=0$

此外，需要使用nominal state kinematics的离散运动模型来估计名义状态的预测 $x$ （IMU积分）

2)ESKF的更新过程：

假设一个抽象的传感器能够对状态变量产生观测（IMU以外的传感器观测），其观测方程为抽象的 $h$ ，则：

$\boldsymbol{z}=h(\boldsymbol{x})+\boldsymbol{v}\sim N(0,V)$

其中 $z$ 为观测数据（其他传感器对x的观测数据）， $v$ 为观测噪声， $V$ 为该噪声的协方差矩阵。

在传统EKF中，我们可以直观对观测方程线性化，求出观测方程相对于状态变量的雅可比矩阵，进而更新卡尔曼滤波器。而在ESKF中，我们当前拥有名义状态（nominal state） $x$ 的估计，以及误差状态 $\delta x_{pred}$ 的估计。

所以算误差状态的更新过程：

$K=P_{pred}H^T(HP_{pred}H^T+V)^{-1} \\ \delta x=K(z-h(\boldsymbol{x_t})) \\ P=(I-KH)P_{pred}$

其中 $\boldsymbol{P}$ 为修正后的协方差矩阵， $\boldsymbol{H}$ 是观测方程相比于误差状态的雅可比矩阵，计算方式如下：

$\boldsymbol{H}=\frac{\partial h}{\partial \boldsymbol{x}}\frac{\partial\boldsymbol{x} }{\partial \delta\boldsymbol{x}}$

其中第一项只需对观测方程进行线性化，第二项根据我们之前对状态变量的定义（见下方），可以得到：

$\frac{\partial \boldsymbol{x}}{\partial \delta \boldsymbol{x}} = \mathrm{diag}(\boldsymbol{I}_3, \boldsymbol{I}_3, \frac{\partial \mathrm{Log} (\boldsymbol{R}(\mathrm{Exp}(\delta \boldsymbol{\theta})))}{\partial \delta \boldsymbol{\theta}}, \boldsymbol{I}_3, \boldsymbol{I}_3, \boldsymbol{I}_3)$

其他几种都是平凡的，只有旋转部分，因为 $\delta\boldsymbol{\theta}$ 定义为 $\boldsymbol{R}$ 的右乘，我们用右乘的BCH近似为：

$\frac{\partial \mathrm{Log} (\boldsymbol{R}(\mathrm{Exp}(\delta \boldsymbol{\theta})))}{\partial \delta \boldsymbol{\theta}} = \boldsymbol{J}_r^{-1} (\boldsymbol{R})$

（2.2）修正nominal state

$p_{k+1}=p_k+\delta p \\ v_{k+1}=v_k+ \delta v\\ q_{k+1}=q_k \bigotimes \delta q_k \ or\ R_{k+1}=R_k \delta R_k\\ b_{g,k+1}=b_{g,k}+\delta b_{g,k} \\ b_{a,k+1}=b_{a,k}+\delta b_{a,k}\\ g_{k+1}=g_k+\delta g \\$