【机器人学中的状态估计】第一讲

1. 什么是状态估计？

通过获得传感器的观测值，建立观测值到状态量的模型，估计出状态量。

2. 概率密度函数

【后验概率】$p(x|y)$为在某观测值$y$下的状态$x$的PDF
【似然】$p(y|x)$为传感器模型，也就是在不同的状态$x$下的观测值$y$的PDF
【先验概率】$p(x)$为状态$x$本身的PDF
$p(y)$是传感器观测值本身的PDF，一般很难直接计算

$p(x)$若看做是均匀分布，也就说在某次观测中，不考虑观测值，直接去猜测状态量，那么所有状态量出现的可能性都是一样多的。但在实践中，某次观测的状态量往往与上次的状态量相关，因此$p(x)$并不是均匀分布的。

独立与相关

所谓不相关就是不线性相关。

归一化积

香农信息与互信息

3. 高斯概率密度函数

协方差矩阵为对称正定矩阵，但是估计出来的协方差不能保证正定性

注意到，在一维高斯分布中，取某条等概率线，它将穿过概率曲线的两个点，这两个点以均值所在竖直线为中心线，并且据该条中心线距离都为$\sigma$。也就说$\sigma$决定了等概率线上的点距均值的距离。

同理，在多维高斯分布的情况下，取等概率面，我们将得到一个椭圆，协方差矩阵$\Sigma$决定了椭圆上的点与椭圆的距离，即椭圆的形状。在各个随机变量的边缘分布的方差都相等的情况下，椭圆退化为圆。

一维高斯分布中全概率公式证明：

（摘自陈希孺《概率论与数理统计》）


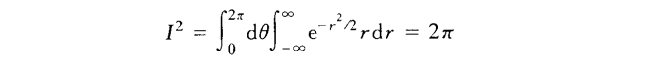
在最后一步极坐标换元操作中，需要对原积分公式的３处进行替换：（１）被积分的表达式，这个是显然的；（２）积分上下界；（３）$dtdu$替换为$rdrd\theta$。

第（３）步值得说道一下。
直接地，分别求出

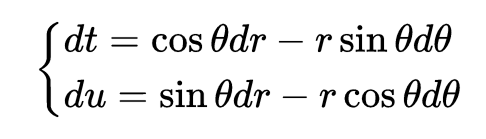
再将它们直接相乘会得到错误的结果，原因是$dt$、$du$等符号比较特殊，不能看做单纯的变量，再深入问为什么我也不知道了。

因此，一般会采用雅克比矩阵来进行换元，暂且记住它吧。

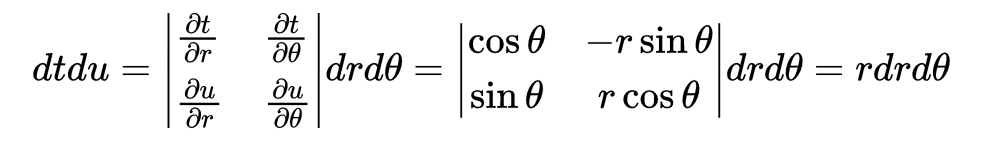
高斯推断/边缘化-联合高斯分布

我们希望利用前面所说的贝叶斯公式：

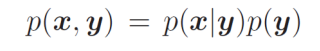
在已知联合分布和边缘分布的情况下推导出条件分布。我们需要求出条件分布的均值和协方差矩阵。这就要求我们把$p(x,y)$的协方差矩阵的逆拆成块状，以便于我们把它的随机变量中的$x$部分和$y$部分分离出来。下面会进行详细解释。

分块矩阵打洞：

第一种方式：

其中，$D-C{A}^{-1}B$叫做$A$的舒尔补（Schur Complement）。

第二种方式：



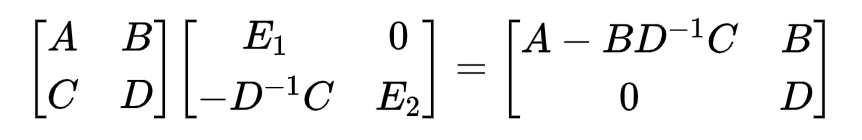
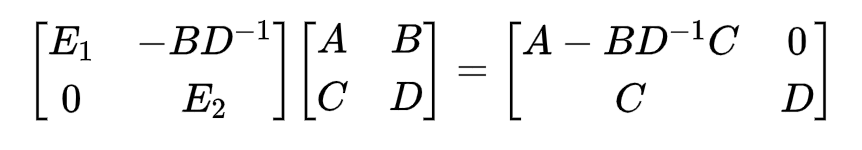
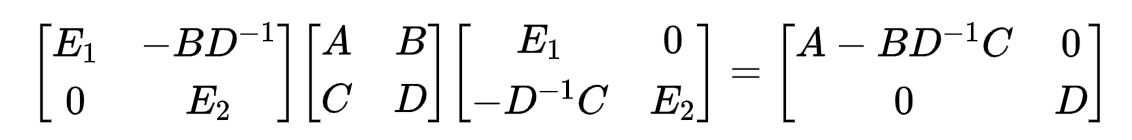
其中，$A-B{D}^{-1}C$叫做$D$的舒尔补（Schur Complement）。

进一步地，为了呈现课程PPT中的形式，把第二种方式左侧两个操作矩阵取逆放到右侧，有

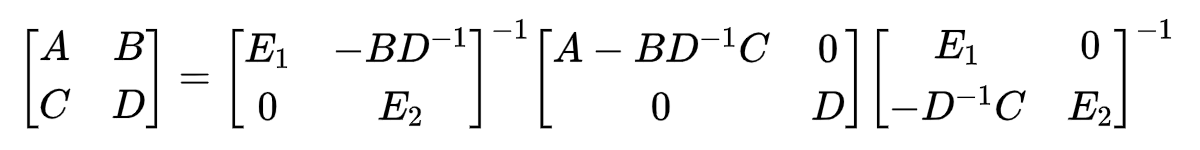
再把公式左右两侧都取逆，有

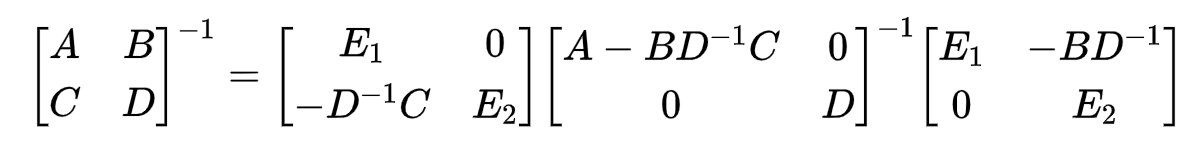
把上述示例矩阵替换为协方差矩阵，就可以得到以下的形式：

这么做的目的是，为了可以把大的联合的协方差的矩阵的求逆转换为一个新矩阵内部的分块的求逆，便于代入高斯密度函数中的二次型，即$(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )$，如下：

上述的二次型同时包含了期望和协方差信息，也就是高斯分布的全部信息了。

我们上面了做了这么多工作的目的是进行边缘化，也就是把条件概率密度函数从联合概率密度函数中分离出来，依据以下公式：
$$p(x,y)=p(x|y)p(y)$$
由于二次型包含了高斯分布的全部信息，因此我们只需要在二次型中把$p(x|y)$和$p(y)$的期望和协方差分离出来就行。借助上面的矩阵打洞，我们把$p(x,y)$的协方差的逆顺利拆散了，并进行分离。

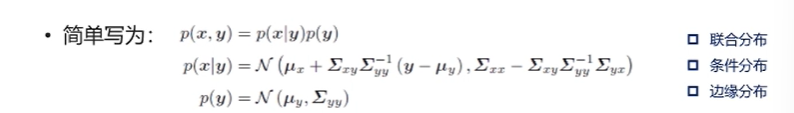
高斯分布的变换

（1）线性变换


线性变换前，随机变量服从高斯分布，则线性变换后仍然服从线性变换。

（2）非线性变换
非线性变换的情况下，得到的$p(x)$不服从高斯分布。

举个标量的例子：

我觉得这里的推导比较玄学…
线性化

一维情况下的例子：

下面的推导非常难，反正我没看懂：

高斯分布的不相关性等价于独立性

归一化积

4个SMW恒等式

其实仍然是矩阵填洞，只是把两种不同的填洞方法给等价起来。


（1+3个相乘）的逆
（1+3个相乘）的逆再乘（2个相乘）