HDNet: Hybrid Distance Network for semantic segmentation

摘要

语义分割是一种基于像素的标注任务，即根据每个像素的特征预测每个像素的标签。然而，现有的方法分离了特征图中点之间的关系，导致分割结果不连续。为了解决这一问题，我们提出了一种混合距离网络HDNet来从两个方面来测量距离。

首先，本文提出一种混合距离关系模型来对某点与其上下文区域之间的关系进行建模，即结合位置距离和高维特征距离来捕获特征图中的上下文contexts。在此基础上，本文提出了位置感知注意模块，通过位置距离对上下文进行有效采样，并产生稀疏混合距离关系 Hybrid Distance Relations。它综合了每个点的不同上下文，并根据位置生成注意值来压缩对象级表示。在训练过程中，高维特征距离损失也作为一种辅助损失来拉近相同类别间在特征空间中的表示。

实验表明，在Pascal Context、ADE20K和COCO Stuff 10k三个具有挑战性的语义分割基准上，本文提出的HDNet在可解释性和效率方面都达到了最先进的性能。

Introduction

语义分割是计算机视觉的一项基本任务，它预测输入图像的每个像素的语义类别。它将分类与定位相结合，广泛应用于计算机辅助诊断[1]、自动驾驶[2]、场景理解[3]、图像编辑[4]等领域。自从全卷积网络FCN[5]首次将卷积神经网络引入密集预测任务以来，语义分割问题就在用端到端深度神经网络来解决问题。CNN主要采用$3\times 3$大小的滑动窗口来进行卷积运算，这样既可以让每个点都具有一定的感受域，又能让计算负担在可承受范围内。但是ACNet[6]证明了卷积核主要集中在中心点上，所以滑动窗口的过程会造成每个点的割裂。这种割裂会干扰特征学习，导致分割结果的不连续，这种情况称为“割裂问题”。此外，大多数语义分割网络使用像素级交叉熵作为criterion[5,7,8]，其中相邻点也是被孤立监督的。该criterion不能有效地惩罚不连续的分割结果，因此加重了分割的“割裂问题”。

为了解决割裂问题，许多模块致力于捕捉每个点的上下文信息。DeepLab v1[7]设计了atrous卷积来扩大感受域。但是这一策略仍会造成点与全局场景上下文的割裂。金字塔模块(Pyramid Pool Module, PPM)[8]充分利用了池化层的聚合效果，可以得到不同窗口大小下的合成表示，如图1a所示。然而，池化操作产生聚合的特征，却丢失了每个池化窗口中的所有空间信息。当两个点位于同一个池化窗口时，它们会获得相同但不准确的上下文信息。而且，位于两个池化窗口中的两个相邻点将获得完全不同的上下文。

近年来，Non-Local[10]模块通过对高维特征空间中的点的成对关系进行建模，来获取远距离的上下文信息，如图1b所示。但是它使用同样的策略来生成对空间所有位置的注意力，在这些空间位置中，长距和短距的contexts发挥着同样的作用。这种关系表示忽略了点对之间的位置距离的影响，也丢失了对象的整体概念。因此，它不能解决对象内部的割裂问题，还会导致大量的冗余计算。实际上，每个点都有与其位置相关的上下文信息，但上述方法在获取上下文信息时丢弃了空间信息，造成了分割精度的降低。

为了解决割裂问题，并利用相对位置[11]的优势，本文首先提出一种混合距离关系(HDR)，HDR可以通过位置距离和高维特征距离的巧妙结合来获取每个点自身的上下文信息。位置距离表示特征图中一对点之间的相对位置，高维特征距离表示两个特征向量之间的相似度。我们的HDR在一定范围内对点与其上下文区域之间的关系进行建模，其中位置距离隐含在该区域的范围内。其次，我们采用位置感知注意力(Location Aware Attention, LAA)模块对不同位置距离的HDR进行采样，从而获取点与其不同上下文之间的关系，如图1c所示。

然后由这些HDR生成一个基于位置的注意力值，以此融合不同的关系，并补充原有的特征图。LAA模块引入稀疏关系连接来关注高维空间中特征的位置距离，这比以往的方法使用每对之间的密集连接减少了计算复杂度[12,13]。它感知中心位置周围物体的空间关系，以较低的计算复杂度增强分割结果的连续性。利用这一特性，我们的方法在对象中的特征分布比Non-Local based方法更紧凑，如图2所示，其中不同对象在图2d中更有区别，特别是小对象。

一个样本图像和可视化特征。(a) (b)是图像和相应的真实结果。© (d)是经过Non-Local模块和我们的LAA模块后的可视化特征图，其中特征维数由512降为3。

最后，我们设计了一个辅助损失来缩小高维空间中同类之间的特征距离，放大不同类别间的特征距离。混合距离网络(HDNet)在三个数据集上的实验表明了该方法的有效性和可解释性。

本文主要贡献如下:

• 该算法结合高维特征距离和位置距离，对每个点与其不同上下文之间的关系进行建模，从而获得点的上下文信息。

• 我们提出了LAA模块来采样HDR的位置距离，并感知每个点的不同上下文，从而增强了特征的对象级连续性。

• 我们设计了高维特征距离损失(HFD)，通过寻找每个类别的特征中心来监督类别级的特征连续性。

• 我们提出的HDNet在三个具有挑战性的数据集上实现了最先进的性能，包括ADE20K[14]、PASCAL Context[15]和COCO Stuff 10k[16]。

Related work

Approach

在这一节中，我们将介绍如图3所示的HDNet。

首先，我们提出了一种结合高维特征距离和位置距离的HDR建模策略来对点与其上下文区域之间的关系进行建模。

其次，我们提出一个LAA模块(图3中的蓝色块)对不同的位置距离进行采样，产生稀疏连接。每个点都可以通过LAA感知对象的位置，并通过位置注意力进一步增强对象层面的连续性。由于LAA作为空间注意模块可以沿空间维度增强feature map，因此DANet[12]中在CAM模块之后还有一个平行通道注意。

将这两个残差注意力特征融合到原始的feature map中，可以从空间和通道两个方面进行正交增强。因此，feature map中的每个feature都可以重新缩放。

最后，我们设计一个HFD loss(图3中的红色块)来求每个类别的特征中心，通过高维空间中的特征距离提高类别级的连续性。

1.Hybrid Distance Relation

神经网络解决分割任务的孤立方式使最终结果不连续。目前的方法只关注上下文信息的捕获，而不考虑特征的连续性，不能很好地解决割裂问题。为了产生连续的结果，避免计算冗余的成对连接，我们提出HDR来建模点与其不同上下文之间的关系，它可以迫使每个点在不同的范围感知其周围的区域。HDR基于上下文区域的中心点和聚集特征，可表示为：

$$R_k(i,j)=\mathcal{F}(X_{ij},{\mathcal{A}}_k(X_{ij}))$$

式中$X_{ij}$为某点在坐标 $(i,j)$处的特征向量； $k$表示位置范围，${\mathcal{A}}_k(X_{ij})$聚合由中心点$X_{ij}$和范围$k$指定的上下文区域的特征。${\mathcal{A}}_k(X_{ij})$产生的特征和$X_{ij}$的维度相同。$\mathcal{F}(,)$是计算两个给定向量之间高维特征距离的测量函数。$R_k(i,j)$表示$X_{ij}$和以$X_{ij}$为中心范围$k$内的上下文区域的关系。通过$k$的设置，HDR可以对短距和长距关系进行建模。

HDR的本质是两个特征向量之间的特征距离，并且每个HDR通过聚合函数${\mathcal{A}}_k(.)$使用采样的特征图来让点感知它周围的区域。位置距离指的是周围区域的范围，所以位置距离的影响通过聚合函数${\mathcal{A}}_k(.)$嵌入到关系中，而且HDR同时考虑了高维特征距离和位置距离。

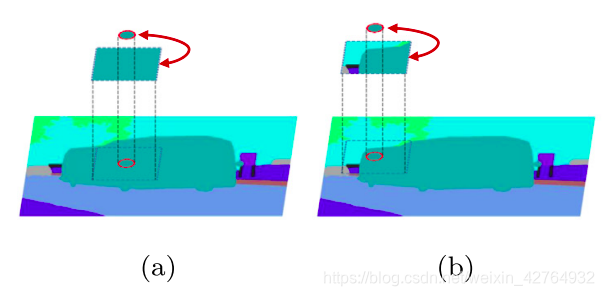
为了明确，当周围区域覆盖与中心点相同的对象时(图4a)， HDR代表对象内上下文信息，其中特征应该趋于一致。相反，HDR包含对象间和对象内上下文信息，如图4b所示。考虑k的多次选择，如果中心点位于一个大的物体上(图4c)，产生的不同范围的关系都在单个物体内，相对产生高响应。相反，中心点一旦位于小对象或边界附近，则只有短程关系表示该对象中的上下文，而k较大时会产生对象间的关系，如图4d所示。

通过逐渐扩大范围k，当应用多个hdr时，中心点可以意识到自己的目标位置。也就是说，由于k的范围不同，中心点可以感知到二维平面中物体边界的空间距离。

此外，我们所提出的HDRs在捕获不同k范围的中心点与其上下文区域之间的关系时可以被可视化为稀疏连接(图5b)，而不是使用孤立点对之间的密集连接(图5a)。

如果HDRs同时关注 $k_n$ 和 $k_{n-1}$ 区间(n为不同k值的索引)，则这两个关系的不同代表了区间 $k_n$ 和 $k_{n-1}$ 之间的上下文关系，如图5c所示，使得上下文信息多样化。虽然单个HDR只涉及到一个规则形状的区域，但多孔区域用更少且到中心的位置距离更具体的点 丰富了关系表示。

在实际应用中，HDR的距离测量函数$\mathcal{F}(,)$可以简单地实现为$\mathcal{F}\left({\mathbf{x}}_{i,j},{\mathcal{A}}_k\left({\mathbf{x}}_{i,j}\right)\right)=\frac{{\mathbf{x}}_{i,j}^T{\mathcal{A}}_k\left({\mathbf{x}}_{i,j}\right)}{\Vert {\mathbf{x}}_{i,j}\Vert \Vert {\mathcal{A}}_k\left({\mathbf{x}}_{i,j}\right)\Vert }$通过标准化因子$\Vert {\mathbf{x}}_{i,j}\Vert \Vert {\mathcal{A}}_k\left({\mathbf{x}}_{i,j}\right)\Vert$该关系主要关注点的特征分布，而忽略了其特征值的大小。此外，归一化还将关系值限制为[0,1]，有利于后续操作。为了简化聚合过程的计算，我们使用池化操作作为聚合函数${\mathcal{A}}_k(.)$，其中范围k被专门化为池化窗口的大小。因此，一个特定距离内的区域是一个正方形。${\mathcal{A}}_k(.)$采用平均池化操作，考虑k范围内的所有点，在一个大对象中，无论窗口大小如何，都产生一致的响应。此外，我们还采用了最大池化操作，可以捕获显著特征。为了使每个点获得自己的聚合结果，将聚合函数设为一个position-wise函数，步幅设为1。由于k的值不同，从局部的角度来看，这一系列聚合函数$\left({\mathcal{A}}_{k_1}(\cdot ),{\mathcal{A}}_{k_2}(\cdot ),\dots ,{\mathcal{A}}_{k_n}(\cdot )\right)$可以看作是一个position-wise的金字塔池化操作。

(a)是原始的feature map，下面是PPM生成的聚合结果。feature map被分别降采样为11,22,33,66个大小。在每个特征图中有两个相邻的点，分别用蓝色和橙色表示。

尽管这种基于位置的聚合和普通PPM[8]都是针对不同上下文的多尺度聚合，但不同的动机会导致不同的结构和结果。具体来说，PPM模块是特性映射的全局金字塔，它强制池结果保持固定的小尺寸。通过这种降采样策略，相邻点可以得到相同或不同的上下文信息，如图6所示。蓝色和橙色突出显示的相邻点被划分为不同的池化窗口，从而获得不同的上下文信息。这种全局方式将丢弃特定的位置，这只会产生不精确的上下文信息。但是，基于位置的聚合$\left({\mathcal{A}}_{k_1}(\cdot ),{\mathcal{A}}_{k_2}(\cdot ),\dots ,{\mathcal{A}}_{k_n}(\cdot )\right)$是每个点的局部金字塔，所以feature map中有H*W (feature map的高度和宽度)金字塔，其中每个点都有自己的上下文。HDRs的可视化聚合结果如图7所示，随着范围k的增大，模糊区域从边界向内部物体扩展。

位置感知注意模块LAA的详细信息。箭头的颜色代表不同类型的特征。黑色箭头表示原始特征，包括下采样特征。蓝色箭头表示聚合的特性。橙色箭头表示关系或位置相关的注意值

ASPP[17]是另一个捕获上下文信息的位置金字塔，因此它可以与hdr中提议的聚合相同。但它继承了扩张性卷积的缺点，即只采样感受野中的少数点，而看不到整个感受野。而池化操作可以考虑整个领域，这不会导致这种不连续效应。与ASPP或PPM的变体的比较见表4第4.2.2节。

由于所提出的HDR是高维特征距离和位置距离的结合，表示点与其周围区域之间的稀疏关系，因此比基于Non-Local的关系模型更高效、连续[12,13,21]。

2. Location Aware Attention

LAA模块可以利用HDR捕获不同范围的上下文，增强对象大小的感知，增强对象级的连续性。如图7所示，LAA有4个子模块:输入/输出变换、多尺度HDRs、HDRs结果的交互、对原始特征图的激励。

LAA的变换子模块包含$\theta$和$\phi$运算，如图7所示。具体来说，输入变换$\theta$通过1*1卷积减少了高效计算的通道数，而输出变换$\phi$也是1*1卷积，但输入和输出之间的通道数相同。这些都是LAA模块中必要的操作，详细的设置在第4.1节中描述。

交互子模块遵循hdr，在每个点融合不同的关系，可以表述为:$${\mathbf{u}}_{i,j}=\omega \left(\left[R_{k_1}(i,j),R_{k_2}(i,j),\dots ,R_{k_n}(i,j)\right]\right)$$

其中$k_1,k_2,\dots ,k_n$表示不同的范围，$\omega (\cdot )$是不同关系的位置非线性融合。由于$R_{k_1}(i,j)$的实现，每个关系都被定义为点上的标量值。所以$\omega (\cdot )$的输入有n个通道来表示n个关系，结果${\mathbf{u}}_{i,j}$包含1个通道作为每个位置的激励权值。

接下来，激励子模块根据前一个结果对原始特征地图进行缩放:$${\mathbf{v}}_{i,j}={\mathbf{u}}_{i,j}\times {\mathbf{x}}_{i,j}$$
为了进行空间注意，每个位置只有一个注意值，向量$x_{ij}$中沿通道维度的特征将同时重新缩放。因此，${\mathbf{v}}_{i,j}={\mathbf{u}}_{i,j}\times {\mathbf{x}}_{i,j}$表示注意值乘以原始特征，结果$v_{ij}$是与原始特征$x_{ij}$形状相同的残差补充。

最终结果${\mathbf{y}}_{i,j}$包含两个项:单位映射$x_{ij}$和来自$v_{ij}$的互补上下文，它们可以表述为位置上的增强:$${\mathbf{y}}_{i,j}={\mathbf{x}}_{i,j}+\phi \left({\mathbf{v}}_{i,j}\right)$$

向后传播时，${\mathbf{y}}_{i,j}$的梯度计算为:$$\begin{array}{rl}\frac{\partial {\mathbf{y}}_{i,j}}{\partial {\mathbf{x}}_{i,j}}& =\frac{\partial {\mathbf{x}}_{i,j}}{\partial {\mathbf{x}}_{i,j}}+\frac{\partial \phi \left({\mathbf{v}}_{i,j}\right)}{\partial {\mathbf{x}}_{i,j}}\\ & =1+\phi \left(\frac{\partial {\mathbf{u}}_{i,j}}{\partial {\mathbf{x}}_{i,j}}+{\mathbf{u}}_{i,j}\right)\end{array}$$
由于单位映射，梯度通过前一项有效地传播到${\mathbf{x}}_{i,j}$。LAA捕获的上下文信息通过后一项传播到周围区域。所以梯度保持了${\mathbf{x}}_{i,j}$的误差，同时关注不同的关系。然而，当前主流上下文模型中的向后传播，特别是non - local模块，依赖于feature map中的所有点，带来了更多的噪声。此外，与传统的联合计算这两种距离的方法不同，该模块将位置距离隐含在k范围内，然后通过可学习参数向量$\omega$探索不同位置距离下特征距离之间的潜在关系。

如图3中蓝色块所示，LAA模块遵循backbone网络，具有单位映射和残差注意力路径。它对原特征图进行了补充，增强了对象级的连续性。此外，我们还在后续的同时使用了一个额外的通道注意力模块(图3中的绿色块)。

得益于稀疏关系和位置注意力，我们的注意力模块的计算复杂度明显低于Non-Local方法。首先，通过我们的HDR策略将稠密关系连接简化为稀疏连接。实际上，在我们的实验中，在某一点上只计算了15个关系，而EMANet[21]在最佳情况下是64，而且DANet[12]和CCNet[13]都依赖于大量的输入点。然后，关系交互和激励是position-wise操作，是对每个点原有特征的补充，提示位置感知。

3. High-dimension feature distance loss

目前的网络[12,13,21]使用头部结构减少feature map的通道来对每个点进行分类，这是一种从高维特征到预测语义类别的有效概要，而潜在特征的监督仅依赖梯度通过。为了预测类别内的连续结果和类别间的区分结果，高维特征应保持相同的一致性和差异性。

本文提出HFD损失来减小类别内所有点的特征距离方差，增加类别间的方差。如图8所示，HFD损失是为了使点与相应类别的归一化特征距离的期望负对数似然值最小化，从而使点更接近同类的中心，远离异类中心。$${\mathcal{L}}_{H,p}=-E_{\mathbf{x}}\left[\log \widetilde{D_p}(\mathbf{x})\right]$$
其中x是一个点的特征，$\widetilde{D_p}(\mathbf{x})$为x与ground truth表示的第p个类别特征中心的归一化距离。与无监督聚类方法类似，HFD loss探索每个类别的特征中心，并迫使每个点靠近相应的中心。为了获得点与类别中心之间的精确对应关系，使用ground truth来监督结果，这是与聚类方法的主要区别。

在前向传播过程中，我们通过点到每个特征中心之间的点产生来计算高维特征距离，并用一个softmax函数进行归一化:
$${\tilde{D}}_q(x)=\frac{\exp \left(T_q^{T}x\right)}{{\sum }_n^N\exp \left(T_n^{T}x\right)}$$其中q为类别的索引，N为类别的个数。我们提出了$T\in {\mathbb{R}}^{C\times N}$这样的查询表来存储每个类别的必要特征，像在线实例匹配方法一样，其中C是特征的个数。Tq表示第q个中心，结果${\tilde{D}}_q(x)$表示x点到这个中心的距离。

查找表T是依赖于生成的feature map的每个类别的高维表示。在训练过程中，它会随着feature map的变化而不断更新。但是训练过程的一个步骤是基于一批数据集，其中只包含少量的图像。为了通过小批量逼近真实表示，在更新过程中采用指数移动平均策略，这与批归一化层相同。所以更新不需要梯度，而是依赖于图8中黑色虚线的输入，公式为$$T_q^{(e)}\leftarrow (1-d(\gamma ))T_q^{(e-1)}+d(\gamma )\left(\frac{1}{n}\sum x_{i,j}\right),whereG{T}_{i,j}=q$$

e为迭代次数，$\gamma$为初始更新权值。为了加快收敛速度，对$\gamma$同时采用了衰减策略$d(\gamma )$。$x_{ij}$为坐标(i,j)点处的特征，n为点的总数。对于一个特征中心Tq，只考虑相应的点，其中每个点的ground truth中的类别都等于q。

图9显示了训练过程中各个epoch特征的变化。线条表示平均变化，而面积表示沿特征变化的最大值和最小值。变化在第一个时期迅速减少，并趋于稳定。当将衰减策略d应用于更新权值γ时，变化会变小，特别是在最后一个epoch。

所提出的HFD损失使每个点的高维特征更接近ground truth所表示的相应特征中心Tp，并直接促进了高维特征空间中的类别判别。如图3所示，提出的HFD损失在头部结构之前作为辅助损失监督高维特征图。而传统的交叉熵损失也通过最终的分割结果来监督HDNet。

实验

本节在PASCAL Context[15]、ADE20K[14]和COCO Stuff 10k[16]三个具有挑战性的数据集上进行了综合实验。对所设计模块的各个部分进行了烧蚀实验。。。

1. 实现细节

我们基于PyTorch实现我们的方法。接下来，我们使用ResNet-101和8个下采样作为骨干。在图3中，经过预处理的ResNet (res-5块)之后进行卷积运算，将通道数量从2048减少到512。在LAA模块中，$\theta$操作将通道数量从512个减少到64个，以便进一步有效地提取关系。输出转换$\phi$不改变通道的数量，输出特性映射有512个通道，与单位映射流相同。
图3中的并行通道注意模块紧随DANet[12]中的CAM模块。由于CAM中的通道级亲和矩阵，feature map可以沿通道维度进行增强，这是对我们的LAA模块的正交补充。最后，HFD损失在最后的卷积层之前监督feature map，而一般的交叉熵损失也应用于最终的分割结果。整个损失记为$${\mathcal{L}}_{\text{total }}={\mathcal{L}}_{\mathrm{C}\mathrm{E}}+0.1\times {\mathcal{L}}_{\mathrm{H}}$$

我们以初始学习率0.001乘以KaTeX parse error: Expected '}', got '_' at position 37: …}{\text { total_̲iter }}\right)^…对模型进行80个epoch的训练，HFD loss中的参数γ设置为0.001，衰减策略与学习速率相同。Momentum系数和weight decay系数分别设置为0.9和0.0001。

训练步骤中使用了数据增强，如随机调整大小(范围从0.5到2.0)、随机裁剪(裁剪大小为513)和随机左右翻转.

批大小设置为8。我们采用了平均池法和最大池法，以及具有8个不同窗口大小（1; 3; 5; 7; 9; 11; 15; 19）的LAA模块。
训练过程可以总结为算法1。而在测试阶段[8,9,12]也采用了0.5 ~ 2.2的多尺度测试策略。在训练和推理过程中没有其他技巧。类间相交均值(mIoU)作为评价指标，值越高表示性能越好。

算法小结：
网络初始化

1. 开始循环迭代训练
2. 预处理输入图像和GT
3. 前向传播得到预测结果
4. 提取预测头之前的高维特征
5. 计算预测和GT的交叉熵损失
6. 计算高维距离损失HFD
7. 计算损失之和
8. 反向传播更新参数
9. 更新查询表T