差速轮平滑运动控制

  差速轮机器人由于其简洁的结构、较大的负载、较长的续航时间在仓储物流行业中有较多的应用。其中运动控制作为基础的功能之一是保证安全可靠运行的基础，以李雅普诺夫稳定为依据设计的运动控制器对差速轮机器人运行的平稳性有较好的效果。

运动学模型分析

图1

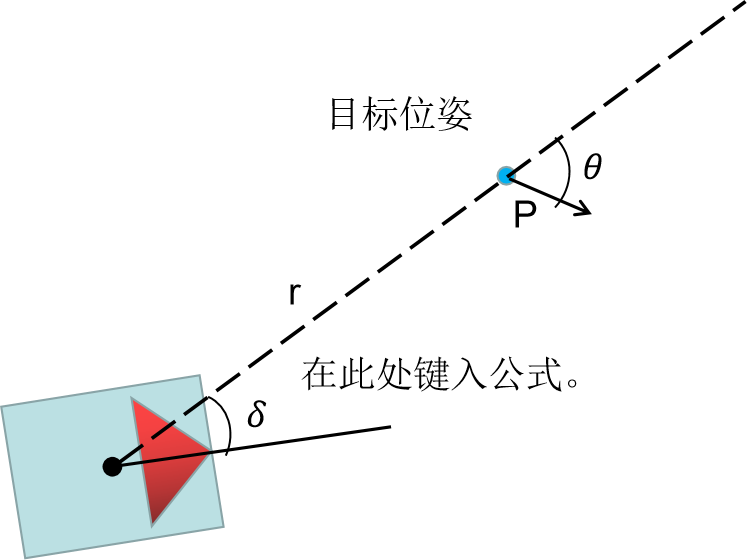
  差速轮机器人的运动学模型如图1所示，$r$ 表示机器人中心距离目标位姿的长度，$\delta$表示机器人方向与$r$所成的角度，$\theta$与$r$所成的角度，其状态方程如下：
$$\begin{array}{l}\dot{r}=-v\cos \delta \\ \dot{\theta }=\frac{v}{r}\sin \delta \\ \dot{\delta }=w+\frac{v}{r}\sin \theta \end{array}\text{\hspace{1em}(1)}$$

  从状态方程（1）中可以看出$r$和$\theta$与线速度$v$相关，因此在通过李雅普诺夫稳定设计控制器时先保证$r$和$\theta$稳定，再设计$w$使得$\delta$稳定。

控制率原理推导

  通过李雅普诺夫稳定性判据可知如果能找到一个正定的由状态变量组成的函数(李雅普诺夫函数)，且函数的一阶导为负定，则系统是渐进稳定的。
  李雅普诺夫函数设计如式（2）所示。
$$V(t)=0.5\ast (r^2+{\theta }^2)\text{\hspace{1em}(2)}$$
  李雅普诺夫函数对时间的一阶导如式（3）所示。
$$\dot{V(t)}=r\dot{r}+\theta \dot{\theta }\text{\hspace{1em}(3)}$$
  令$\delta =\arctan (-k_1\theta )$，$\dot{V(t)}=-rvcos[arctan(-{\mathrm{k}}_1\theta )]+\theta \frac{v}{r}sin[arctan(-{\mathrm{k}}_1\theta )]$，由于$r>0，v>0,-\pi <\delta <\pi ，k_1>0$，所以$-rvcos(arctan(-{\mathrm{k}}_1\theta ))<0$，$\theta \frac{v}{r}sin[arctan(-{\mathrm{k}}_1\theta )]<0$，$\dot{V(t)}<0$，$r，\theta$满足渐进稳定条件。为了保证$\delta$也是渐进稳定的，重新定义一个李雅普诺夫函数，如式（4）所示。
$$Z=\delta -\arctan (-k_1\theta )\text{\hspace{1em}(4)}$$
  令$Z=\delta -\arctan (-k_1\theta )$得式5。
$$\dot{Z}=\dot{\delta }-\frac{k_1}{1+k_1^2{\theta }^2}\dot{\theta }\text{\hspace{1em}(5)}$$
  将式（1）代人式（5）得式（6）。
$$\dot{Z}=w+\frac{v}{r}(1+\frac{k_1}{1+k_1^2{\theta }^2})\delta \text{\hspace{1em}(5)}$$
  令$w=-k_{2}Z-\frac{v}{r}(1+\frac{k_1}{1+k_1^2{\theta }^2})\delta ，k_2>0$，并代人式（5）中得，$\dot{Z}=-k_{2}Z$，因此系统“$Z=\delta -\arctan (-k_1\theta )$”是渐进稳定的，也意味着$\delta$将无线接近$\arctan (-k_1\theta )$，使机器人最终达到目标角度$\theta$。
  因此机器人角速度$w$的控制率为：
$$w=-k_{2}Z-\frac{v}{r}(1+\frac{k_1}{1+k_1^2{\theta }^2})\delta =-k_2(\delta -\arctan (-k_1\theta ))-\frac{v}{r}(1+\frac{k_1}{1+k_1^2{\theta }^2})\delta ，k_1,k_2>0$$

注意事项

1. 参数$k_1，k_2>0$；
2. 在跟踪取消的时候，目标点随着机器人位置发生变化，目标点与机器人的速度相关；
3. 当机器人接近目标点时，存在奇点的情况；