【机器人算法】二连杆机器人动力学参数辨识

本篇博文以二连杆系统为例子，讲解机器人的动力学参数辨识，并进行仿真，由于本篇主要是进行仿真因此没有实验数据处理的过程。

本篇博文主要参考了霍伟的《机器人动力学与控制》。

机器人动力学参数主要步骤：

• 牛顿欧拉动力学建模
• 向外迭代线性化
• 提取最小参数集
• 激励轨迹设计
• 最小二乘法求出动力学参数

动力学建模的方法不用赘述，请参见《机器人学建模、规划与控制》

其中在向外迭代的过程中，对标黄部分进行线性化处理：

于是就可以得到动力学方程的线性化的形式。

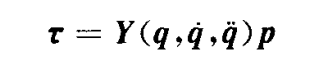
这个时候并不能直接使用最小二乘法，因为Y矩阵不满秩，并且如果使用SVD等方式进行伪逆解处理时，由于Y矩阵的条件数较大，Y矩阵是一个病态矩阵，这就导致伪逆计算的结果十分不精确，并且没有实际的物理意义，比如说将质量计算为负值等等的。因此需要对观测矩阵Y和惯量参数矩阵进行修改。
这就涉及到了最小参数集的提取，最小参数集的提取方法见《霍伟》P97页。
对于二连杆系统，其最小参数集为：

Y矩阵和各个关节的位置、速度和加速度有关。因此激励轨迹将直接影响到Y.'*Y求逆时候的可信度，因此需要优化激