非饱和部分的写作

非饱和带数值模拟方法逐渐成为估计区域地下水补给时空分布的通用方法（ Keese，2005；）；

此类模型主要包括 DAISY、UNSAT-H、SWAP、和HYDRUS -1D，虽然这些模型能够模拟非饱和带中的水流并估算蒸发量和地下水补给量,其应用过程中通常需要指定模型下边界条件(如潜水面位置),没有耦合饱和带地下水流动过程。

因此其结果不能直接反映出气候变化、土地利用和土壤质地对地下水动态的影响。

近年来开发的耦合非饱和带和饱和带水流过程的数值模型,如HYDRUS-3D(Šimůnek,2006),MODFLOW-VSF(Thom等,2006)和HydroGeoSphere(Therrien等,2005),是对上述非饱和带数值模型的巨大改进。

然而，这些模型的理论基础是刻画非饱和带水流过程的理查德(Richards’)方程，其应用主要受到计算机计算能力的限制(van Walsum和Groenendijk,2008)。

而对于流域尺度的模拟计算,将非饱和带内水分运动假设为一维流动通常是合理的(Harter和Hopmans,2004)。因此,许多模型,如MIKE-SHE(Refsgaard等,1995)和MODFLOW-UZF(Niswonger等,2006)采用了非饱和带一维流动和饱和带三维流动的耦合方式以降低耦合模型的复杂程度和提高计算效率。在这些模型中,一维的理查德(Richards’)方程被进一步近似成运动波(kinematic-wave)方程并采用特征值方法求解。该求解方法的优点在于不需要对非饱和带进行网格剖分(Niswonger等,2006)。

基于非饱和带水流过程模拟估算区域地下水补给量的主要困难在于模型参数的获取和尺度转化,如土壤的渗透系数。对于该过程,Harter和Hopman(s2004) 对多种地质统计方法提升土壤渗透系数的空间尺度做了细致的综述性讨论,但这些方法是基于大量的小尺度范围内的渗透系数估算结果(Vereecken等,2007)。

作为直接测量原状土壤渗透系数的替换方法,土壤转换函数方法(PTFs)(Wösten,2001)能有效的用于区域非饱和带渗透系数的估算。利用土壤转换函数方法可以直接测量土壤特征指标(通常附带于土壤调查数据库)并估算非饱和的水力参数(Li等,2007)。许多广泛应用的土壤转换函数方法是基于统计模型的方法(Pachepsky和Rawls,2004)估算土壤水特征函数和饱和渗透系数。所利用的土壤特征指标通常为土壤颗粒分级,土壤干密度和有机成分含量(Nemes等,2003)。 

绝大多数非饱和带数值模拟软件最初的开发目的是用于农业领域研究工作,需要大量反应植被生长特征的参数。虽然土地利用和植被类型分布可以通过调查统计直接获得,遥感解译也有助于获取植被参数,但对于植被类型和土地利用不是地下水补给主控因素的地区,简化植被生长过程模拟,减少模型参数更有利于减少模型的不确定性和模型校正过程中的不唯一性。 蒸散发(ET),作为土壤水均衡的主要排泄项,对利用包气带数值模拟方法计算地下水补给有着重要影响(环境同位素方法估计地下水补给不需要蒸散发的计算)。上述不同的模型中对蒸散发的计算过程也各不相同。最常用的计算方式首先是基于常规气象观测数据计算潜在蒸发或参考蒸散发(ETp或ET0)(Lu等,2005),然后利用经验公式计算裸土蒸发和植物蒸腾(如Šimůnek等,2005)。实际蒸发和植物蒸腾根据土壤含水量情况和植被信息确定,并加和得到实际蒸散发(ETa)。但是,这种方法通常要求较小的时间尺度,如日气象数据。因此,饱和带水流模型的时间步长也需要相应减小,但对于饱和带地下水流、特别是大区域地下水流模型来说,显然是不合适的。作为一种折衷方案,可以利用子时间步长,即在饱和带水流模型时间步长的基础上再进行剖分,得到的更小时间步长作为非饱和带模型的时间步长,如耦合HYDRUS和MODFLOW的程序包(Seo等,2007)。 

基于互补关系的蒸散发模型(Bouchet,1963)是另外一类用于估算区域蒸散发的常用模型,这类模型仅利用常规气象观测数据,不需要刻画陆面边界的详细信息。因此,此类模型避免了复杂的土壤-植被-大气这一复杂系统,不需要土壤含水量数据和植被参数(Hobbins等,2001)。不同的气候类型地区与区域水均衡的蒸发计算结果对比已经证实了该类方法的适用性(如,Hobbins等,2001;Xu和Singh,2005)。此外,此类模型认为陆表大气湿度包括了所有陆面过程的影响,已经考虑了灌溉对蒸发的影响(例如,Ozdogan和Salvucci,2004)。 

[40] Keese K E, Scanlon B R, Reedy R C. Assessing controls on diffuse groundwater recharge using unsaturated flow modeling[J]. Water Resources Research, 2005,41(6):W6010. 

[41] Climatic controls on diffuse groundwater recharge in semiarid environments of the southwestern United States
 

利用非饱和渗流模型评价地下水扩散性补给控制

        了解气候、植被和土壤对补给的控制对于估算气候变率和土地利用/土地覆盖变化对补给的潜在影响至关重要。

通过使用一维(1-D)非饱和流代码(UNSAT-H)、气候数据以及在线来源的植被和土壤覆盖率模拟5米厚剖面的排水，对补给控制进行了评估。

利用土壤传递函数从STATSGO/SSURGO土壤数据估计土壤水力特性。

植被参数由文献获取。利用德克萨斯州的数据，对13个县尺度地区进行了长期(1961-1990)模拟，这些地区代表了干旱到湿润的气候和不同的植被和土壤类型。区域平均补给速率最适合于水资源;因此，利用地理信息系统(gis)确定各区域植被与土壤组合的一维模型补给量的空间权重。裸沙模拟30年平均年补给量高(51 ~ 709 mm/yr)，占年平均降水(MAP)的23 ~ 60%(干湿)。相对于裸沙，植被的增加使补给量减少了2 ~ 30(湿润-干旱)因子，土壤结构的变化使补给量减少了2 ~ 11因子。植被和土壤结构的变化都导致了各区域内补给速率的大范围变化;然而，空间加权后，长期补给率变化较小，与MAP呈正相关(r2 = 0.85);R2 = 0.62对于可变质地的土壤)。最真实的模拟包括植被和不同质地的土壤，其补给率为0.2至118毫米/年(0.1-10%的MAP)。年平均降水量解释了80%的补给变化，可用于绘制补给图。

1. 介绍

        [2]了解水循环的控制因素，如气候、植被和土壤，对于评估气候变率和土地利用/土地覆盖(LU/LC)变化对水循环的潜在影响非常重要。目前正在区域尺度上使用陆地表面模式来评估这些影响对水循环的相对重要性[Bonan, 1997;Pielke et al, 1998]。这些模式侧重于蒸散发(ET)和陆地表面与气候之间的反馈，尚未应用于估算水循环的地下成分。

        补给(向含水层补充水)是水资源水循环的关键组成部分，也是从陆地表面向地下含水层输送营养物质和污染物的载体。为了环境目的，例如管理水资源和减少盐碱化，需要在区域范围内控制补给，这强调了了解对补给的基本控制的重要性。例子包括去除美国西南部半干旱地区的灌木和河岸植被，以增加补给，并在澳大利亚地区重新造林，以减少补给和相关的盐度问题[Allison等，1990;Dugas et al, 1998;Dawes et al, 2002;威尔科克斯,2002]。

        [3]地下水弥漫性补给的基本控制因素包括气候、植被、土壤和地形。弥漫性补给是指来自降水或灌溉的区域分布补给，应与地形洼地(如溪流、湖泊和playas)中的集中或集中补给区分开来。以往各种研究的补给估算值的比较表明，湿润地区的补给量高于干旱地区;然而，大多数研究集中在干旱区补给[Lerner et al .， 1990;知更鸟,1998]。植被的存在显著减少了半干旱到干旱流域的补给[Gee et al .， 1994]。植被类型也显著影响补给率:一年生作物和禾草区补给率高于乔木和灌木区[Prych, 1998]。在澳大利亚，用浅根作物代替深根原生桉树使补给量增加了约两个数量级(原生mallee植被为0.1 mm/年，作物/牧场轮作为5 - 30 mm/年)[Allison等，1990]。实地和模拟研究表明，相对于质地较细的土壤，较粗的土壤回灌量更大[Cook和Kilty, 1992;Rockhold et al .， 1995;Kearns and Hendrickx, 1998]。地形对补给的影响是可变的。流域尺度的模拟研究表明，在一些流域，地下横向流动可以忽略不计，流动可以被视为1-D [Dawes等，1997;哈顿,1998;Zhang等，1999]。

        [4]以前的研究通过实地研究或数值模拟来评价地下水补给的控制措施。

        Kennett-Smith等[1994]利用简单的水平衡模型和现场补给估算，研究了降水和粘土含量的补给变化。Sophocleous[1992]对堪萨斯州3400平方公里的区域进行了多元回归分析，将野外补给估算的变化主要与降水变化以及土壤储水量、地下水位深度和春季降水率的变化联系起来。Petheram等人[2002]通过回顾澳大利亚以前的补给研究，并将补给量与一年生植被和沙质土壤地区的降水相关联，评估了土地利用对补给的影响(r2 = 0.6)。然而，比较不同研究之间的补给率是困难的，因为所使用的技术种类繁多，代表了一系列的空间和时间尺度。

        [5]基于地表水、非饱和带和地下水数据，可以使用物理、化学和模拟方法来估算补给[Scanlon等，2002b]。数值模拟是唯一可以预测补给的工具，并且在隔离不同补给控制的相对重要性方面也非常有用，只要模型正确地解释了物理和生物过程。各种类型的代码可以用来模拟补给，如陆地-大气，流域，非饱和带和地下水代码。虽然陆地大气代码模拟了估算补给所需的所有过程，包括Richards的模拟不饱和流方程和各种模拟蒸散发(ET)的方法[Cotton等，2003;Dai等，2003]，这些代码通常不用于模拟补给。流域法规已用于估计地下水补给[Hatton, 1998;Zhang等，1999];然而，所需的大量参数使得难以获得唯一解。

        非饱和区码包括简单的桶码[Hatton, 1998;Hevesi et al, 2002;Lewis and Walker, 2002]到基于Richards的方程[Braud et al, 1995;Fayer等人，1996年]，以及一些包括植物生长模块[Dawes和Hatton, 1993;Zhang等，1996]。利用非饱和带代码对裸地进行补给的模拟研究[Scanlon和Milly, 1994;Scott等人，2000]到植被系统[Rockhold等人，1995;Kearns and Hendrickx, 1998]。一维非饱和带模型已与植被和土壤的GIS覆盖范围一起用于确定区域分布的补给[Fayer等，1996]。使用非饱和带代码评估补给控制的敏感性分析相当简单，范围从整体到简单的双层土壤剖面，有无植被和不同的植被类型(灌木/草)[Rockhold等，1995;Kearns and Hendrickx, 1998]。地下水模型校正或反演也可用于估算补给速率;然而，利用水头数据进行模型反演仅限于估算补给与水力导电性的比率[Sanford, 2002]。这种补给估计通常不被认为是高度可靠的，因为水力导电性可以在几个数量级上变化。

        更可靠的补给估算除了水头外，还需要关于水通量或年龄的信息来校准模型[Sanford, 2002]。

        [6]建模补给的主要困难是数据要求和模型参数化。以下在线数据源使充值模拟更加可行。天气生成器，如GEM(生成多种应用的天气要素)，包括气象站数据库，可以生成其他地区的数据[Hanson等，1994;理查森,2000]。

        土壤的地理信息系统(GIS)分布由国家土壤地理(STATSGO)数据库(1:25万比例尺)和土壤调查地理(SSURGO)数据库(1:24万比例尺)提供。土壤传递函数可用于将土壤质地信息转化为建模所需的保水性和水力特性[Schaap等，2001]。植被分布和土地利用(National land Cover Data)可从网上获取[McMahon et al .， 1984;Vogelmann等人，2001]。遥感还提供不同分辨率的植被参数信息(30米;LandSat TM至1.1公里;MODIS)。可利用AVHRR或MODIS等卫星数据从植被覆盖度中估算出光秃秃面积的百分比。叶面积指数的信息来源于归一化植被指数(NDVI) [Myneni等，1997]。获取生根深度的信息较为困难;然而，可以从文献中获得估计[例如，Canadell等人，1996]。

[7]本研究的目的是在德克萨斯州的数据基础上，利用代表一系列气候(干旱-湿润)、植被(灌木、草、森林、作物)和土壤(细-粗粒度、整体和分层)条件的区域的非饱和一维补给流模型，确定不同控制措施对弥漫性地下水补给的相对重要性。本研究的重点是长期(30年)的实际平均补给率，这适用于评估水资源和评估含水层对养分负荷的脆弱性。该研究的独特之处在于:(1)研究的气候、植被和土壤条件的范围;(2)使用在线和已发布的数据作为模型的输入和参数化;(3)将1- d建模和GIS覆盖相结合，以开发区域平均补给估算;(4)模拟的长度(1961 - 1990);(5)与实地估算的比较。

2. 材料与方法

2.1. 研究区域描述:气候、土壤和植被

[8] The broad study area is the state of Texas (»700,000 km2 ) (Figure 1). Thirteen study regions, representing a variety of climate, vegetation, and soil types were used in this study to simulate the water balance for a 30 year period (1961 – 1990). Simulated regions were also located to represent recharge areas of major porous media aquifers in the state (Figure 1 and Table 1). Each study region represents a one- or two-county area above an aquifer (1152– 3042 km2 ), with the exception of region 2 (entire outcrop of Cenozoic Pecos Alluvium Aquifer: 14,980 km2 ). The topography of the regions is generally flat, with average slopes º0.5% in the High Plains and Gulf Coast regions and slightly higher slopes in the remaining regions (º1.3%) (Table 1). Long-term (1961 – 1990) mean annual precipitation (MAP) ranges from 224 mm/yr in the west to 1,184 mm/yr in the east. Annual precipitation at individual meteorological stations ranged from 110 mm (region 1, El Paso, 1969) to 1783 mm (region 13, Houston, 1973). Summer precipitation (June –August) is dominant throughout much of the state, particularly in western (43%) and northern (33 – 48%) regions (Figure 2). Spring precipitation is dominant in central regions (29 – 33%), whereas fall precipitation is dominant in southeastern regions (28 – 39%). Precipitation is fairly uniformly distributed in the more humid regions in the east. Winter precipitation (December–February) is generally low throughout most of the state (8 – 16%), with the exception of the humid east (21%). The coefficient of variation (CV) in annual precipitation is greatest in semiarid regions in the west (0.35) and less throughout the rest of the area (CV: 0.21 –0.24) (Figure 3 and Table 2). Vegetation ranges from predominantly shrubs and grasses in the west, shrub/forest to forest/shrub in the central area, and forest and forest/ shrub in the east (Figure 4). Cropland areas dominate much of the northern and southeastern regions. Variations in clay content in the upper 1.5 to 2 m soil profile depths based on STATSGO data generally follow the distribution of underlying geologic units, e.g., high clay content in the central region of the Southern High Plains (region 5), corresponding to the underlying Blackwater Draw Formation, and high clay content in the northern and central parts of the Gulf Coast (regions 12 and 13), corresponding to the underlying Beaumont Formation (Figure 5).

2.2. Model Description 

[9] Unsaturated flow modeling was used to simulate drainage below the root zone, which is equated to groundwater recharge and assumes that climate and land use/land cover remain constant over timescales required for water to move from the root zone to the water table. The UNSAT-H code (version 3.0 [Fayer, 2000]) was chosen because previous code comparison studies showed that water balance simulations based on UNSAT-H compare favorably with field data [Scanlon et al, 2002a]. UNSAT-H is a 1-D, finite difference code that simulates nonisothermal liquid flow and vapor diffusion in response to meteorological forcing. The simulations focus on the water balance:

where D is deep drainage below the root zone, P is precipitation, ET is evapotranspiration, R0 is surface runoff, and ΔS is change in water storage. UNSAT-H simulates subsurface water flow using Richards’ equation:

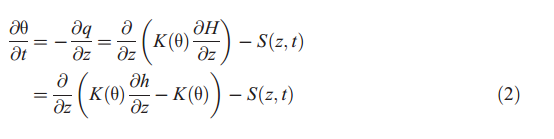
where θ is volumetric water content, q is water flux, K is hydraulic conductivity, H is hydraulic head, h is matric potential head, and S is a sink term used to describe the removal of water by plants. UNSAT-H includes multiple analytical functions for water retention and unsaturated hydraulic conductivity.

[10] The upper atmospheric boundary condition is simulated as a system-dependent boundary condition that changes from a prescribed head to a prescribed flux, depending on climate and subsurface conditions. If the applied flux (precipitation or evapotranspiration) is º the potential flux and the matric potential head at the surface is between 0 and a prespecified dry value (hdry), then the potential flux, which is controlled by external conditions, applies. Runoff is simulated implicitly by UNSAT-H. If the precipitation rate exceeds the infiltration capacity of the soil, excess water runs off (infiltration excess or Hortonian runoff). If the matric potential head at the surface reaches 0, the soil becomes saturated, a constant head boundary condition applies (h = 0), and excess water runs off (saturation excess or Dunne runoff). If the soil surface becomes too dry (h º hdry), a constant head boundary condition applies (h = hdry) and evaporation or evapotranspiration is controlled by the rate at which water can be transmitted to the surface. Ponding is not simulated with this code. Plant water uptake is simulated according to the approach proposed by Feddes et al [1978] that partitions PET into potential evaporation (PE) and potential transpiration (PT) using an empirical equation developed by Ritchie and Burnett [1971], which distributes PT over the root zone on the basis of depth variations in root density and reduces this PT to actual transpiration on the basis of matric potential head [Fayer, 2000].

2.3. Model Application [11] The water balance for a 30 year period (1961 –1990) was simulated for 13 study regions. Input data requirements for the model include meteorologic forcing, vegetation parameters, hydraulic parameters for different soil types, and initial conditions. To assess the relative importance of different controls on groundwater recharge, four different scenarios were used: (1) nonvegetated, monolithic sand, (2) nonvegetated, texturally variable soil, (3) vegetated, monolithic sand, and (4) vegetated, texturally variable soil.

The simplest simulations of nonvegetated, monolithic sand were used to provide an upper bound on recharge rates.

Complex, texturally variable soil profiles were simulated without vegetation to evaluate the impact of soil textural variability on recharge. Vegetation was added to the monolithic and texturally variable soil profiles to determine its impact on simulated recharge. The most realistic scenario is represented by vegetated, texturally variable soils.

[12] A soil-profile depth of 5 m was chosen for the simulations because it is deeper than root zone depths of the vegetation used. In addition, soil textural information is available only for the upper 2 m from STATSGO and SSURGO, and texture in the 2 to 5 m zone was assumed equal to that of the lowest data available. Sensitivity of simulated recharge to profile depth was evaluated. In monolithic profiles, nodal spacing ranged from 2 mm at the top and base of the profile and increased by a factor of »1.2 with depth to a maximum value of 230 mm within the profile. In layered soil profiles, nodal spacing was also reduced near textural interfaces to a value of »20 mm.

Initial conditions were set arbitrarily at a matric potential head of ½3 m for higher precipitation regions (6 – 13) and ½10 m for all other regions. The impact of initial conditions on simulation results was evaluated by reinitializing simulations multiple times with the final conditions of each run; however, rerunning simulations once was found to be sufficient for minimizing the impact of initial conditions.

[13] Meteorological data for 10 stations were obtained from the database in the GEM code [Hanson et al, 1994].

Some station data were used to simulate recharge in more than one region (Midland station, regions 2 and 3; Fort Worth station, regions 9 – 11). The 1961 – 1990 period was chosen because of availability of solar radiation for potential evapotranspiration calculations from the National Solar Radiation Data Base (National Renewable Energy Laboratory, Golden, Colorado; 1992). Meteorologic input to the model included daily precipitation, daily average dew point temperature, wind speed and cloud cover, total daily solar radiation, and minimum and maximum daily temperatures.

Daily precipitation was applied at a prespecified default intensity of 10 mm/hr, and ET is not simulated during this time. Previous code comparisons showed that the approach used in codes to simulate precipitation and evapotranspiration when daily precipitation is used as input can have a large impact on simulated recharge and that the UNSAT-H approach adequately simulates measured data [Scanlon et 

al., 2002a]. A modified Penman-Monteith equation was used to calculate PET [Doorenbos and Pruitt, 1977].

Parameter hdry was set to ½100 m. A unit gradient lower boundary condition was used that corresponds to free drainage or gravitational flow and is most appropriate for simulating unimpeded recharge.

[14] Distribution of vegetation types for each of the modeled regions was obtained from a GIS coverage of vegetation in Texas [McMahon et al, 1984] (Figures 4 and 6). Crop vegetation types were derived from the percentage of area harvested over the simulation period (USDA National Agricultural Statistics Service). Vegetation parameters required for UNSAT-H include percent bare area, planting and harvesting dates for crops, time series of leaf area index (LAI) and rooting depth (RD), and root length density (RLD). These parameters were obtained mostly from the literature (see auxiliary material).1 Additional information was obtained from discussions with ecologists and crop specialists. Time series for LAI and root growth were specified on particular days of the year and linearly interpolated. Root growth was simulated for crops only; other plant types were perennial. The RLD function is based on the assumption that normalized total root biomass is related directly to RLD (rrL) and can be related to depth below the surface (z) by 

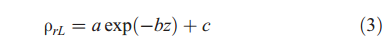
where a, b, and c are coefficients that optimize fit to normalized biomass data. Some vegetation classes contain more than one vegetation type. For example, forests are classified as 75% trees and 25% grasses. Recharge estimates for these regions were obtained by simulating different vegetation types separately and areally weighting results.

The 1-D modeling approach used in this study does not account for effects of neighboring plant root systems and may overestimate recharge in areas where deeper rooted vegetation extends into areas with shallower rooted vegetation. Recharge would be overestimated most in areas where the difference in rooting depths is greatest. However, this error is considered relatively minor considering that information on the distribution of different vegetation types is only approximate. Dominant vegetation types that represented »70– 80% of the area of each region were simulated.

[15] Soil profiles for the simulations ranged from monolithic sand to texturally variable profiles. Hydraulic properties for the sand were obtained from the UNSODA database (UNSODA 4650: Ks: 5.87 m/day; qs: 0.38; qr: 0; a: 5.03 1/m; n: 1.7736 [Leij et al, 1996]). SSURGO version 2 data [U.S. Department of Agriculture (USDA), 1994] were used to provide information for texturally variable soil profiles for all regions but were unavailable for region 2, where STATSGO data [USDA, 1995] were used for the entire (multicounty) outcrop area of the aquifer. Pedotransfer functions were used to determine soil hydraulic properties.

Rosetta software uses neural network programming and a database of measured texture, water retention, and saturated hydraulic conductivity to provide estimates of van 

Genuchten water retention parameters and saturated hydraulic conductivity for input to unsaturated flow models [Schaap et al, 2001]. Only texture and bulk density information was available from the STATSGO database for input to Rosetta. Soil layer texture, bulk density, and volumetric water content at ½3 and ½150 m head were available from the SSURGO version 2 database for input to Rosetta. Simulations were run for soil profiles that represented »80% of the area of each simulated region, which corresponded to 6– 29 profiles for different regions. Examination of recharge results for all profiles for a region showed that recharge rates could be categorized into distinct groups, resulting in a more manageable 3 – 7 representative profiles for each region.

[16] Simulated recharge results are represented by a single temporal (30 year) and spatial average recharge value for each region, using GIS coverages to determine the area represented by each vegetation type, soil type, or combination of vegetation and soil types to spatially weight 1-D results. A total of 460 simulations were conducted for the final analysis. For monolithic profile simulations, models were developed for each of the 10 meteorological stations, resulting in 10 representative recharge values. For vegetated and texturally variable soil profile simulations, 13 recharge values representative of each of the study regions were determined. Recharge rates for each region (30 year, spatially weighted average) were plotted versus long-term (30 year) MAP, and equations were fit to the results for each of the four modeling scenarios (i.e., nonvegetated monolithic and texturally variable soil profiles and vegetated monolithic and texturally variable soil profiles). Power law equations were used because they resulted in higher correlation coefficients and lower residual standard deviations than linear or log linear equations. Finally, the power law equation representing the vegetated, texturally variable soils scenario was used to generate a continuous statewide recharge rate map based on the distribution of MAP.

Although shown for the entire state, results should be applied only to outcrop areas of the porous media aquifers shown.

[17] Sensitivity of recharge to climate, vegetation, and soils was evaluated in the four different scenarios considered, isolating the impact of each of these parameters.

Additional sensitivity analyses were conducted to evaluate variations in vegetation parameters, initial conditions, PET, and depth of soil profile. Vegetation parameters evaluated included percent bare area, leaf area index, root depth, and root length density. Each parameter was increased and decreased by 50 percent, with the exception of percent bare area, which is 0 for the base case and was increased to 25 and 50%, and profile depth, which was increased from 5 to 10 m in the sensitivity analysis. Sensitivity analyses were conducted using data from region 6.

3. Results and Discussion [18] Simulation results are represented for the four basic scenarios to assess relative importance of climate, vegetation, and soils in controlling recharge. Final mass balance errors were <5% of final recharge rates and <0.5 mm/yr.

3.1. Nonvegetated, Monolithic Sand Simulations [19] Simulated mean (30 year) annual recharge for bare sand is high and ranges from 51 mm/yr in the arid west to 709 mm/yr in the more humid east, representing 23 (arid) to 

60% (humid) of MAP (Table 2). Variations in mean annual recharge can be explained entirely by variations in MAP, using the power law relationship. Recharge increases with precipitation (r2 = 1.0; Figure 7 and Tables 2 and 3). These recharge estimates provide an upper bound on actual recharge rates because vegetation and soil textural variability were not included. In addition, simulated runoff from the 1-D model is zero, whereas runoff estimates based on a statewide water balance range from 0 mm/yr in the west to 415 mm/yr in the east [Reed et al, 1997]. Lack of simulated runoff was attributed to the high saturated hydraulic conductivity of the sand (0.24 m/hr) relative to the prespecified precipitation intensity (0.01 m/hr).

[20] Temporal variability in mean annual recharge is similar throughout the state (CV: 0.16 –0.24) and is less than that of precipitation (Table 2). Lower correlations between mean annual recharge and summer precipitation (r2 = 0.66) relative to precipitation during the other seasons (r2 = 0.83– 0.96 for spring, fall, and winter) were attributed to higher evaporation during summer (Figures 2 and 8).

Potential ET is much greater than simulated actual E; the PET/AE ratio decreased from 12.1 in the west (region 1) to 

2.9 in the east (region 13) (Table 2). In arid regions most infiltrated water is returned to the atmosphere through evaporation, as shown by the tracking of precipitation and evaporation in region 1 (Figure 9). The high correlation (r2 = 0.83) between evaporation and precipitation in this region may be attributed to evaporation rarely being energy limited (high PET). Annual recharge is not directly correlated with annual precipitation (r2 = 0.03) because there is a lag between elevated precipitation and recharge. In contrast, in more humid settings evaporation and precipitation are not as highly correlated (r2 = 0.66, region 13), which may be related to energy limitations on ET (lower PET). There is little lag between high precipitation and recharge, as shown by the strong correlation between annual precipitation and recharge (r2 = 0.90, region 13).

3.2. Nonvegetated, Texturally Variable Soil Simulations [21] Simulated mean (30 year) annual, areally averaged recharge ranges from 16 mm/yr in the north to 230 mm/yr in the southeast for texturally variable soil profiles, representing 3 to 29% of MAP (Figure 7 and Table 2). These recharge rates are 2 to 11 times lower than those based on monolithic sand profiles, indicating the importance of soil textural variability in controlling recharge. The lower recharge rates may reflect finer textured soils, or they may be related to reductions in recharge caused by profile layering, both fine over coarse (capillary barrier effect) and coarse over fine layering. Reductions in recharge in the texturally variable soil simulations correspond to increased runoff, evaporation, or both. Approximately 60% of the variation in recharge can be explained by variations in precipitation using the power law relationship (r2 = 0.62, Table 3). Multiple linear regression using log-log data shows that including clay content (profile average) with precipitation explains 80% of the variation in recharge.

Recharge varies over 1 to 2 orders of magnitude locally, within each region, because of textural variability among soil profiles.

[22] Variations in simulated mean (30 year) annual runoff generally reflect differences in climate and texture among regions. Simulated runoff is positively correlated with mean clay content (r2 = 0.57) and negatively correlated with mean sand content (r2 = -0.49). Sandy areas, particularly regions 1, 2, 3, and 7, have low runoff and generally correspond to areas of low or moderate precipitation. Most regions with clay-rich soils have higher runoff and generally overlie finegrained geologic units. Simulated recharge rates in clay-rich soils may not accurately reflect actual recharge rates if preferential flow occurs in these settings because this process is not included in the simulations.

3.3. Vegetated, Monolithic Sand Simulations [23] To assess the impact of vegetation without the influence of soil textural variability, simulations of recharge were conducted in vegetated, monolithic sands (Table 2).

Vegetation markedly reduces simulated mean annual recharge (2 – 369 mm/yr; 1– 31% of MAP) by factors of 2 to 30 relative to recharge for nonvegetated simulations.

MAP explains 85% of the variance in simulated recharge using the power law relationship (Table 3 and Figure 7).

Simulated runoff was 0 for nonvegetated and vegetated simulations. Vegetation type also affects simulated recharge, as seen in the 1 to 2 orders of magnitude range in simulated recharge for different vegetation types within a study region. In general, lower recharge rates in areas with trees relative to grasses can be attributed to greater rooting depth of trees (º4.3 m) relative to grasses (1 m). Shrubs are generally more effective than crops in reducing recharge because of greater rooting depth and longer growing season.

Crops also differ in their recharge rates: e.g., factor of 4 lower recharge beneath cotton (maximum rooting depth 2.1 m) relative to sorghum (maximum rooting depth 1.5 m), in region 4.

3.4. Vegetated, Texturally Variable Soil Simulations [24] Texturally variable soils with vegetation are the most realistic representation of actual conditions and should provide the most reliable recharge estimates for the different regions. Simulated mean (30 year) annual, areally averaged recharge is lowest in the arid west (0.2 mm/yr) and highest in the humid east (118 mm/yr), representing 0.1 to 10% of MAP (Figure 7 and Table 2). Variability of MAP explains 80% of the variability in recharge among regions using the power law relationship (r2 = 0.81, Table 3). The correlation between recharge and precipitation was used to map recharge throughout the entire study area (Figure 10).

[25] Vegetation markedly reduced recharge relative to that for nonvegetated, texturally variable soils. Reduction factors were greater in more arid regions in the west (7 –78) relative to more humid regions in the east (2– 31) and reflect the enhanced ability of vegetation to reduce recharge in more water-limited regions (Table 2). Local variability in simulated recharge within regions was generally within an order of magnitude and reflects variability due to differences in vegetation and soil texture.

[26] Simulated mean (30 year) annual runoff and runoff estimates based on measured stream gauge data (1961 – 1990) used to develop a statewide water balance [Reed et al, 1997] are generally consistent in many regions considering that the 1-D modeling approach does not account for subsurface lateral flow and routing (Table 4). Discrepancies between the two estimates in other regions cannot readily be explained, with the exception of regions 4 and 5 in the Southern High Plains, where overestimation of runoff may be attributed to predominantly internal drainage to ephemeral lakes or playas and little runoff to gauged stream networks. Runoff is one of the most difficult parameters to simulate because it depends on accurate representation of rainfall intensity and hydraulic conductivity of surficial sediments that may be crusted, as shown by detailed comparisons of simulated and measured runoff at a controlled field experiment [Scanlon et al, 2002a].

[27] Relative controls of different vegetation types in vegetated, texturally variable soil simulations are similar to those for vegetated monolithic sands: lower recharge in deep-rooted trees relative to shallow-rooted grasses, shrubs relative to crops, and cotton relative to sorghum. For example, in region 9, simulated recharge beneath trees is 0, whereas simulated recharge beneath grasses ranges from 1 to 156 mm/yr for different soils. Relative amounts of evaporation and transpiration vary with vegetation type and soil texture. Transpiration is much greater than evaporation for trees, irrespective of texture. Evaporation is higher than transpiration in finer textured soils than in coarser textured soils, irrespective of vegetation type, which is attributed to finer textured soils retaining more water near the soil surface longer, allowing greater evaporation.

3.5. Sensitivity Analyses [28] Sensitivity analyses were conducted for region 6 because it represents average climate and soil conditions in the study area. Sensitivity of simulated recharge to different vegetation parameters is variable (Table 5). Increasing percent bare area from 0 to 50% increases recharge up to a factor of 8. Simulated recharge is inversely related to root depth because decreasing root depth allows water to drain more readily below the root zone. Decreasing root depth increases recharge by factors of 2 to 5, whereas increasing root depth decreases recharge by factors of 0.2 to 0.5. Simulated recharge is more sensitive to decreasing  

LAI than increasing LAI. Decreasing LAI by 50% almost doubles recharge, while increasing LAI by 50% decreases recharge by 20%. Models were insensitive to variations in root-length density. Decreasing PET increases recharge by factors ranging from 4 in coarse-grained soils to 38 in finegrained soils and was balanced by a reduction in ET, whereas increasing PET had the opposite effect.

[29] It is important to assess sensitivity of model output to variations in initial conditions, profile depth, and equilibration times to assess reliability of simulated recharge. The model is insensitive to variations in initial conditions.

Increasing profile depth from 5 to 10 m decreases recharge in coarse-grained soils by a factor of 0.9 and increases recharge by a factor of 1.2 in fine-grained soil, which may be an artifact of drainage of initial water in the profile.

Model equilibration times are greater for more arid settings and more clay-rich soils. Therefore final recharge estimates in these settings may represent an upper bound on actual recharge rates.

3.6. Comparison of Simulated Recharge Estimates With Those Based on Other Techniques [30] Simulated recharge rates from this study were compared with those based on earlier studies (Table 6). Previous field and modeling investigations in the Chihuahuan Desert in west Texas indicate that there is no recharge in interdrainage settings [Scanlon et al, 1999], which is generally consistent with the low (0.2 mm/yr) simulated recharge in this study (Table 2). Bulge-shaped chloride profiles and upward matric potential gradients indicate that this system has been drying out for the last 10,000 to 15,000 years since the Pleistocene [Scanlon et al, 2003a].

[31] In the Southern High Plains, it is difficult to compare simulated recharge rates from this study, which represent diffuse recharge in interdrainage settings, with previous recharge estimates from groundwater data because most recharge in this region is focused beneath playas.

Therefore simulated recharge at regions in the Southern High Plains (4 and 5) (0.4 – 0.8 mm/yr) is less than recharge estimates based on the chloride mass balance (CMB) approach applied to groundwater (11 mm/yr [Wood and Sanford, 1995]), as expected. Field studies indicate that there is no recharge in natural ecosystems in interplaya settings, as shown by chloride bulges and upward matric potential gradients [Wood and Sanford, 1995; Scanlon and 

Goldsmith, 1997; Dennehy et al, 2005]. Recharge estimates based on chloride profiles from nonirrigated cultivated settings in the south part of the Southern High Plains range from 4 to 28 mm/yr [Scanlon et al, 2003b].

Simulated recharge rates at regions 3 and 4 (1.5 and 0.8 mm/yr) fall within the range of values for natural and cultivated regions and may underestimate actual recharge because the effect of cultivation on hydraulic properties of surficial sediments was not included in the simulations.

[32] Simulated recharge in region 6 (5.6 mm/yr) is within the lower range of field-based estimates, using the CMB approach applied to the unsaturated zone (UZ) in natural and nonirrigated cultivated regions (5 – 30 mm/yr) [Scanlon et al, 2003b]. Higher values from the field studies may be attributed to restriction of field regions to a large sand dune setting, whereas the spatially averaged value from this modeling study also includes finer grained soils found in other regions.

[33] Simulated recharge at region 8 (10.1 mm/yr) is within the range of field-based recharge estimates based on the chloride mass balance (CMB) approach applied to the unsaturated zone and groundwater (5 – 20 mm/yr [Dutton et al, 2003]). Recharge estimates based on the CMB approach applied to groundwater for region 11 range from 43 to 71 mm/yr and are slightly higher than that simulated (35.1 mm/yr). The discrepancy may be attributed to bias toward high-permeability units in field-based estimates.

[34] Although the number of comparisons between simulated and field-based recharge estimates is limited, simulated recharge rates in this study are generally consistent with those based on previous field studies, and discrepancies can generally be explained by inclusion or exclusion of different types of recharge (e.g., focused versus diffuse recharge in the Southern High Plains) and concentrating on different zones (e.g., high-permeability versus lowpermeability units).

3.7. Recommendations for Future Studies [35] This study represents a relatively simple approach to estimating recharge using a 1-D unsaturated flow model and data found online and in the literature. Future simulations should consider using actual precipitation intensity where data are available and develop input to simulate recharge in irrigated regions. The most fundamental conceptual aspect of unsaturated flow modeling that should be addressed is simulation of vegetation dynamics. Current simulations prescribe vegetation input that precludes vegetation response to variability in soil moisture and precipitation. Two-way coupling between vegetation growth and soil moisture variability related to climate should provide more realistic simulations of recharge, particularly in semiarid –arid regions. In addition, representation of the continuum of roots and various rooting depths associated with vegetation communities is essential for reliable recharge estimation.

3.8. Implications for Water Resources

[36] Reliable recharge estimates are critical for evaluation of and optimal management of water resources. Long-term average recharge rates are beneficial to groundwater managers because management plans are developed generally for decadal timescales. The relationship between precipitation and recharge developed in this study for vegetated, 

texturally variable soils was used to map spatial variability of recharge for the groundwater model of the CarrizoWilcox aquifer in Texas [Kelley et al, 2004]. Scaling factors were developed for the groundwater model that varied these recharge rates with topography and subsurface geology with high recharge in upland areas and above more permeable geologic units, similar to the B value discussed by Hatton [1998].

[37] Understanding of climatic and vegetation controls on groundwater recharge shown by simulations in this study can be used to assess potential impacts of climate variability and land use/land cover change on groundwater availability by using space as a proxy for time. The effect of vegetation types on simulated recharge can be used to provide preliminary estimates of potential impacts of removing invasive woody species in many areas of Texas. The state is currently investing millions of dollars in this program to increase water availability [Wilcox, 2002].

4. Conclusions [38] 1. Unsaturated zone modeling using online data is a useful approach for simulating diffuse recharge in porous media systems from point to regional scales where input data are available.

[39] 2. Climate, vegetation, and soils each exert controls on groundwater recharge. (1) High simulated long-term (30 year) mean annual recharge (51 – 709 mm/yr) in nonvegetated sandy profiles represents 23 to 60% (arid – humid) of MAP and provides an upper bound on actual recharge. (2) Soil textural variability controls recharge, as shown by the large reduction by factors of 2 to 11 in simulated recharge for nonvegetated, texturally variable soils relative to those in monolithic sands. (3) Presence and type of vegetation control recharge, as shown by the reduction in recharge in vegetated relative to that in nonvegetated monolithic sand (factors of 2 – 30, humid –arid) and vegetated relative to that in nonvegetated, texturally variable soil (factors of 2 – 80, humid –arid). Relative reductions in recharge due to vegetation were greater in semiarid –arid relative to more humid regions and reflect the enhanced ability of vegetation to reduce recharge in more water-limited regions.

[40] 3. The most realistic long-term (30 year) recharge estimates based on vegetated, texturally variable soils range from 0.2 to 118 mm/yr, representing 0.1 to 10% (arid – humid) of long-term MAP.

[41] 4. Approximately 80% of the variability in simulated recharge can be explained by variability in MAP in vegetated, layered soil profiles using the power law relationship.

MAP can be used as a predictor of mean annual recharge.

[42] 5. Simulated long-term, spatially averaged recharge rates generally compare favorably with recharge estimates based on previous field studies.

[43] 6. Simulated long-term (30 year), spatially averaged runoff is generally within the range of estimates based on gauge data in statewide water balance modeling for most regions. Discrepancies in the Southern High Plains can be explained by internal drainage to playas.

[44] 7. Unsaturated zone modeling provides a valuable tool for isolating controls on groundwater recharge. Understanding these controls can be used to assess potential impacts of climate variability and land use/land cover change on groundwater recharge.

References Allison, G. B., P. G. Cook, S. R. Barnett, G. R. Walker, I. D. Jolly, and M. W. Hughes (1990), Land clearance and river salinisation in the western Murray Basin, Australia, J. Hydrol., 119, 1 – 20.

Bonan, G. B. (1997), Effects of land use on the climate of the United States, Clim. Change, 37, 449 – 486.

Braud, I., A. C. Dantas-Antonino, M. Vauclin, J. L. Thony, and P. Ruelle (1995), A simple soil-plant-atmosphere transfer model (SiSPAT) development and field verification, J. Hydrol., 166, 213 – 250.

Canadell, J., R. B. Jackson, J. R. Ehleringer, H. A. Mooney, O. E. Sala, and E.-D. Schulze (1996), Maximum rooting depth of vegetation types at the global scale, Oecologia, 108, 583 – 595.

Cook, P. G., and S. Kilty (1992), A helicopter-borne electromagnetic survey to delineate groundwater recharge rates, Water Resour. Res., 28, 2953 – 2961.

Cotton, W. R., et al (2003), RAMS 2001: Current status and future directions, Meteorol. Atmos. Phys., 82, 5 – 29.

Dai, Y. X., et al (2003), The Common Land Model (CLM), Bull. Am.

Meteorol. Soc., 84, 1013 – 1023.

Dawes, W. R., and T. J. Hatton (1993), TOPOG_IRM, 1, model description, Tech. Memo. 93/5, Div. of Water Resour., Commonw. Sci. and Ind. Res.

Organ., Canberra.

Dawes, W. R., L. Zhang, T. J. Hatton, P. H. Reece, G. T. H. Beale, and I. Packer (1997), Application of a distributed parameter ecohydrological model (TOPOG_IRM) to a small cropping rotation catchment, J. Hydrol., 191, 67 – 89.

Dawes, W. R., M. Gilfedder, M. Stauffacher, J. Coram, S. Hajkowicz, G. R.

Walker, and M. H. Young (2002), Assessing the viability of recharge reduction for dryland salinity control: Wanilla, Eyre Peninsula, Aust.

J. Soil Res., 40, 1407 – 1424.

Dennehy, K. F., B. W. Bruce, and C. A. McMahon (2005), Evaluation of recharge beneath irrigated and natural settings in the Southern High Plains, U.S. Geol. Surv. Water Resour. Invest. Rep., in press.

Doorenbos, J., and W. O. Pruitt (1977), Guidelines for Predicting Crop Water Requirements, Irrig. Drain. Pap. 24, 2nd ed., 144 pp., Food and Agric. Organ., Rome.

Dugas, W. A., R. A. Hicks, and P. Wright (1998), Effect of removal of Juniperus ashei on evapotranspiration and runoff in the Seco Creek watershed, Water Resour. Res., 34, 1499 – 1506.

Dutton, A. R., B. Harden, J. P. Nicot, and D. O’Rourke (2003), Groundwater availability model for the central part of the Carrizo-Wilcox aquifer in Texas, contract report, Tex. Water Dev. Board, Austin.

Fayer, M. J. (2000), UNSAT-H version 3.0: Unsaturated soil water and heat flow model, theory, user manual, and examples, Rep. PNNL-13249, Pac.

Northwest Natl. Lab., Richland, Wash.

Fayer, M. J., G. W. Gee, M. L. Rockhold, M. D. Freshley, and T. B. Walters (1996), Estimating recharge rates for a groundwater model using a GIS, J. Environ. Qual., 25, 510 – 518.

Feddes, R. A., P. J. Kowalik, and H. Zaradny (1978), Simulation of Field Water Use and Crop Yield, 189 pp., PUDOC, Wageningen, Netherlands.

Gee, G. W., P. J. Wierenga, B. J. Andraski, M. H. Young, M. J. Fayer, and M. L. Rockhold (1994), Variations in water balance and recharge potential at three western desert sites, Soil Sci. Soc. Am. J., 58, 63 – 71.

Hanson, C. L., K. A. Cumming, D. A. Woolhiser, and C. W. Richardson (1994), Microcomputer program for daily weather simulation, Publ.

ARS-114, 38 pp., Agric. Res. Serv., U.S. Dep. of Agric., Washington, D. C.

Hatton, T. J. (1998), The Basics of Recharge and Discharge, part 4, Catchment Scale Recharge Modeling, Commonw. Sci. and Ind. Res. Organ., Collingwood, Victoria, Australia.

Hevesi, J. A., A. L. Flint, and L. E. Flint (2002), Preliminary estimates of spatially distributed net infiltration and recharge for the Death Valley Region, Nevada-California, U.S. Geol. Surv. Water Resour. Invest.

Rep., 02-4010, 36 pp.

Kearns, A. K., and J. M. H. Hendrickx (1998), Temporal variability of diffuse groundwater recharge in New Mexico, Tech. Rep. No. 309, 43 pp., N.M. Water Resour. Res. Inst., Soccoro.

Kelley, V., N. Deeds, and J. P. Nicot (2004), Groundwater availability model of the Queen City Sparta Aquifer, contract report, Tex. Water Dev. Board, Austin.

Kennett-Smith, A., P. G. Cook, and G. R. Walker (1994), Factors affecting groundwater recharge following clearing in the south western Murray Basin, J. Hydrol., 154, 85 – 105.

Leij, F. J., W. J. Alves, M. T. van Genuchten, and J. R. Williams (1996), The UNSODA unsaturated soil hydraulic database, user’s manual, version 1.0, Rep. EPA/600/R-96/095, Natl. Risk Manage. Lab., U.S.

Environ. Prot. Agency, Cincinnati, Ohio.

Lerner, D. N., A. S. Issar, and I. Simmers (1990), Groundwater Recharge, Intl. Assoc. of Hydrogeol., Kenilworth, U. K.

Lewis, M. F., and G. R. Walker (2002), Assessing the potential for episodic recharge in south-western Australia using rainfall data, Hydrogeol. J., 10, 229 – 237.

McMahon, C. A., R. G. Frye, and K. L. Brown (1984), The vegetation types of Texas including cropland, Bull. 7000-120, 40 pp., Texas Parks and Wildlife Dep., Austin.

Myneni, R. B., R. R. Nemani, and S. W. Running (1997), Estimation of global leaf area index and absorbed PAR using radiative transfer models, IEEE Trans. Geosci. Remote Sens., 35, 1380 – 1393.

Petheram, C., L. Zhang, G. R. Walker, and R. Grayson (2002), Towards a framework for predicting impacts of land-use on recharge: 1. A review of recharge studies in Australia, Aust. J. Soil Res., 40, 397 – 417.

Pielke, R. A. S., R. Avissar, M. Raupach, A. J. Dolman, X. Zeng, and A. S.

Denning (1998), Interactions between the atmosphere and terrestrial ecosystems: Influence on weather and climate, Global Change Biol., 4, 461 – 475.

Prych, E. A. (1998), Using chloride and chlorine-36 as soil-water tracers to estimate deep percolation at selected locations on the U.S. Department of Energy Hanford Site, Washington, U.S. Geol. Surv. Water Supply Pap., 2481, 67 pp.

Reed, S. M., D. R. Maidment, and J. Patoux (1997), Spatial water balance of Texas, Tech. Rep. 97-1, Cent. for Res. in Water Resour., Univ. of Tex.

at Austin, Austin.

Richardson, C. W. (2000), Data requirements for estimation of weather generation parameters, Trans. ASAE, 43, 877 – 882.

Ritchie, J. T., and E. Burnett (1971), Dryland evaporative flux in a subhumid climate 2. Plant influences, Agron. J., 63, 56 – 62.

Robins, N. S. (1998), Groundwater Pollution, Aquifer Recharge and Vulnerability, Geol. Soc. Spec., 130.

Rockhold, M. L., M. J. Fayer, C. T. Kincaid, and G. W. Gee (1995), Estimation of natural ground water recharge for the performance assessment of a low-level waste disposal facility at the Hanford site, Rep.

PNL-10508, Pac. Northwest Natl. Lab., Richland, Wash.

Sanford, W. (2002), Recharge and groundwater models: An overview, Hydrogeol. J., 10, 110 – 120.

Scanlon, B. R., and R. S. Goldsmith (1997), Field study of spatial variability in unsaturated flow beneath and adjacent to playas, Water Resour.

Res., 33, 2239 – 2252.

Scanlon, B. R., and P. C. D. Milly (1994), Water and heat fluxes in desert soils: 2. Numerical simulations, Water Resour. Res., 30, 721 – 733.

Scanlon, B. R., R. P. Langford, and R. S. Goldsmith (1999), Relationship between geomorphic settings and unsaturated flow in an arid setting, Water Resour. Res., 35, 983 – 999.

Scanlon, B. R., M. Christman, R. C. Reedy, I. Porro, J. Simunek, and G. Flerchinger (2002a), Intercode comparisons for simulating water balance of surficial sediments in semiarid regions, Water Resour. Res., 38(12), 1323, doi:10.1029/2001WR001233.

Scanlon, B. R., R. W. Healy, and P. G. Cook (2002b), Choosing appropriate techniques for quantifying groundwater recharge, Hydrogeol. J., 10, 18 – 39.

Scanlon, B. R., K. Keese, R. C. Reedy, J. Simunek, and B. J. Andraski (2003a), Variations in flow and transport in thick desert vadose zones in response to paleoclimatic forcing (0 – 90 kyr): Field measurements, modeling, and uncertainties, Water Resour. Res., 39(7), 1179, doi:10.1029/2002WR001604.

Scanlon, B. R., R. C. Reedy, and K. E. Keese (2003b), Estimation of groundwater recharge in Texas related to aquifer vulnerability to contamination, report, Tex. Comm. on Environ. Qual., Austin.

Schaap, M. G., F. J. Leij, and M. T. van Genuchten (2001), ROSETTA: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions, J. Hydrol., 251, 163 – 176.

Scott, R. L., W. J. Shuttleworth, T. O. Keefer, and A. W. Warrick (2000), Modeling multiyear observations of soil moisture recharge in the semiarid American Southwest, Water Resour. Res., 36, 2233 – 2247.

Sophocleous, M. (1992), Groundwater recharge estimation and regionalization: The Great Bend Prairie of central Kansas and its recharge statistics, J. Hydrol., 137, 113 – 140.

United Nations Environment Programme (1992), World Atlas of Desertification, Edward Arnold, London.

U.S. Department of Agriculture (USDA) (1994), State soil geographic (STATSGO) Data Base, Misc. Publ. 1492, Nat. Resour. Conserv. Serv., Washington, D. C.

U.S. Department of Agriculture (USDA) (1995), Soil Survey Geographic Data Base, SSURGO, Misc. Publ. 1527, Nat. Resour. Conserv. Serv., Washington, D. C.

Vogelmann, J. E., S. M. Howard, L. Yang, C. R. Larson, B. K. Wylie, and N. van Driel (2001), Completion of the 1990s National Land Cover Data set for the conterminous United States from Landsat Thematic Mapper data and ancillary data sources, Photogramm. Eng. Remote Sens., 67, 650 – 662.

Wilcox, B. P. (2002), Shrub control and streamflow on rangelands: A process based viewpoint, J. Range Manage., 55, 318 – 326.

Wood, W. W., and W. E. Sanford (1995), Chemical and isotopic methods for quantifying ground-water recharge in a regional, semiarid environment, Ground Water, 33, 458 – 468.

Zhang, L., W. R. Dawes, and T. J. Hatton (1996), Modeling hydrologic processes using a biophysically based model—Application of WAVES to FIFE and HAPEX-MOBILHY, J. Hydrol., 185, 147 – 169.

Zhang, L., W. R. Dawes, T. J. Hatton, P. H. Reece, G. T. H. Beale, and I. Packer (1999), Estimation of soil moisture and groundwater recharge using the TOPOG_IRM model, Water Resour. Res., 35, 149 – 161.