20221014 复数、双曲复数、对偶数

前言

本博文介绍三种复数形式。

一. 双曲正弦函数和双曲余弦函数

- 双曲正弦函数

$$\sinh x=\frac{e^x-e^{-x}}{2}$$
双曲正弦函数的泰勒展开式为：
$$\sinh x=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\frac{x^7}{7!}+\cdots \cdots$$
即: $\sinh x={\sum }_{n=0}^{\infty }\frac{x^{2n+1}}{(2n+1)!}$

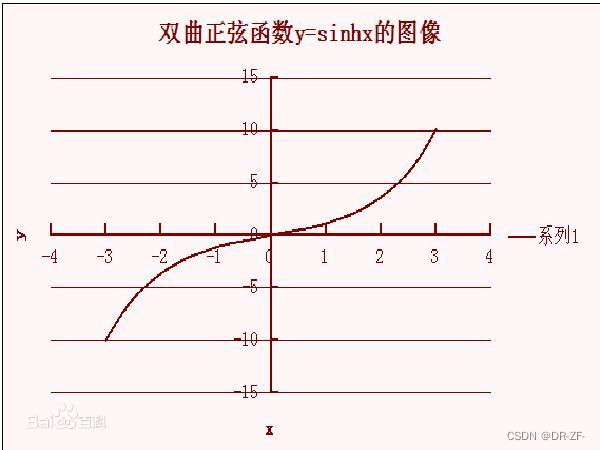
- 双曲余弦函数

$$\cosh x=\frac{e^x+e^{-x}}{2}$$

双曲正弦函数的泰勒展开式为：$$\cosh x=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!}+\cdots$$

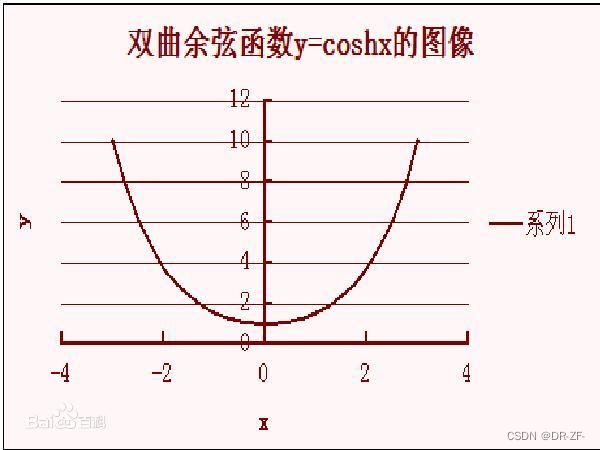
- 双曲正切函数

$$\tanh x=\frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

二. 角度定义

圆角（来源于三角函数、圆函数）：$\alpha$ 对应图形面积的2倍。

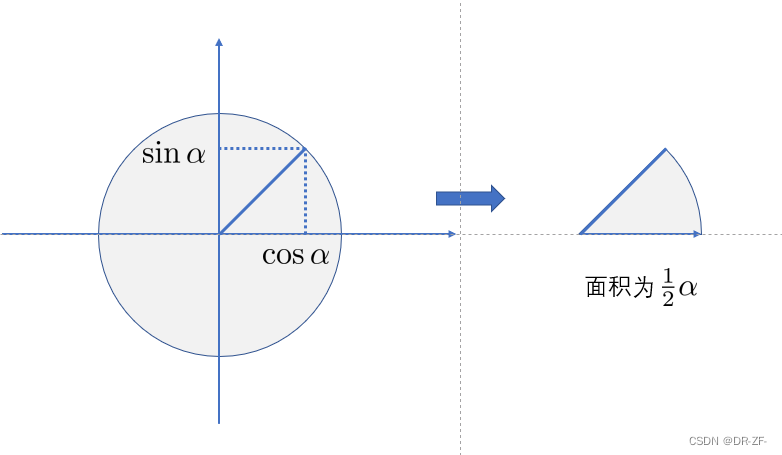
双曲角（来源于双曲函数）：$\alpha$ 对应图形面积的2倍。

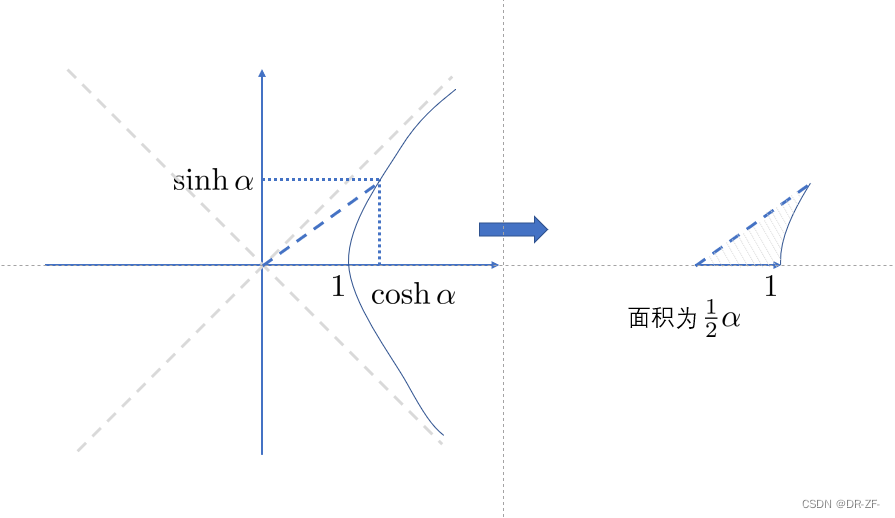
注意：这里并没有说哪个角度是$\alpha$，可以将其理解成关于夹角的某个单调增函数。

右图具体面积等于$\frac{1}{2}ln(x+y)$，根据双曲角的定义$\alpha =\frac{2}{2}ln(x+y)$，即$x+y=\exp (\alpha )$；且$x^2-y^2=1$，则有$x-y=\exp (-\alpha )$，则有$x=\frac{\exp (\alpha )+\exp (-\alpha )}{2}$和$y=\frac{\exp (\alpha )-\exp (-\alpha )}{2}$。

这里非常巧妙的简约形式，来源于一个虚拟的角 $\alpha$，或者说从面积的角度定义了角，这确实打开了新的思路。

三. 复数、双曲复数、对偶数（实数的扩张）

- 单位圆 $x^2+y^2=1$

单位圆上定义复数单位 $i$，对应面积为$\frac{\alpha }{2}$，对应复数为$\cos \alpha +i\sin \alpha$，指数形式 $\exp (i\alpha )=\cos \alpha +i\sin \alpha$，展开为$$\exp (i\alpha )=1+i\alpha +\frac{1}{2!}{i}^2{\alpha }^2+\frac{1}{3!}{i}^3{\alpha }^3+\frac{1}{4!}{i}^4{\alpha }^4+\cdots$$$$\cos \alpha =\sum _{\mathrm{k}=0}^{\infty }\frac{(-1{)}^{\mathrm{k}}}{(2\mathrm{k})!}{\alpha }^{2\mathrm{k}}=1-\frac{1}{2!}{\alpha }^2+\frac{1}{4!}{\alpha }^4-\frac{1}{6!}{\alpha }^6+\cdots$$$$\sin \alpha =\sum _{\mathrm{k}=0}^{\infty }\frac{(-1{)}^{\mathrm{k}}}{(2\mathrm{k}+1)!}{\alpha }^{2\mathrm{k}+1}=\alpha -\frac{1}{3!}{\alpha }^3+\frac{1}{5!}{\alpha }^5-\frac{1}{7!}{\alpha }^7+\cdots$$因此，性质为$i^2=-1$。
同时可知，$a=\sqrt{a^2+b^2}\cos \alpha$，$b=\sqrt{a^2+b^2}\sin \alpha$，那么有$a+ib=\sqrt{a^2+b^2}\cos \alpha +i\sqrt{a^2+b^2}\sin \alpha$，因此缩放为$a+ib=\sqrt{a^2+b^2}\exp (i\alpha )$。

- 单位双曲线 $x^2-y^2=1$

单位双曲线上定义双曲复数单位 $j$，对应面积为$\frac{\alpha }{2}$，对应复数为$\cosh \alpha +j\sinh \alpha$，指数形式 $\exp (j\alpha )=\cosh \alpha +j\sinh \alpha$，根据第1节中的 $\cosh$ 和 $\sinh$ 的展开形式，$$\exp (j\alpha )=1+j\alpha +\frac{1}{2!}{j}^2{\alpha }^2+\frac{1}{3!}{j}^3{\alpha }^3+\frac{1}{4!}{j}^4{\alpha }^4+\cdots$$$$\cosh \alpha =1+\frac{{\alpha }^2}{2!}+\frac{{\alpha }^4}{4!}+\frac{{\alpha }^6}{6!}+\cdots$$$$\sinh \alpha =\alpha +\frac{{\alpha }^3}{3!}+\frac{{\alpha }^5}{5!}+\frac{{\alpha }^7}{7!}+\cdots \cdots$$因此，性质为 $j^2=1$。

同时可知，$$\frac{a}{\cosh \alpha }=\frac{b}{\sinh \alpha }=\frac{\sqrt{a^2-b^2}}{\sqrt{{\cosh }^2\alpha -{\sinh }^2\alpha }}=\sqrt{a^2-b^2},\text{if}a>b,a>0$$考虑其他的三个方向，则有$$a=\sqrt{|a^2-b^2|}\cosh \alpha ，b=\sqrt{|a^2-b^2|}\sinh \alpha$$缩放为$a+jb=\sqrt{|a^2-b^2|}\exp (j\alpha )$。

- 单位双竖线 $x^2=1$

右支上的点定义为$1+ϵ\alpha$，对应面积为$\frac{1}{2}\alpha$，$ϵ$叫对偶数

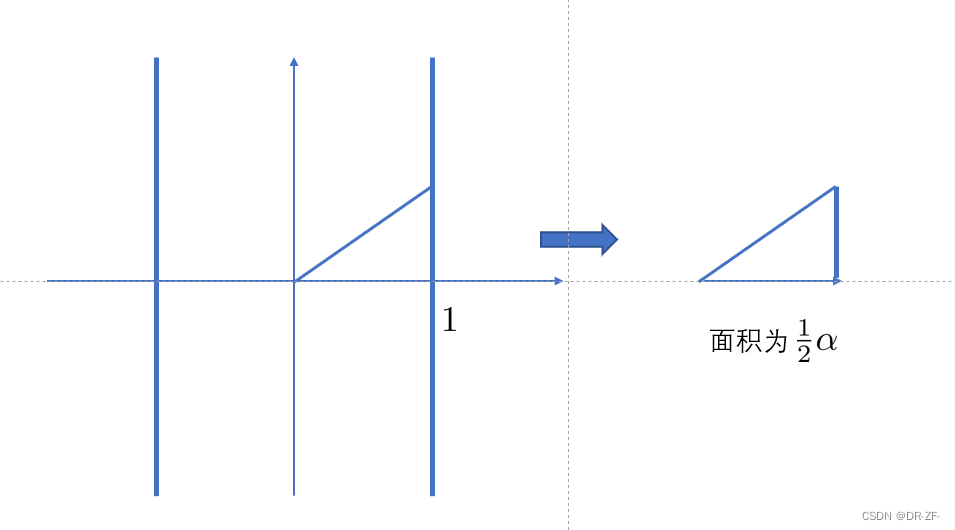
为使其也有相应版本的指数形式，$\exp (ϵ\alpha )=1+ϵ\alpha$，那么相应泰勒展开后说明，一旦${ϵ}^2=0$，上式成立。

那么对偶数的定义为$ϵ\ne 0$且${ϵ}^2=0$。

$ϵ(a+ϵb)=aϵ$，向横坐标投影再逆时针旋转90度

缩放为$a+\epsilon b=|a|\exp (j\alpha )$

- 模：根号下自己乘自己的共轭

为什么在三个图中的模的具体定义不同？这是因为在三张同样的图上，定义的能量函数不同。

注：

参考：Bilibili 风竹云墨
https://www.bilibili.com/video/BV1xp4y1v7cw/?vd_source=5138fcb56aada2b6f1c51dfff686251a

https://baike.baidu.com/item/%E5%8F%8C%E6%9B%B2%E6%AD%A3%E5%BC%A6%E5%87%BD%E6%95%B0/4395524?fromtitle=sinh&fromid=1965202&fr=aladdin

https://zhuanlan.zhihu.com/p/444445404