学习MSCKF笔记——前端、图像金字塔光流、Two Point Ransac

学习MSCKF笔记——前端、图像金字塔光流、Two Point Ransac

前段时间开始工作了，刚开始有点忙得缓不过来，调整了两三个月后总算有时间了，可以继续学点自己感兴趣的东西，写写博客。之前研究过一段时间VINS-Mono，那是一个后端优化框架的VIO，而MSCKF是基于滤波的框架，对于嵌入式平台会更加友好，因此想花点时间再学习下。目前我仅仅看了一遍paper，过了一遍代码，以及学习了几位前辈优秀的博客：
一步步深入了解S-MSCKF
MSCKF那些事（一）MSCKF算法简介
还有深蓝学院吴博的课程，我的这篇博客主要是我自己学习过程中的笔记，参考内容主要如上。

我学习的代码是msckf_vio，代码写得非常简介明了，读代码可以比较容易地总结出前端算法的流程图如下：

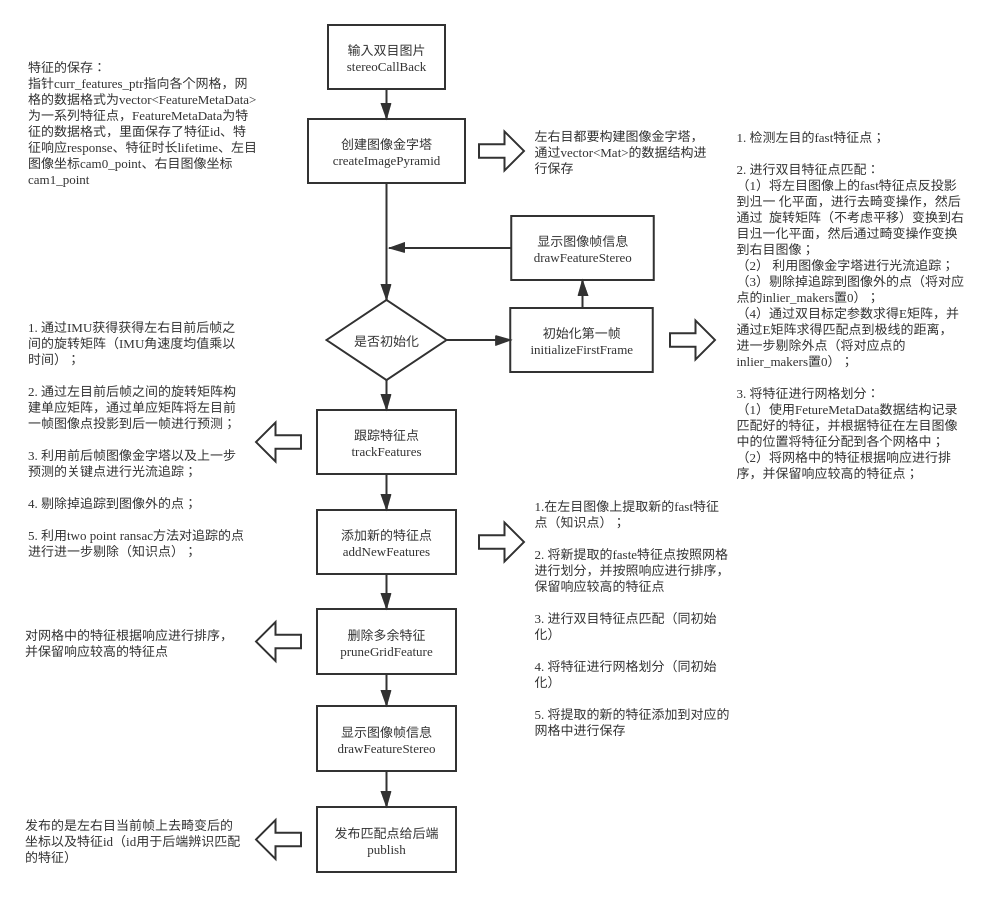
这里我主要对代码中的几个细节进行简单分析，包括图像金字塔光流、Two Point Ransac算法、新Fast特征点提取

1. 图像金字塔光流

光流法我们再熟悉不过了，MSCKF为了节省计算量，在图像输入时就对图像进行了金字塔操作，那么金字塔光流是如何实现的，收益是怎样的，下面先对金字塔光流进行推导。金字塔光流的参考论文为Pyramidal Implementation of the Lucas Kanade Feature Tracker Description of the algorithm.

我们知道光流法最基本的原理如下：$$I(x+\Delta x,y+\Delta y,t+\Delta t)-I(x,y,t)=\frac{\partial I}{\partial x}\Delta x+\frac{\partial I}{\partial y}\Delta y+\frac{\partial I}{\partial t}\Delta t$$当$\Delta t$足够小时，有$$-\frac{\partial I}{\partial t}=\frac{\partial I}{\partial x}\frac{dx}{dt}+\frac{\partial I}{\partial y}\frac{dy}{dt}=\frac{\partial I}{\partial x}u+\frac{\partial I}{\partial y}v$$即$$-I_t=\left[\begin{array}{ll}{I}_x& I_y\end{array}\right]\left[\begin{array}{l}u\\ v\end{array}\right]$$其中$I_x,I_y$为像素梯度，$u,v$为像素运动速度，是我们要求的未知量。一个约束方程无法求解二元方程，因此就诞生Lucas-Kanade光流，假定邻域像素具备运动一致性，取邻域像素进计算求解：$$\{\begin{array}{l}{I}_{1x}u+I_{1y}v=-I_{1t}\\ I_{2x}u+I_{2y}v=-I_{2t}\\ \cdots \\ I_{nx}u+I_{ny}v=-I_n\end{array}$$令$$\mathbf{A}=\left[\begin{array}{c}{\left[I_x,I_y\right]}_1\\ ⋮\\ {\left[I_x,I_y\right]}_k\end{array}\right],\mathbf{b}=\left[\begin{array}{c}{I}_{t1}\\ ⋮\\ I_{tk}\end{array}\right]$$于是有$${\left[\begin{array}{c}u\\ v\end{array}\right]}^{\ast }=-{\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\mathbf{b}$$由于Lucas-Kanada光流取的是邻域像素，如果像素运动过快超出邻域就无法满足以上假设了，因此就诞生了金字塔光流法：使用低分辨率的图片来估计高分辨率图片像素的运动趋势。
首先是构建高斯金字塔，所谓高斯金字塔就是通过高斯下采样构建的，如下图所示：

高斯下采样可以理解为先进行高斯模糊，再进行下采样的操作，通过高斯下采样图像尺寸为原尺寸的一半，原始图片在最底层（第0层），分辨率最低的图片在最顶层（第$L_m$层）。我们假设第$L$层的光流的估计的某个像素的位移为$g^L$（估计值），那么第$L-1$层的光流估计的该像素的位移为:$$g^{L-1}=2(g^L+d^L)$$其中$d^L$为根据第$L-1$层图像求得的修正量（修正值），具体的推到过程如下所示：
我们首先定义第$L$层像素邻域范围内的匹配误差和如下：$${ϵ}^L\left(d^L\right)={ϵ}^L\left(d_x^L,d_y^L\right)=\sum _{x=u_x^L-{\omega }_x}^{u_x^L+{\omega }_x}\sum _{y=u_y^L-{\omega }_y}^{u_v^L+{\omega }_y}{\left(I^L(x,y)-J^L\left(x+g_x^L+d_x^L,y+g_y^L+d_y^L\right)\right)}^2$$其中，$I$和$J$是前后两帧不同的图像，$g_x^L,g_y^L$是由上一层光流的估计值（$g_x^L=2(d_x^{L+1}+d_x^{L+1}),g_y^L=2(g_x^{L+1}+d_y^{L+1})$），$d_x^L,d_y^L$为当前层我们要求的的修正值。且我们假设最顶层（第$L_m$层）的光流估计的估计值为$$g^{L_m}={\left[\begin{array}{ll}0& 0\end{array}\right]}^T$$接下来为了推到的方便，我们对上面的匹配误差和损失函数进行重写，令$$\forall (x,y)\in \left[p_x-{\omega }_x-1,p_x+{\omega }_x+1\right]\times \left[p_y-{\omega }_y-1,p_y+{\omega }_y+1\right]，A(x,y)\doteq I^L(x,y)$$$$\forall (x,y)\in \left[p_x-{\omega }_x,p_x+{\omega }_x\right]\times \left[p_y-{\omega }_y,p_y+{\omega }_y\right]，B(x,y)\doteq J^L\left(x+g_x^L,y+g_y^L\right)$$$$\overline{\nu }={\left[{\nu }_x,{\nu }_y\right]}^T={\mathrm{d}}^L$$那么我们要求的损失函数可以写为：$$\epsilon (\bar{\nu })=\epsilon \left({\nu }_x,{\nu }_y\right)=\sum _{x=p_x-{\omega }_x}^{p_x+{\omega }_x}\sum _{y=p_y-{\omega }_y}^{p_y+{\omega }_y}{\left(A(x,y)-B\left(x+{\nu }_x,y+{\nu }_y\right)\right)}^2$$为了最小化损失函数，我们对损失函数进行求导：$$\frac{\partial \epsilon (\bar{\nu })}{\partial \bar{\nu }}=-2\sum _{x=p_x-{\omega }_x}^{p_x+{\omega }_x}\sum _{y=p_y-{\omega }_y}^{p_y+{\omega }_y}\left(A(x,y)-B\left(x+{\nu }_x,y+{\nu }_y\right)\right)\cdot \left[\begin{array}{cc}\frac{\partial B}{\partial x}& \frac{\partial B}{\partial y}\end{array}\right]$$然后我们对$B\left(x+{\nu }_x,y+{\nu }_y\right)$进行泰勒展开，有：$$\frac{\partial \epsilon (\bar{\nu })}{\partial \bar{\nu }}\approx -2\sum _{x=p_x-{\omega }_x}^{p_x+{\omega }_x}\sum _{y=p_y-{\omega }_y}^{p_y+{\omega }_y}\left(A(x,y)-B(x,y)-\left[\begin{array}{cc}\frac{\partial B}{\partial x}& \frac{\partial B}{\partial y}\end{array}\right]\bar{\nu }\right)\cdot \left[\begin{array}{cc}\frac{\partial B}{\partial x}& \frac{\partial B}{\partial y}\end{array}\right]$$接下来，我们令：$$\delta I(x,y)\doteq A(x,y)-B(x,y)$$$$\nabla I=\left[\begin{array}{l}{I}_x\\ I_y\end{array}\right]\doteq {\left[\begin{array}{cc}\frac{\partial B}{\partial x}& \frac{\partial B}{\partial y}\end{array}\right]}^T$$其中$$I_x(x,y)=\frac{\partial A(x,y)}{\partial x}=\frac{A(x+1,y)-A(x-1,y)}{2}$$$$I_y(x,y)=\frac{\partial A(x,y)}{\partial y}=\frac{A(x,y+1)-A(x,y-1)}{2}$$
因此有$$\frac{1}{2}\frac{\partial \epsilon (\bar{\nu })}{\partial \bar{\nu }}\approx \sum _{x=p_x-{\omega }_x}^{p_x+{\omega }_x}\sum _{y=p_y-{\omega }_y}^{p_y+{\omega }_y}\left(\nabla I^T\bar{\nu }-\delta I\right)\nabla I^T$$将具体参数代入得：$$\frac{1}{2}{\left[\frac{\partial \epsilon (\bar{\nu })}{\partial \bar{\nu }}\right]}^T\approx \sum _{x=p_x-{\omega }_x}^{p_x+{\omega }_x}\sum _{y=p_y-{\omega }_y}^{p_y+{\omega }_y}\left(\left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right]\bar{\nu }-\left[\begin{array}{c}\delta I{I}_x\\ \delta I{I}_y\end{array}\right]\right)$$令$$G\doteq \sum _{x=p_x-{\omega }_x}^{p_x+{\omega }_x}\sum _{y=p_y-{\omega }_y}^{p_y+{\omega }_y}\left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right]$$$$\bar{b}\doteq \sum _{x=p_x-{\omega }_x}^{p_x+{\omega }_x}\sum _{y=p_y-{\omega }_y}^{p_y+{\omega }_y}\left[\begin{array}{c}\delta I{I}_x\\ \delta I{I}_y\end{array}\right]$$
则有$$\frac{1}{2}{\left[\frac{\partial \epsilon (\bar{\nu })}{\partial \bar{\nu }}\right]}^T\approx G\bar{\nu }-\bar{b}$$那我们最终要求的$\bar{\nu }$为：$$\bar{\nu }=G^{-1}\bar{b}$$这实际上就是求出了第$L$层图像的修正量$d^L$，结合估计值$g^L$就可以求出来下一层的估计值$g^{L-1}$，直到求导最底层，也就是我们原始图片的估计值。

2. Two Point Ransac算法

Two Point Ransac算是是原文作者提出来的一个新算法，算法的目的时在前后帧跟踪特征点时是筛选出前后帧匹配的outliers，在执行Two Point Ransac之前，先对当前帧追踪到的特征点进行双目匹配，去除掉一部分不满足双目极限约束的特征点。可以看到，虽然用的是双目相机，但是只对左目使用了光流法进行特征追踪，因此接下来的Two Point Ransac是对左右目共同使用的。

Two Point Ransc的流程是先通过IMU角速度均值乘以时间获得的前后帧旋转矩阵$R$，然后通过旋转矩阵$R$将上一帧的特征点投影到当前帧，这时上一帧的特征点和当前帧匹配的特征点之间就差一个平移$t$，用公式描述如下：
首先前后两帧之间的匹配点满足极线约束：$$p_2^T\cdot [t{]}_x\cdot R\cdot p_1=0$$，通过旋转矩阵$R$将前一帧特征点投影到当前帧之后坐标分别为：$$R\cdot p_1={\left[\begin{array}{lll}x1& y1& 1\end{array}\right]}^T,p_2={\left[\begin{array}{lll}x2& y2& 1\end{array}\right]}^T$$，那么满足$$\left[\begin{array}{ccc}{x}_2& y_2& 1\end{array}\right]\cdot \left[\begin{array}{ccc}0& -t_z& t_y\\ t_z& 0& -t_x\\ -t_y& t_x& 0\end{array}\right]\cdot \left[\begin{array}{c}{x}_1\\ y_1\\ 1\end{array}\right]=0$$对其进行展开后$$\left[\begin{array}{lll}{y}_1-y_2& -\left(x_1-x_2\right)& x_1{y}_2-x_2{y}_2\end{array}\right]\cdot \left[\begin{array}{l}{t}_x\\ t_y\\ t_z\end{array}\right]=0$$由于误差的存在，并不是所有匹配的特征点都会满足上面的等式，我们考虑两个点的情况有：$$\left[\begin{array}{ccc}{y}_1-y_2& -\left(x_1-x_2\right)& x_1{y}_2-x_2{y}_2\\ y_3-y_4& -\left(x_3-x_4\right)& x_3{y}_4-x_4{y}_3\end{array}\right]\cdot \left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]={\left[\begin{array}{c}{A}_x\\ A_y\\ A_z\end{array}\right]}^T\cdot \left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]\approx \left[\begin{array}{l}0\\ 0\end{array}\right]$$平移向量有三个变量，两个点是无法求解的，因此将上面的式子拆解成如下三个式子：$$\begin{array}{l}{\left[\begin{array}{c}{A}_x\\ A_y\end{array}\right]}^T\cdot \left[\begin{array}{l}{t}_x\\ t_y\end{array}\right]\approx A_z\cdot t_z\\ {\left[\begin{array}{c}{A}_x\\ A_z\end{array}\right]}^T\cdot \left[\begin{array}{c}{t}_x\\ t_z\end{array}\right]\approx A_y\cdot t_y\\ {\left[\begin{array}{c}{A}_y\\ A_z\end{array}\right]}^T\cdot \left[\begin{array}{c}{t}_y\\ t_z\end{array}\right]\approx A_x\cdot t_x\end{array}$$并添加尺度约束$$\begin{array}{rl}& \{\begin{array}{l}\text{ if }{t}_x<t_y\&\&t_x<t_z,\text{ then }{t}_x=1\\ \left[-\left(x-x^{\prime }\right),\left(x{y}^{\prime }-x^{\prime }y\right)\right]\left[\begin{array}{c}{t}_y\\ t_z\end{array}\right]=-\left(y-y^{\prime }\right)\end{array}\\ & \{\begin{array}{l}\text{ if }{t}_y<t_x\&\&t_y<t_z,\text{ then }{t}_y=1\\ \left[\left(y-y^{\prime }\right),\left(x{y}^{\prime }-x^{\prime }y\right)\right]\left[\begin{array}{c}{t}_x\\ t_z\end{array}\right]=\left(x-x^{\prime }\right)\end{array}\\ & \{\begin{array}{l}\text{ if }{t}_z<t_x\&\&t_z<t_y,\text{ then }{t}_z=1\\ \left[\left(y-y^{\prime }\right),-\left(x-x^{\prime }\right)\right]\left[\begin{array}{c}{t}_x\\ t_y\end{array}\right]=-\left(x{y}^{\prime }-x^{\prime }y\right)\end{array}\end{array}$$
根据上面三个中的任意一个，我们就可以求出平移向量$t$，根据求解平移向量$t$我们求得各对匹配的特征点之间的误差，根据误差大小设定阈值就可以判断哪些特征点是outliers，哪些点是inliers，接下来我们整理下完整的RANSAC算法的流程：
（1）先从前后帧所有匹配点中随机选取两对匹配点进行上面的计算，获得平移向量$t$；
（2）通过平移向量$t$计算其他所有匹配点的误差，根据误差判定哪些是inlers，哪些是outliers；
（3）根据所有的inlers重新求得平移向量$t$；
（4）根据新的平移向量$t$计算所有匹配点的误差，若误差和小于之前RANSAC采样获得的最小误差，则将inliers和误差记录下来
（5）最终输出误差最小的inlers组合。
最后补一句，RANSC的迭代次数由用户需求的成功率和inlers比例确定，计算公式如下：$$M=\frac{\log \left(1-p_s\right)}{\log \left(1-p^K\right)}$$其中$p_s$为RANSC成功率，$p$为inlers比例

3. 新特征点提取

新特征点提取过程中，为了保证提取的有效性，MSCKF采用了两种手段：
（1）在提取特征点是使用的Mask操作，这个操作在VINS-Mone中也使用了，不过VINS-Mono中使用的圆形，MSCKF中使用的是方形，这个可以参考我之前写过的博客：VINS-Mono关键知识点总结——前端详解，加不加Mask提取的特征点的效果会有很大差别的。
（2）就是将特征点分配到网格中进行管理，并根据响应进行排序，删除掉响应低的特征点，这样做可以提高特征点的有效性。

以上就是我学习前端时的一些关注点，因为也是在学习，难免会有理解不对的地方，如果有问题欢迎指出欢迎交流～下个礼拜写后端

此外，对其他SLAM算法感兴趣的同学可以看考我的博客SLAM算法总结——经典SLAM算法框架总结