分枝定界图解（含 Real-Time Loop Closure in 2D LIDAR SLAM论文部分解读及BB代码部分解读）

分枝定界图解

网上对分枝定界的解读很多都是根据这篇必不可少的论文《Real-Time Loop Closure in 2D LIDAR SLAM》来的。

分枝定界是一种深度优先的树形搜索方法，避免了暴力搜索带来的计算量庞大等问题，成为cartographer的重要组成部分。

其很好地被用于激光slam的回环检测中。用当前的scan和全局地图global map进行匹配，以找到此帧scan的位姿。

所以目的要明确——寻找当前帧的位姿。

下面就开始分枝定界的图解。希望读者同论文一起解读。

---

参考：

论文：Real-Time Loop Closure in 2D LIDAR SLAM

论文翻译：https://blog.csdn.net/luohuiwu/article/details/88890307

论文解读：https://blog.csdn.net/weixin_36976685/article/details/84994701

栅格地图：https://zhuanlan.zhihu.com/p/21738718

---

1.栅格地图

首先需要明确，什么是栅格地图，或者叫占据栅格地图。

https://zhuanlan.zhihu.com/p/21738718

建议读者仔细阅读上述链接。当然，可以先接着往下看。我这里总结一下上述链接的内容。

我们将地图划分成细小的栅格，每一个栅格可以用栅格中心点（grid point）表示。每一个栅格都有两个状态：

（1）free 未被占据
（2）occupied 被占据

现实中我们知道，一个栅格被占据或者不被占据都是可以直接感知到的。比如我们拿肉眼跑过去看，哪个地方被占据，哪个地方没被占据，都是确定的。但是如果我们用传感器（激光雷达）去感知这个世界，一切仿佛并没有那么确定，这是因为一个东西的存在——测量噪声（或者说测量误差）。

因此，我们没法准确得知道一个栅格的真正状态，有可能它被占据了，但是没测出来；或是它没被占据，但传感器误认为它被占据了。那么不确定问题用什么表述呢？——

概率。

现在我们将每一个栅格赋予一个概率P表示它被占据了。P=0.6，则表示这个栅格有超过一半的概率（0.6）可能被占据。

但事实上为了计算方便等原因，我们对概率值取对数，得到一个量Odd来表示这个栅格被占据的状态。Odd越大，表示这个栅格越可能已经被占据。当然，详细的从P转换为Odd的过程请见上面的链接。

现在，激光雷达的感知过程就转变为不断更新每个栅格的Odd的过程。每一帧激光数据进来，都会更新一次每个栅格的Odd。这个过程包含着贝叶斯的思想。

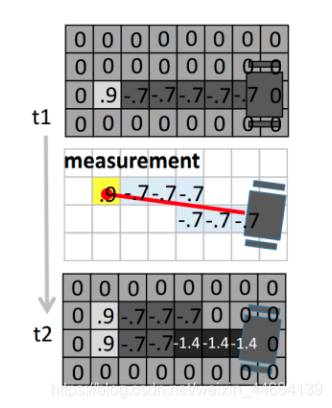
上图可以看出，在激光扫描之前和之后，一些被扫描到的栅格的Odd的更新。

至此，你可能大致明白栅格地图是什么东西了。他是一个似然场，每一个栅格都有属于自己的状态。

最后，栅格可以用一个栅格点（grid point）代替，有时候可能更便于理解。这一个栅格可以被叫做一个“像素（pixel）”，其边长一般称为r，即为像素宽。

用论文中的图表示的话就是：

中间的叉叉表示grid point，栅格点间距离即为像素宽r

2.回环检测

回环检测的目的是，通过当前扫描帧scan的数据，与global map全局的地图进行匹配，得到当前的scan的位姿。（也就是搭载激光雷达的机器人的位姿）

这里用个简图表示，不再多说。（因为既然想知道分枝定界，相信你回环检测的概念肯定已经很清楚了）

黄色代表此帧机器人坐标系下的激光数据，蓝色代表全局地图中的激光点。当然，真实情况肯定不只是这几个点。我们尝试找到一个位姿T（二维问题中，T为(x, y, θ)），能够使得将黄色的点映射到地图坐标系中，能够尽可能的接近甚至重合于地图点。比如上图中，框内的点是经过旋转关系可以进行对应的。

那么事实上，我们说过我们将真实的世界划分为栅格。而栅格是有概率的，或者说是状态值odd的。那么我们就想找到一个位姿T，使得将激光点数据映射到全局地图中，能够有足够大的概率——即地图坐标系中所有激光点所在的所有栅格的Odd之和足够大，这样就意味着回环上了。

回环上的意思就是——我们通过这一帧scan的数据和全局地图的匹配，找到了属于这个scan的位姿。

那也有可能没回环上，也就是说，找不到能特别好匹配上全局地图的位姿，那么则没有构成回环。

那么如何找到这个位姿T呢？

2020.5.17校正–如果你只是为了理解分枝定界，继续往下阅读即可。如果你对源代码是如何操作的感兴趣，那么可以看看我的说法校正（因为写这篇文章的时候还没有看源代码）

其实在源代码中，回环上的意思是，找到一个节点node，找到一个子图submap。首先这个node和这个submap本身就不一定在同一条轨迹当中，当然也可能在同一条轨迹当中。他俩如果离得不算太远，那么就有回环的潜质。

此时，先找到node相对于submap的相对位姿，即这个node在这个子图中的位姿。然后再在这个node附近进行位姿搜索，找到一个最佳的匹配，从而构成回环。

源代码整体脉络：https://blog.csdn.net/weixin_44684139/article/details/105947152

3.暴力搜索

一个很直观的思想，我们进行暴力搜索。暴力搜索肯定要确定一个搜索范围，在搜索范围内遍历。

之前说过，T是（x,y,θ）。

根据里程计等等方法，你可以大致知道这个时刻scan的位姿大约是多少，只不过有累计误差，但也偏的不会太多太多。因此我们考虑，在这个有误差的位姿附近搜索即可。假设这个包含累积误差的初始“预估位姿”为ξ0，那么我们在它的四周布置一个搜索框。如14m边长的正方形。（这里把位姿叫做ξ，不叫做T，是为了和论文保持一致的叫法）

请注意，这里的搜索框，是抽象出来的，数学层面的搜索，可以不理解为真实世界中放置的搜索框。也千万不要理解为栅格地图。

（原谅我画的不均匀。。。。。初始位姿ξ0应该是在搜索框正中心的，搜索框边长是14m）

其中的每一个小格的边长代表了此搜索框的分辨率。可能是5cm呀，50cm呀，都有可能。

接下来就是在这个搜索框中暴力搜索。每一个交点代表一个（x, y），对于每个交点，又有一组θ需要遍历。因此就是三层for循环：
for x
----for y
------for θ
当然，我们知道计算三角函数是更耗时的。因此为了一定程度减小计算量，可以
for θ
----for x
------for y

如何知道遍历的哪个位姿是最符合要求的、我们想要的、回环的位姿呢？

这就需要一个评分机制。

对于每一个遍历出来的(x, y, θ)，我们给它打个分。分最高的我们认为是回环上的位姿。

那么如何进行评分呢？

4.评分机制

我们要在所有遍历的位姿中，找到得分最高的那个。按照论文中的写法是：

其中W为搜索范围，K表示当前的scan有K个激光点，T表示位姿。M表示什么呢？也许式子晦涩难懂。这里我们看图说话。

我们画出以下栅格地图。注意，这里不是画的搜索框哦。

假设当前scan帧就打出两个激光点（当然，实际上一帧激光有好上百个点，这里是为了简化计算过程），一个橙色的，一个蓝色的，并且我们通过当前遍历到的(x1, y1, θ1)将激光点映射到全局地图坐标系中（如上图）

我们知道，地图是用占据栅格表述的。每个栅格有自己的状态，称为Odd。

蓝色的点落入的栅格，它的Odd为0.7，橙色点所在栅格Odd为0.2。之前说过，Odd越大，表示越有可能被占据。

接下来进行打分： score(当前遍历的(x1, y1, θ1)) = 0.2 + 0.7 = 0.9

至于公式中的M nearest(), 表示的就是每个激光点的小分（0.2或是0.7）是：用与他最近的地图点(grid point)的状态量表示。也就是激光点所在栅格的状态量。随你怎么叫。

下面开始遍历第二个，(x2, y2, θ2)，用这个位姿将激光点投影到地图坐标系下。

接下来进行打分： score(当前遍历的(x2, y2, θ2)) = 0.5 + 0.9 = 1.4

为了以后讲解，我将这种打分规则称为：平凡打分法

则我们认为，(x2, y2, θ2)比(x1, y1, θ1)更有可能是正确的姿态。

这样，一个个(x, y, θ)不断遍历，直至遍历完毕，找到一个得分最高的，就是我们认为的回环解。也就是当前scan的匹配位姿，是我们需要的最优解。

我们可以看到，暴力求解是有庞大的计算量的。因为你要把搜索框（search window）中的位姿以分辨率为步长全部遍历一遍。

原论文给出了暴力求解的伪代码，因为建议本blog和论文一起食用效果最佳，所以看到这里，伪代码应该也会很明白了。无非就是三层for循环。

4.分枝定界

因为要做到实时闭环检测，计算量如此之大。所以肯定不可取。

因此，2016年的论文《Real-Time Loop Closure in 2D LIDAR SLAM》使用了一种能够大大减少计算量，并能够不遗漏最优解的方法——分枝定界。（相对于多分辨率搜索而言的，但是这里不讲多分辨率搜索，因为他被分枝定界暴打）

分枝定界（或称分支限界、分枝上界）是什么意思呢？

以下为引用--------------------------------------------------------------------------------------------------------

分枝界限法是由三栖学者查理德·卡普（Richard M.Karp）在20世纪60年代发明，成功求解含有65个城市的旅行商问题，创当时的记录。“分枝界限法”把问题的可行解展开如树的分枝，再经由各个分枝中寻找最佳解。

其主要思想：把全部可行的解空间不断分割为越来越小的子集（称为分支），并为每个子集内的解的值计算一个下界或上界（称为定界）。在每次分支后，对凡是界限超出已知可行解值那些子集不再做进一步分支。这样，解的许多子集（即搜索树上的许多结点）就可以不予考虑了，从而缩小了搜索范围。

以上为引用--------------------------------------------------------------------------------------------------------

分枝定界是一种深度优先的树搜索算法。通过对树进行剪枝，可以缩小了搜索范围，大大减小计算量。但同时又不会遗漏最优解。

请现在就记住，分枝定界思想，就是不断缩小搜索范围的过程。

先让我们认识以下所谓的 “树” 是什么样子：

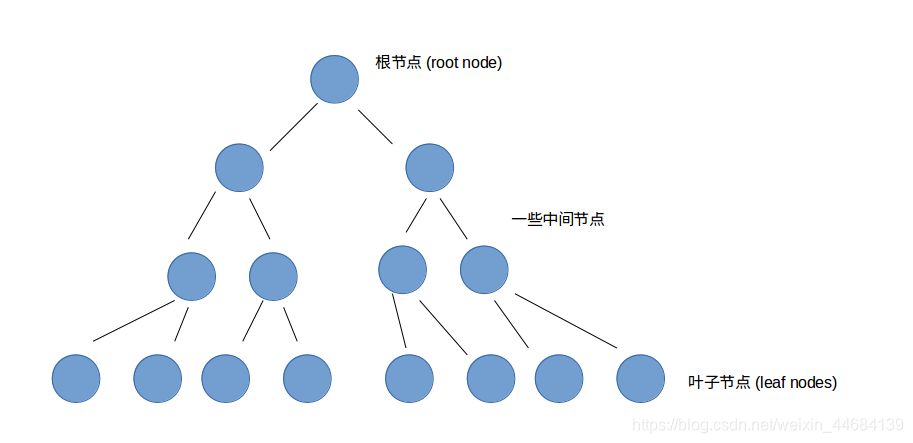
上图是一个简单的高度3(自下而上每层高度分别为0,1,2,3)的二叉树结构。自上而下，从根节点（root node）开始，每个节点被细分为两个子节点，直至不能再被划分的时候，也就是最后一层，height=0。在分枝定界问题中，什么情况下不能再分了呢？——到达了搜索框的最细分辨率则不能再分，也就是在暴力搜索中，那些所有的交点的集合构成了树的叶子节点。

也就是说，回环检测的最优位姿，一定出现在叶子节点。

听不懂的话，继续往下看。

这里我不想囿于论文，只想把东西说清楚。最后我会补充关于论文里面数学理论的一些解释。

如何将树结构应用于搜索最优位姿中呢？它是怎么体现于分枝定界方法呢？

把之前暴力求解的搜索框拿来瞅瞅：（再次强调，这里不是栅格地图了哦）

密密麻麻的搜索框很不合自己那追求简单的心灵。（实际上是密集恐惧症。。。。）

搜索范围太大，步长又太小，太密集了。

下面开始分枝定界（请不要忘记，分枝定界就是不断地缩小搜索范围的过程）

首先定义一个最佳得分best_score = 0.9 ， 这个是初始化的最佳得分，随便设了一个。有什么用呢？以后再说。

将搜索范围重新划分，这时候步长选的大一点，分出来粗一些，考虑到论文中的情况，我这样分。

以左上角为原点，分成四份。原点即为树的根节点，也就是位姿（x0, y0）。这里暂不考虑角度，因为每次进行分枝定界之前都要规定一个角度，这个角度下的分枝定界做完以后，再以一定步长更新换角度，重新开始分枝定界，也就是说，每一次分枝定界的过程中，角度θ是不变的。

通过这一次粗分辨率的分割，我们得到了四个子节点（红色。注意自己也算是自己的子节点）：

这四个子节点分别为（x0, y0），（x0, y1），（x1, y0），（x1, y1）

位姿也就是（x0, y0, θ），（x0, y1, θ），（x1, y0, θ），（x1, y1, θ）。

从代码（代码解读在最后面）中也可以清楚的看到，一个父节点是向右下角的四个子节点进行分枝的

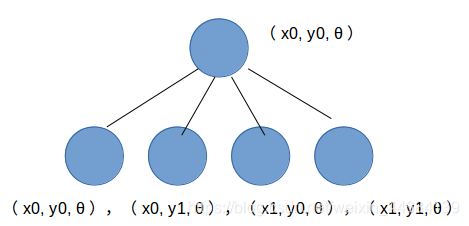
接下来，用这四个位姿，将当前帧scan激光点投影到地图坐标系，跟之前一样，需要根据评分规则进行打分。

但这里的打分规则有所不同。不再是平凡打分法。

这里的打分规则与之前的有什么不一样呢？

注意，这里我们对每一个激光点，用子节点均进行位姿转换。这样激光点会落入栅格地图的某个区域内。之前我们是直接根据其落入的栅格概率进行打分，但现在不是。我们以激光点落入的栅格为起点，向右下角延展4^d个栅格（边长为2^d）

其中d为打分节点所在层数。从下往上为d = 0,1,2,…

然后我们以这个延伸区域中所有栅格中的最大栅格概率作为这个激光点的打分。

不明白没关系，看图说话。

ps：注意这里是栅格地图哦，不是搜索范围。还是之前的橙色和蓝色两个激光点。

对于橙色和蓝色激光点，我们将其通过子节点位姿（x0, y0, θ）进行位姿变换，变换到了栅格地图坐标中：

接下来进行区域延展，以蓝色激光点所在栅格为例进行延展——假如现在处于从下往上数第2层，即d=1: 则需要扩展边长为2的区域：

则取延伸区域中最大分数——蓝色激光点打分为1.1

我将这种打分方法称为——贪心打分法（因为每个激光点都要取区域中最大的栅格概率，太贪心了）

这样，新分出来的四个子节点（x0, y0, θ），（x0, y1, θ），（x1, y0, θ），（x1, y1, θ）都可以得到自己的分数。

假如他们的得分分别为：1.6,1.7,0.2,0.5

还记得我们曾经初始化了一个最佳得分best_score = 0.9吗？好，0.2 和 0.5 这两个节点的分数小于best_score，那么直接将此节点统领的区域全部删除，体现在树上，就是进行了剪枝，将这个父节点的子树全部减掉。

下面这个图体现了剪枝的效果。注意，这是位姿搜索框，而不是栅格地图。

依次类推。直到搜寻至叶子节点，找到叶子节点中的best_score，将具有此best_score的叶子节点的位姿，认为是分枝定界最优解。

这位博主介绍的计算流程为：
（参考blog，改了几个字:https://blog.csdn.net/weixin_36976685/article/details/84994701）

以下为引用--------------------------------------------------------------------------------------------------------

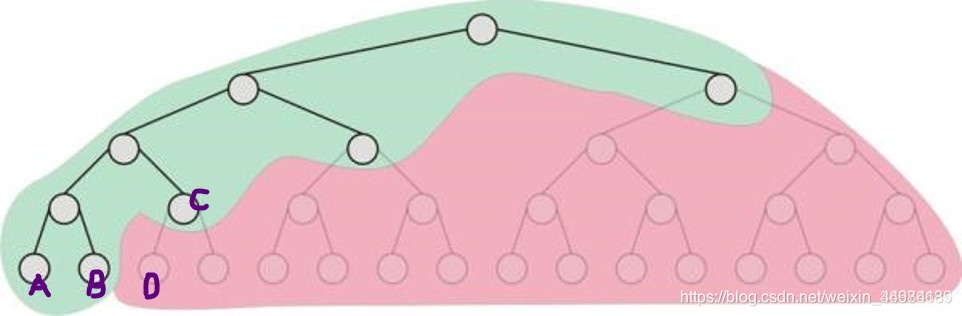
再来看这张图假设我们需要去计算检测匹配的点为如图所示16个
则我们第一层搜索精度最低，只列举其中两个，并优先考虑靠左（优先考虑可能性最高的）。
对其继续分层，将其精度提高一倍，又可以列举出两个，并优先考虑靠左。
这样直至最底层，计算出该情况下的平凡得分，最左的底层有两个值A和B，我们求出最大值，并将其视为best_score
然后我们返回上一层还未来得及展开的C，计算C的贪心得分并让它与best_score比较，若best_score依旧最大，则不再考虑C，即不对其进行分层讨论。
若C的贪心得分比best_score更大，则对其进行分层，计算D和E的值，我们假设D值大于E，则将D与best_score对比
若D最大，则将D视为best_score，否则继续返回搜索。

以上为引用--------------------------------------------------------------------------------------------------------

上面是一种可能性的计算流程。后面的第五部分，我会根据伪代码介绍计算流程。

那么你现在肯定迫不及待得想知道：

为什么要这样给父节点打分呢？

这是为了保证，父节点用贪心打分法的得分永远大于子节点贪心打分法的得分。从而保证，一旦父节点的贪心得分小于best_score，那么这个父节点的子树全部被剪枝，因为其子树的叶子节点的得分肯定小于上面每一层中间节点的贪心得分，所以肯定小于best_score。——递归的思想

贪心打分法的精髓在于：由于一个父节点的子节点永远是在父节点的基础上向右下方移动，也就是之前所说的，扩展子节点是向右下角四个方向进行扩展。那么父节点位姿变换到栅格坐标系中的点云，经过向右下角平移就可以得到子节点的点云。那么我取所有激光点右下角区域中的最大占据概率得分之和，一定比子节点的所有激光点所在栅格的占据概率得分之和要大。

论文中的公式为：（最大值之和 大于 和的最大值）当然，看不懂这个晦涩式子没有关系，能理解分枝定界足以。

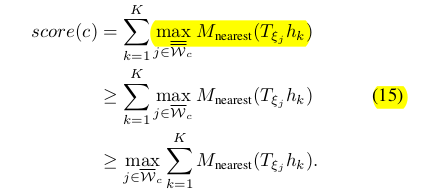
再总结一下剪枝的原则是：如果子树的父节点的贪心score小于之前已经待定的best_score，那么直接将这个节点的子树全部减掉。best_score首次搜索至叶子节点之前，是设定的一个初始值（比如之前设置的0.9）。当第一次搜索到叶子节点之后，若叶子节点的得分高于best_score，best_score会被更新。

以上的解释，你是否已经明白，“定界”的含义了呢？

5.论文的伪代码

论文的算法二给出了简单形式的伪代码。算法三则给出了优化后的伪代码。

下面我们通过树的感觉，真正体会一下这个伪代码的流程。为了计算和解释方便，暂时不像论文中每次分出来四个子节点，这里我们用二叉树。

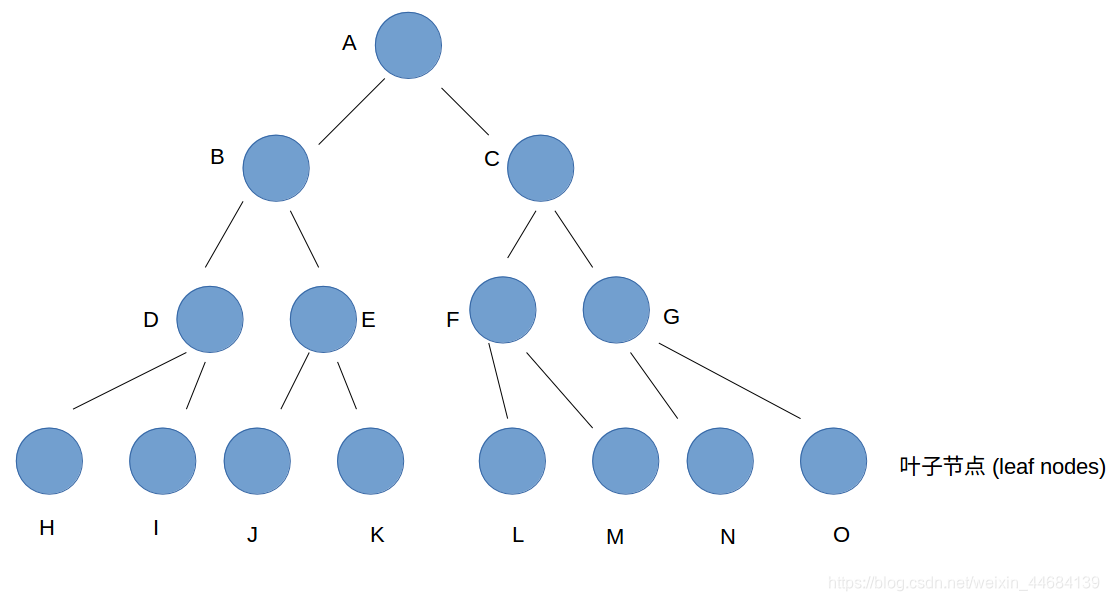
我给每个节点都标上了序号A-----O

A为根节点，H------O为叶子节点，其余为中间节点。

之前的分析有些问题，这不是真正代码中分枝定界的流程。看完代码后，真正体会一下流程：

2020.5.17校正–

（1）先把A(1.5)分为 B(0.9) 和 C(0.8)
（2）先瞅准B(0.9)，将其分为D(0.7)和E(0.2)
（3）再瞅准D(0.7)，将其分为H(0.5)和I(0.4)
（4）得到了最大的叶子节点H(0.5)，得到best(0.5)
（5）返回上一层看E(0.2)，发现E(0.2) < best(0.5)，直接将E及其子树JK剪枝，不再进行循环
（6）继续往上一层返回，看C(0.8)，发现best(0.5)<C(0.8)，则对C(0.8)继续向下分
（7）将C(0.8)分为F(0.4)和G(0.7)
（8）瞅准F(0.4)，发现其小于best(0.5)，则将F及其子树LM进行剪枝
（9）再看G(0.7)，发现其大于best(0.5)，将G(0.7)继续往下分
（10）将G(0.7)分为N(0.6)和O(0.1)
（11）发现N(0.6)大于best(0.5)，则得到best(0.6)
（12）不像第（5）步，现在没有往上层返回的机会了。分枝定界结束
（13）最优位姿：best(0.6)，即N(0.6)

------下面的引用内容为以前的分析，是错的，不看---------

我们设置一个栈：stack，栈中，得分高的在顶上，得分低的在下面。

• 第一次循环
  先初始化一个best_score = 0.5
  B C 的贪心得分为：B(1.2), C(1.1)
  将B C放入stack中，将栈初始化。—— stack : (栈底) C(1.1) - B(1.2) (栈顶)
  将栈顶节点B取出 —— stack : (栈底) C (栈顶)
  判断：B(1.2) > best_score(0.5) 且 B不是叶子节点 —— 则继续进行分枝
  D E 的贪心得分为：D(1.0), E(0.8)
  将D E入栈，并按照得分排序 —— stack : (栈底) E(0.8) - D(1.0) - C(1.1) (栈顶)
• 第二次循环
  将栈顶节点C取出 —— stack : (栈底) E(0.8) - D(1.0) (栈顶)
  判断：C(1.1) > best_score(0.5) 且 C不是叶子节点 —— 则继续进行分枝
  F G 的贪心得分为：F(0.6), G(0.2)
  将F G入栈，并按照得分排序 —— stack : (栈底) G(0.2) - F(0.6) - E(0.8) - D(1.0)
  (栈顶)
• 第三次循环
  将栈顶节点D取出 —— stack : (栈底) G(0.2) - F(0.6) - E(0.8) (栈顶)
  判断：D(1.0) > best_score(0.5) 且 D不是叶子节点 —— 则继续进行分枝
  H I 的贪心得分为：H(0.7), I(0.2)
  将H I入栈，并按照得分排序 —— stack : (栈底) I(0.2) - G(0.2) - F(0.6) - H(0.7) -
  E(0.8) (栈顶)
• 第四次循环
  E出栈，J K入栈（具体略） —— **stack : (栈底) I(0.2) - G(0.2) - F(0.6) - J(0.65)

• H(0.7) - K(0.75) (栈顶)**

• 第五次循环
  K 出栈 —— stack : (栈底) I(0.2) - G(0.2) - F(0.6) - J(0.65) - H(0.7)
  (栈顶)
  判断： K(0.75) > best_score(0.5) 且 K 是叶子节点 —— 则更新best_score =
  0.75，最优解match = K的位姿
• 第六次循环
  H 出栈 —— *stack : (栈底) I(0.2) - G(0.2) - F(0.6) - J(0.65) (栈顶)
  判断： H(0.7) < best_score(0.75) —— 则不进行操作
• 第七次循环
  J 出栈 —— stack : (栈底) I(0.2) - G(0.2) - F(0.6) (栈顶)
  判断： J(0.65) < best_score(0.75) —— 则不进行操作
• 第八次循环
  F 出栈 —— stack : (栈底) I(0.2) - G(0.2) (栈顶)
  判断： F(0.6) < best_score(0.75)且F不为叶子节点 —— 则不进行操作

注意到了吧，上面这一步，把F出栈，然后不进行操作

这不就是剪枝嘛～！把中间节点及其子树

好了。。。。。。接下来不写了。。。。写到这里很累了。花了整整一晚上时间。

至于论文中的理论数学公式，累了。。。。。以后有时间再说。

有一些表达，看完我的blog，看完我那几篇参考的blog和知乎。。。。

也就都能理解了。。。。。

6.总结

分枝定界拆开

分枝：树搜索，扩展子节点的策略。

定界：每个节点的得分大于其所有子树叶子的得分，是其子树的“上界”

7.cartographer源代码补充

2020.5.17

我终于回来补充源代码的解读了！！！！！！！！！！！！！！！！！！！！！并更正一些之前的错误
从cartographer的起始阅读到现在得有半个月了吧。。。。
代码中有很多滴注释，冷藏口味更佳 😃

// cartographer的亮点所在！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！
// 分枝定界方法
// 初始传入的candidates为最上层的候选解
// 初始candidate_depth = 7
// 初始min_score为配置参数，为=0.55
Candidate2D FastCorrelativeScanMatcher2D::BranchAndBound(
    const std::vector<DiscreteScan2D>& discrete_scans,
    const SearchParameters& search_parameters,
    const std::vector<Candidate2D>& candidates, const int candidate_depth,
    float min_score) const {
  // 检查是否是最底层(叶子层)，如果已经查找到最底层了，则返回分数最高的候选解，排序在第一位的
  if (candidate_depth == 0) {
    // Return the best candidate.
    return *candidates.begin();
  }

  // Candidate2D的构造
  // 参数分别为：0：scan_index，即旋转序号。 0：x方向的偏移序号  0：y方向的偏移数   search_parameters：搜索参数
  Candidate2D best_high_resolution_candidate(0, 0, 0, search_parameters);
  
  best_high_resolution_candidate.score = min_score;
  
  // 对传入的候选人candidate进行循环，即从最上层开始遍历
  for (const Candidate2D& candidate : candidates) {
    // 将叶子节点与某棵分枝树的非叶子节点进行比较，如果非叶子节点的分数小于之前选出的最高分叶子节点，则直接将此非叶子节点candidate及其子树全部砍掉
    if (candidate.score <= min_score) {
      break;
    }
    
    // 一个容器，盛放这个节点candidate引出的四个下一层的候选者
    std::vector<Candidate2D> higher_resolution_candidates;
    
    // 区域边长右移，相当于步长减半，进行分枝
    const int half_width = 1 << (candidate_depth - 1);
    
    // 对x、y偏移进行遍历，求出这一个candidate的四个子节点候选人（即最上面遍历的那个元素）
    for (int x_offset : {0, half_width}) {  // 只能取0和half_width
      if (candidate.x_index_offset + x_offset >
          search_parameters.linear_bounds[candidate.scan_index].max_x) {  // 超出边界则break
        break;
      }
      for (int y_offset : {0, half_width}) {  // 只能取0和half_width   xy一共遍历四个子节点
        if (candidate.y_index_offset + y_offset >
            search_parameters.linear_bounds[candidate.scan_index].max_y) {  // 超出边界则break
          break;
        }
        // 候选者依次推进来，一共4个
        // 可以看出，分枝定界方法的分枝是向右下角的四个子节点进行分枝
        higher_resolution_candidates.emplace_back(
            candidate.scan_index, candidate.x_index_offset + x_offset,
            candidate.y_index_offset + y_offset, search_parameters);
      }
    }
    // 对candidate四个子节点进行打分，并将higher_resolution_candidates按照score从大到小的顺序进行排列
    ScoreCandidates(precomputation_grid_stack_->Get(candidate_depth - 1),
                    discrete_scans, search_parameters,
                    &higher_resolution_candidates);
    
    // 从此处开始递归，对分数最高的节点继续进行分支，直到最底层，然后再返回倒数第二层再进行迭代
    // 如果倒数第二层的最高分没有上一个的最底层（叶子层）的分数高，则跳过，否则继续向下进行评分
    
    // 从简单情况想，最上层节点就2个，树的深度就三层：2-1-0，每个父节点往下分两个子节点
    // 先对最上层的调用BranchAndBound1(父节点2个（1和2），candidate_depth == 2,min_score=0.55)->best_high_resolution_candidate初始化构造->令其得分为min_score0.55
    //		->对其中一个父节点（如1）分枝得到1.1和1.2，并进行打分，按顺序放入容器higher_resolution_candidates中 如<1.1, 1.2>代表1.1分更高->
    //		->使用std::max1（0.55,BB）但并未比较，跳入下一层BB函数的调用，保留对节点2的循环（当反向回来的时候会继续循环2）
    //                              |
    //                              ^
    //                              第二次调用BB2（父节点为<1.1, 1.2>，candidate_depth == 1, min_score=0.55）->best_high_resolution_candidate初始化构造->令其得分为min_score0.55
    //                              		->对选择其中一个父节点如1.1分枝得到1.1.1和1.1.2，并进行打分，按顺序放入容器higher_resolution_candidates中 如<1.1.2,1.1.1>代表1.1.2分最高
    //                              		->使用std::max2（0.55,BB）但并未比较，跳入下一层BB函数的调用，保留对节点1.2循环（当反向回来的时候会继续循环1.2）
    //  							    |
    //  							    ^
    //  							    第三次调用BB3（父节点为<1.1.2,1.1.1>，candidate_depth == 0, min_score=0.55）-> 触发if (candidate_depth == 0)返回最佳叶子节点1.1.2                          
    //                             ->跳回到上一层的BB2的std::max2（0.55,1.1.2的score）一般来说会比0.55大
    //                             ->更新best_high_resolution_candidate为1.1.2->
    //                             ->运行之前保留着的，对1.2的循环
    //                             ->可能会触发if (candidate.score <= min_score) 即 1.2的得分小于1.1.2的得分 直接break 那么1.2及其子树全部被减掉
    //                             ->如果没有被剪掉即上述条件不成立，那么将1.2分为两个子节点并排序<1.2.1，1.2.2>,使用std::max2（1.1.2的得分，BB）
    //                             												 |
    //                             												 ^
    //                             												 调用BB，触发if (candidate_depth == 0)返回这棵分枝树的最佳叶子节点1.2.1
    //                             ->跳回到上一层的BB2的std::max2（1.1.2的得分,1.2.1的得分）叶子节点之间进行较量 假如还是1.1.2大
    //                             // 即不管是减掉1.2及其子树还是将1.2分到叶子了，都是保持了best_high_resolution_candidate = 1.1.2
    //          ->跳回到BB1的std::max1（0.55,1.1.2的score）->保持best_high_resolution_candidate = 1.1.2
    //          ->运行之前的保留循环父节点2->有可能父节点2直接触发if (candidate.score <= min_score)即父节点2的得分小于1.1.2的得分
    //          ->父节点2极其子树全部被砍掉
    //          ->最终结束递归，输出最佳节点为：叶子节点1.1.2
    //                                                          
    
    
    best_high_resolution_candidate = std::max(
        best_high_resolution_candidate,
        BranchAndBound(discrete_scans, search_parameters,
                       higher_resolution_candidates, candidate_depth - 1,
                       best_high_resolution_candidate.score));
  }
  return best_high_resolution_candidate;
}

8.补充

8.1

实际上，cartographer会提前计算出不同分辨率下的表，一共七张表。每张表都对应了不同层的层栅格地图中栅格的log-odd得分（通过延伸区域进行得到，如第四节所说）。这样你把点云中的每一个激光点旋转过去落在某个map中的区域的时候，就直接查表得到这个区域的得分作为这个激光点的得分。
七张表存放在一个容器中：在fast_correlative_scan_matcher_2d.h的PrecomputationGridStack2D中：

 private:
   // 一个容器，容器中的每一个元素为树结构中的一层
   // 一共七层，深度为0-6，最上层索引为6，最下层索引为0
  std::vector<PrecomputationGrid2D> precomputation_grids_;

每一个表也都是fast_correlative_scan_matcher_2d.h的PrecomputationGrid2D类的成员变量：

  // Probabilites mapped to 0 to 255.
  std::vector<uint8> cells_;

这样扩展节点的时候，打分操作就可以直接实时查表了，而不是再进行旋转然后进行实时打分。能够大大提高实时性。

8.2

carto中的树结构一共七层，深度为0-6，最上层（最粗糙）索引为6，最下层（最精致）索引为0