【DDPM】一文看懂去噪扩散概率模型，公式讲解、代码实现与最全详解（二）

放风筝的猪

已于 2024-10-30 10:48:46 修改

阅读量1.3k

点赞数 10

分类专栏：扩散模型文章标签：人工智能计算机视觉超分辨率重建概率论

于 2024-10-23 21:59:35 首次发布

本文链接：https://blog.csdn.net/weixin_45897172/article/details/143194788

版权

扩散模型专栏收录该内容

5 篇文章

订阅专栏

四、代码实现（手写数字实例）

DDPM代码地址：This repo implements Denoising Diffusion Probabilistic Models (DDPM) in Pytorch
代码实现了使用DDPM训练和采样mnist 数字数据集

1. 扩散过程

现在让我们回顾一下扩散过程

前向过程：逐步为图像添加高斯噪声，生成噪声越来越大的图像版本，经过大量步骤后，它等效于从正态分布中采样的噪声，我们通过再每个时间步T上应用这个过度函数来实现
$\beta$ 是我们再T减1时添加到图像中的预定噪声，以获取时间步T的图像，将 $a_t$ 设为 $a_t = 1 - \beta$ ，并再时间步T计算这些的累计乘积，使我们能够再前向过程中从原始图像跳到任意时间步T的噪声图像
接着，我们让模型学习反向过程的分布，因为反向扩散过程与前向过程具有相同的函数形式，这里使高斯分布，我们本质上使希望模型学习预测它的均值和方差
再经过许多次推导后，从优化观察数据对数似然的初始目标出发，我们最终得出需要最小化以 $x_0$ 为条件的真实噪声分布与模型预测分布之间的KL散度
我们上面计算得出这个均值和方差，并由我们的模型预测分布
我们将方差固定为与目标分布完全相同，并以相同形式重写均值，之后，最小化KL散度实际上就是最小化预测噪声与原始噪声样本之间差异的平方

2. 训练方法伪代码

训练方法包括一个图像时间步T和一个噪声样本

并使用这个公式向模型输入再采样时间步T的噪声图像版本
累乘项需要来自噪声调度器，，它决定了随着时间步的推移所添加噪声的计划
损失函数成为原始噪声与模型预测值之间的均方误差

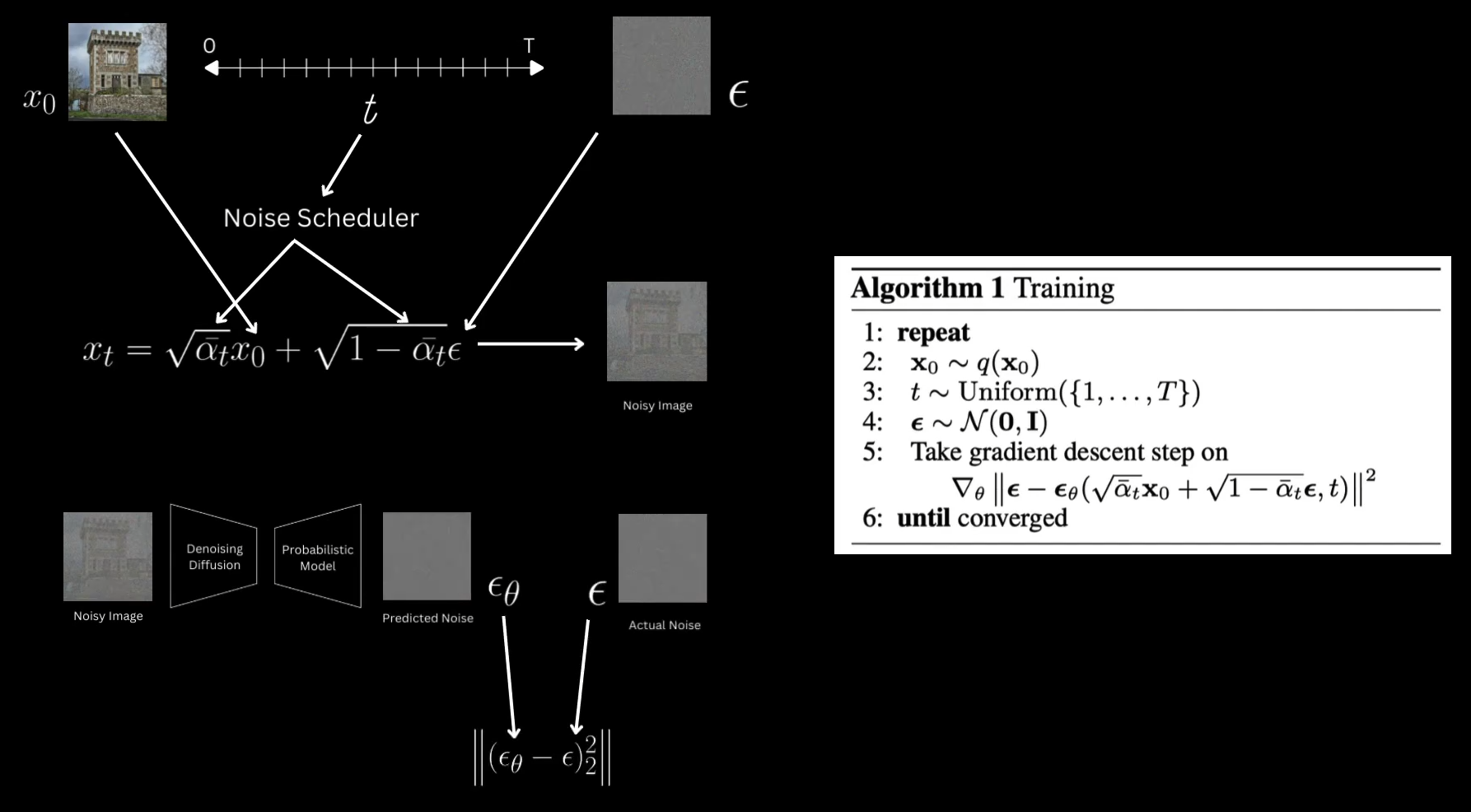
伪代码
1：repeat是一个循环（for … in range （#epochs））实际上论文中并不是用的epochs，而是iterations，epochs指的是遍历整个数据集一次，而iterations指的是一个batch
2：从数据集中取一个 $x_{0}$
3：取一个t ，这里从1到T之间取一个数，T=1000，uniform指的是均匀分布
4：取 $\mathcal{E}$
此时我们以及有了 $x_{0}$ ， $t$ ， $\mathcal{E}$ ，而且这些都是存在缓存中的，可以直接使用，通过公式
$x_t =\sqrt{1 - \overline{a}_t} × \mathcal{E} + \sqrt{\overline{a}_t}x_{0}$
5：小括号中是计算 $x_{0}$ ，此时我们就有了模型的输入
现在把 $x_{0}$ ， $t$ 送入UNet学习，UNet( $x_{0}$ ， $t$ )⇨ $\mathcal{E}'$

3. 采样方法伪代码

对于图像生成，我们只需从学习到的反向分布中采样，从正态分布的噪声样本 $x_{T}$ 开始，然后使用相同的公式计算均值，只是针对 $x_{T}$ 和噪声预测方差与条件为 $x_{t0}$ 的真实去噪分布相同，然后我们使用重参数化技巧从这个反向分布中采样，重复这一过程将我们带到 $x_{0}$ ，对于 $x_{0}$ ，我们步添加任何噪声，值返回均值
在这里插入图片描述

伪代码
1：生成过程中首先有一个服从正态分布的 $x_{T}$
2：一格一取 $t$ ，一步一步向前推，因为我们只有 $P(x_{t-1} | x_t)$ ，而没有 $P(x_{0} | x_t)$
3： $z$ 服从正态分布
4：这个公式就是我们上面推出来的正态分布式子（18），即做抽样得到一个全新的 $x_{t-1}$ ，最后得到 $x_{0}$ ，这个 $x_{0}$ 具有多样性

4. 创建一个噪声调度器

对于前向过程，给定一个图像，一个噪声样本和时间步t，它将使用前向公式返回该图像的噪声版本，为了高效的做到这点，它将存储 $a_t$ 和所有T的 $a_t$ 累乘乘积项，作者使用线性噪声调度器，在1000各时间步内将 $\beta$ 从1e-4线性增加到0.02
这个调度器的第二个职责是，给定 $x_T$ 和模型的噪声预测，它将通过从反向分布中采样为我们提供 $x_T$ 减1，为此，它将根据各自的公式计算均值和方差，并使用重参数化技巧从这个分布中返回一个样本
为此，我们还存储 $1 - a_t$ ， $\overline{a}_t$ ， $\sqrt{1 - \overline{a}_t}$ 。我们可以在运行时计算所有这些，但预先计算它们可以大大简化公式的代码。

创建文件linear_noise_scheduler.py

import torch


class LinearNoiseScheduler:
    r"""
    Class for the linear noise scheduler that is used in DDPM (Denoising Diffusion Probabilistic Model).
    用于 DDPM 的线性噪声调度器类。
    """
    def __init__(self, num_timesteps, beta_start, beta_end):
        """
        初始化线性噪声调度器
        
        :param num_timesteps: 时间步长的数量
        :param beta_start: 噪声因子的起始值
        :param beta_end: 噪声因子的结束值
        """
        self.num_timesteps = num_timesteps  # 时间步长数量
        self.beta_start = beta_start        # beta 起始值
        self.beta_end = beta_end            # beta 结束值
        
        # 在 [beta_start, beta_end] 区间内生成等间隔的 beta 值
        self.betas = torch.linspace(beta_start, beta_end, num_timesteps)
        
        # 计算 alpha 值，alpha = 1 - beta
        self.alphas = 1. - self.betas
        
        # 累乘所有时间步的 alpha 值，即 alpha 累积积
        self.alpha_cum_prod = torch.cumprod(self.alphas, dim=0)
        
        # 计算 sqrt(alpha 累积积) 和 sqrt(1 - alpha 累积积)，
        # 分别用于之后的加噪和反向采样过程
        self.sqrt_alpha_cum_prod = torch.sqrt(self.alpha_cum_prod)
        self.sqrt_one_minus_alpha_cum_prod = torch.sqrt(1 - self.alpha_cum_prod)
        
    def add_noise(self, original, noise, t):
        r"""
        给原始图片加噪声的前向扩散过程
        
        :param original: 原始图像
        :param noise: 随机噪声张量（从正态分布中生成）
        :param t: 当前时间步的索引，形状为 (B,)
        :return: 加噪后的图像
        """
        original_shape = original.shape  # 获取原始图像的形状
        batch_size = original_shape[0]   # 批次大小
        
        # 取出当前时间步对应的 sqrt(alpha 累积积) 和 sqrt(1 - alpha 累积积)
        sqrt_alpha_cum_prod = self.sqrt_alpha_cum_prod.to(original.device)[t].reshape(batch_size)
        sqrt_one_minus_alpha_cum_prod = self.sqrt_one_minus_alpha_cum_prod.to(original.device)[t].reshape(batch_size)
        
        # 将 (B,) 的形状扩展为 (B,1,1,1)，以匹配图像的形状 (B,C,H,W)
        for _ in range(len(original_shape) - 1):
            sqrt_alpha_cum_prod = sqrt_alpha_cum_prod.unsqueeze(-1)
        for _ in range(len(original_shape) - 1):
            sqrt_one_minus_alpha_cum_prod = sqrt_one_minus_alpha_cum_prod.unsqueeze(-1)
        
        # 使用前向扩散公式对图像加噪：
        # 加噪后的图像 = sqrt(alpha 累积积) * 原图 + sqrt(1 - alpha 累积积) * 噪声
        return (sqrt_alpha_cum_prod.to(original.device) * original
                + sqrt_one_minus_alpha_cum_prod.to(original.device) * noise)
        
    def sample_prev_timestep(self, xt, noise_pred, t):
        r"""
        从当前时间步 xt 和模型预测的噪声 noise_pred 采样出前一时间步的样本 xt-1
        
        :param xt: 当前时间步的样本
        :param noise_pred: 模型预测的噪声
        :param t: 当前时间步的索引
        :return: 采样出的前一时间步 xt-1 和去噪后估计的 x0
        """
        # 反向计算 x0（去噪后的原始图像估计）
        x0 = ((xt - (self.sqrt_one_minus_alpha_cum_prod.to(xt.device)[t] * noise_pred)) /
              torch.sqrt(self.alpha_cum_prod.to(xt.device)[t]))
        
        # 将 x0 的值限制在 [-1, 1] 之间
        x0 = torch.clamp(x0, -1., 1.)
        
        # 计算前一时间步的均值 (mean)
        mean = xt - ((self.betas.to(xt.device)[t]) * noise_pred) / (self.sqrt_one_minus_alpha_cum_prod.to(xt.device)[t])
        mean = mean / torch.sqrt(self.alphas.to(xt.device)[t])
        
        if t == 0:
            # 如果当前是第一个时间步，直接返回均值
            return mean, x0
        else:
            # 否则，计算方差 (variance) 和标准差 (sigma)，并进行随机扰动
            variance = (1 - self.alpha_cum_prod.to(xt.device)[t - 1]) / (1.0 - self.alpha_cum_prod.to(xt.device)[t])
            variance = variance * self.betas.to(xt.device)[t]
            sigma = variance ** 0.5
            z = torch.randn(xt.shape).to(xt.device)  # 从标准正态分布中采样随机噪声 z
            
            # 返回加了扰动的均值和去噪后的 x0
            return mean + sigma * z, x0

这就完成了整个噪声调度器，它处理添加噪声的前向过程和采样的反向过程

5. 模型

对于扩散模型，我们实际上可以使用任何架构，只要满足两个要求
在这里插入图片描述

第一个要求是输入和输出的形状必须相同
另一个要求是某种机制来融合时间步信息（原因：无论在训练还是采样中，我们总是可以获得当前时间步的信息，，事实上，知道我们处于哪个时间步将有助于模型预测原始噪声，因为我们提供了关于输入图像有多少实际上是噪声的信息。因此我们不仅仅是给模型一个图像，还给它我们所在的时间步）
-这里使用UNet，也是作者使用的

5.1 时间嵌入块

在这里插入图片描述

它将接收一个大小为B的1D张量的时间步，B即为批次大小，并为批次中的每个时间步提供一个思维张量表示，时间嵌入快将首先使用嵌入空间将整数时间步转换为某种向量表示
然后，它将被送入两个线性层，中间由激活分割，以提供我们的最终时间步表示，对于嵌入空间，作者使用了在Transformer中使用的正弦位置嵌入，对于所有地方的激活，我使用了Sigmoid线性单元，但你也可以选择不同的激活函数

5.2 UNet

在这里插入图片描述
它本质上是一种编码器，解码器结构，其中编码器是一系列下采样块，每个块都会减少输入的大小，通常减少一半。并增加通道数量，最后一个下采样块的输出传递到中间快的各层，这些层都在相同的空间分辨率下工作，之后，有一系列上采样块，这些块一个一个增加空间大小，并减少通道数量，最终匹配模型的输入大小，上采样块还通过残差跳跃连接，融合来自相同分辨率下的对应下采样块的输出

5.2.1 下采样块

在这里插入图片描述

几乎所有变化的下采样块都会是一个ResNet块，接着是一个自注意力块，然后是一个下采样块
对于ResNet加自注意力块，我们将一组归一化，然后是激活，再是卷积层，该输出将再次传递给一个归一化，激活和卷积层，我们将从第一个归一化层的输入到第二个卷积层的输出添加一个残差连接，整个过程称为ResNet块，你可以将其视为两个卷积快加一个残差连接，然后是一个归一化和一个自注意力层，还有一个残差连接，我们有多个这样的ResNet加自注意力层
我们还需要融合时间信息，其方式是每个ResNet块都有一个激活，然后是一个线性层，我们首先将其通过时间嵌入表示，再将其添加到第一个卷积层的输出中
因此，本质上，这个线性层将时间步表示投影到与卷积层输出中的通道大小相同的张量中，这样，通过跨越空间维度复制这个时间步表示，这两者可以相加
为了简化，我们将将这个部分的所有内容替换为ResNet块和自注意力块

5.2.2 上采样块

在这里插入图片描述

上采样块和下采样块完全相同，只是它首先将输入上采样到两倍空间大小，然后再通道维度上连接相同空间分辨率的下采样块输出，所以，它是相同的ResNet和自注意力快层

5.2.3 中间块

中间块的各层始终保持输入的相同空间分辨率，首先是一个ResNet块，然后是自注意力和ResNet层
对于这些ResNet块中的每一个，我们都有一个时间步投影层，就是激活后跟一个线性层，现在的时间步表示通过这些块后，才添加到ResNet块的第一个卷积层的输出中

6. UNet代码

我们要做的第一件事是实现正弦位置嵌入代码

def get_time_embedding(time_steps, temb_dim):
    r"""
    将时间步长张量转换为嵌入表示，使用正弦余弦时间嵌入公式
    :param time_steps: 形状为 (B,) 的一维张量，表示批量中的时间步长
    :param temb_dim: 嵌入维度，表示生成的时间嵌入的维度大小
    :return: 形状为 (B, D) 的嵌入表示，B 是批量大小，D 是嵌入维度
    这个方法所做的是使用固定的嵌入空间将整数时间步表示嵌入
    """
    # 确保嵌入维度是偶数，因为嵌入要分为 sin 和 cos 两部分
    assert temb_dim % 2 == 0, "time embedding dimension must be divisible by 2"
    
    # 计算用于正弦余弦函数的频率因子 factor = 10000^(2i/temb_dim)
    # 即位置（这里是时间步整数值）将再正弦和余弦函数中被除以一切，这将为我们提供从0到时间嵌入维度大小的一半的所有值，之所以是一半，是因为我们将正弦和余弦连接起来
    # 其中 i 表示维度索引，temb_dim // 2 代表频率的维度大小，公式来源于 Transformer 中的位置编码
    factor = 10000 ** ((torch.arange(
        start=0, end=temb_dim // 2, dtype=torch.float32, device=time_steps.device) / (temb_dim // 2))
    )
    
    # 将时间步张量 time_steps 扩展以适应嵌入维度
    # time_steps 形状 (B,) -> (B, 1) -> (B, temb_dim // 2) ，每个时间步都除以频率因子 factor
    t_emb = time_steps[:, None].repeat(1, temb_dim // 2) / factor
    
    # 将计算得到的值通过正弦和余弦函数生成嵌入
    # t_emb 形状 (B, temb_dim // 2)，通过 torch.cat() 函数沿着最后一维将 sin 和 cos 拼接，形成 (B, temb_dim)
    t_emb = torch.cat([torch.sin(t_emb), torch.cos(t_emb)], dim=-1)
    
    # 返回最终的时间嵌入，形状为 (B, temb_dim)
    return t_emb

实现下采样，下面是我们需要实现的块：
ResNet将由两个归一化，激活，卷积层加上残差组成，归一化和自注意力，我们还需要时间投影层，它将时间嵌入投影到与第一个卷积特征图输出通道数相同的维度

class DownBlock(nn.Module):
    r"""
    含有注意力机制的下采样卷积块。
    该块包含以下步骤：
    1. 带有时间嵌入的 ResNet 块
    2. 注意力机制块
    3. 使用 2x2 平均池化进行下采样
    """
    def __init__(self, in_channels, out_channels, t_emb_dim,
                 down_sample=True, num_heads=4, num_layers=1):
        super().__init__()
        
        # 定义层数和是否进行下采样
        self.num_layers = num_layers
        self.down_sample = down_sample
        
        # 第一个 ResNet 卷积块 (包含 num_layers 层)
        self.resnet_conv_first = nn.ModuleList(
            [
                nn.Sequential(
                    # 使用 GroupNorm 归一化层，激活函数 SiLU（Swish），然后 3x3 卷积
                    nn.GroupNorm(8, in_channels if i == 0 else out_channels),
                    nn.SiLU(),
                    nn.Conv2d(in_channels if i == 0 else out_channels, out_channels,
                              kernel_size=3, stride=1, padding=1),
                )
                for i in range(num_layers)
            ]
        )
        
        # 时间嵌入层，用于与特征图结合
        self.t_emb_layers = nn.ModuleList([
            nn.Sequential(
                nn.SiLU(),  # SiLU 激活函数
                nn.Linear(t_emb_dim, out_channels)  # 线性层，将时间嵌入映射到输出通道
            )
            for _ in range(num_layers)
        ])
        
        # 第二个 ResNet 卷积块 (包含 num_layers 层)
        self.resnet_conv_second = nn.ModuleList(
            [
                nn.Sequential(
                    nn.GroupNorm(8, out_channels),
                    nn.SiLU(),
                    nn.Conv2d(out_channels, out_channels,
                              kernel_size=3, stride=1, padding=1),
                )
                for _ in range(num_layers)
            ]
        )
        
        # 注意力机制的归一化层（GroupNorm），用于多头注意力层之前
        self.attention_norms = nn.ModuleList(
            [nn.GroupNorm(8, out_channels)
             for _ in range(num_layers)]
        )
        
        # 多头注意力层，输入通道为 out_channels，注意力头数为 num_heads
        self.attentions = nn.ModuleList(
            [nn.MultiheadAttention(out_channels, num_heads, batch_first=True)
             for _ in range(num_layers)]
        )
        
        # 残差连接的 1x1 卷积层，用于调整输入通道数到输出通道数
        self.residual_input_conv = nn.ModuleList(
            [
                nn.Conv2d(in_channels if i == 0 else out_channels, out_channels, kernel_size=1)
                for i in range(num_layers)
            ]
        )
        
        # 下采样卷积层，如果 down_sample 为 True，则使用 4x4 卷积进行 2 倍下采样
        self.down_sample_conv = nn.Conv2d(out_channels, out_channels,
                                          4, 2, 1) if self.down_sample else nn.Identity()
    
    def forward(self, x, t_emb):
        # 输入张量 x 和时间嵌入 t_emb，进行前向传播
        out = x
        
        # 遍历每一层的 ResNet 块和注意力块
        for i in range(self.num_layers):
            
            # ResNet 块的第一个卷积
            resnet_input = out
            out = self.resnet_conv_first[i](out)
            
            # 加入时间嵌入，通过广播 (B, D) -> (B, D, 1, 1) 将 t_emb 与特征图结合
            out = out + self.t_emb_layers[i](t_emb)[:, :, None, None]
            
            # ResNet 块的第二个卷积
            out = self.resnet_conv_second[i](out)
            
            # 残差连接：输入的 resnet_input 通过 1x1 卷积后加回输出
            out = out + self.residual_input_conv[i](resnet_input)
            
            # 注意力机制块
            # 先将 out 的形状从 (B, C, H, W) 转换为 (B, C, H*W)，准备输入注意力层
            batch_size, channels, h, w = out.shape
            in_attn = out.reshape(batch_size, channels, h * w)
            
            # 在进入多头注意力之前对其进行归一化，并转置以匹配 MultiheadAttention 输入格式
            in_attn = self.attention_norms[i](in_attn)
            in_attn = in_attn.transpose(1, 2)
            
            # 计算多头注意力，返回的 out_attn 再转置回原来的形状
            out_attn, _ = self.attentions[i](in_attn, in_attn, in_attn)
            out_attn = out_attn.transpose(1, 2).reshape(batch_size, channels, h, w)
            
            # 将注意力输出加回原始特征图，形成残差
            out = out + out_attn
            
        # 如果 down_sample 为 True，进行下采样（2x2 平均池化）
        out = self.down_sample_conv(out)
        
        # 返回输出特征图
        return out

中间块

class MidBlock(nn.Module):
    r"""
    含有注意力机制的中间卷积块。
    该块包含以下步骤：
    1. 带有时间嵌入的 ResNet 块
    2. 注意力机制块
    3. 带有时间嵌入的 ResNet 块
    """
    def __init__(self, in_channels, out_channels, t_emb_dim, num_heads=4, num_layers=1):
        super().__init__()
        
        # 定义层数
        self.num_layers = num_layers
        
        # 第一个 ResNet 块：多层卷积和激活函数，用于将输入特征进行变换
        self.resnet_conv_first = nn.ModuleList(
            [
                nn.Sequential(
                    nn.GroupNorm(8, in_channels if i == 0 else out_channels),  # GroupNorm 归一化层
                    nn.SiLU(),  # SiLU 激活函数
                    nn.Conv2d(in_channels if i == 0 else out_channels, out_channels,
                              kernel_size=3, stride=1, padding=1),  # 3x3 卷积
                )
                for i in range(num_layers+1)
            ]
        )
        
        # 时间嵌入层，用于与特征图结合，结合 ResNet 的输出
        self.t_emb_layers = nn.ModuleList([
            nn.Sequential(
                nn.SiLU(),  # SiLU 激活函数
                nn.Linear(t_emb_dim, out_channels)  # 线性层，将时间嵌入映射到输出通道
            )
            for _ in range(num_layers + 1)
        ])
        
        # 第二个 ResNet 卷积块 (与第一个对应)，用于进一步处理输入特征
        self.resnet_conv_second = nn.ModuleList(
            [
                nn.Sequential(
                    nn.GroupNorm(8, out_channels),
                    nn.SiLU(),
                    nn.Conv2d(out_channels, out_channels,
                              kernel_size=3, stride=1, padding=1),  # 3x3 卷积
                )
                for _ in range(num_layers+1)
            ]
        )
        
        # 注意力机制的归一化层（GroupNorm），用于多头注意力层之前
        self.attention_norms = nn.ModuleList(
            [nn.GroupNorm(8, out_channels)
                for _ in range(num_layers)]
        )
        
        # 多头注意力层，输入通道为 out_channels，注意力头数为 num_heads
        self.attentions = nn.ModuleList(
            [nn.MultiheadAttention(out_channels, num_heads, batch_first=True)
                for _ in range(num_layers)]
        )
        
        # 残差连接的 1x1 卷积层，用于调整输入通道数到输出通道数
        self.residual_input_conv = nn.ModuleList(
            [
                nn.Conv2d(in_channels if i == 0 else out_channels, out_channels, kernel_size=1)
                for i in range(num_layers+1)
            ]
        )
    
    def forward(self, x, t_emb):
        # 输入张量 x 和时间嵌入 t_emb，进行前向传播
        out = x
        
        # 第一个 ResNet 块
        resnet_input = out
        out = self.resnet_conv_first[0](out)  # 卷积
        out = out + self.t_emb_layers[0](t_emb)[:, :, None, None]  # 加入时间嵌入
        out = self.resnet_conv_second[0](out)  # 第二个卷积
        out = out + self.residual_input_conv[0](resnet_input)  # 残差连接
        
        # 循环处理 num_layers 次注意力块和 ResNet 块
        for i in range(self.num_layers):
            
            # 注意力机制块
            batch_size, channels, h, w = out.shape  # 获取输入的形状
            in_attn = out.reshape(batch_size, channels, h * w)  # 调整形状用于注意力计算
            in_attn = self.attention_norms[i](in_attn)  # 归一化
            in_attn = in_attn.transpose(1, 2)  # 转置为 (B, H*W, C)
            
            # 计算多头注意力，输出注意力后的特征
            out_attn, _ = self.attentions[i](in_attn, in_attn, in_attn)
            out_attn = out_attn.transpose(1, 2).reshape(batch_size, channels, h, w)  # 恢复形状
            out = out + out_attn  # 残差连接
            
            # ResNet 块
            resnet_input = out
            out = self.resnet_conv_first[i+1](out)  # 卷积
            out = out + self.t_emb_layers[i+1](t_emb)[:, :, None, None]  # 加入时间嵌入
            out = self.resnet_conv_second[i+1](out)  # 第二个卷积
            out = out + self.residual_input_conv[i+1](resnet_input)  # 残差连接
        
        # 返回输出特征图
        return out

上采样块

class UpBlock(nn.Module):
    r"""
    含有注意力机制的上采样卷积块。
    该块的主要流程包括以下步骤：
    1. 上采样
    2. 将下采样块的输出拼接 (Concatenate) 到上采样结果
    3. 带有时间嵌入的 ResNet 块
    4. 注意力机制块
    """
    def __init__(self, in_channels, out_channels, t_emb_dim, up_sample=True, num_heads=4, num_layers=1):
        super().__init__()
        
        # 层数和是否进行上采样
        self.num_layers = num_layers
        self.up_sample = up_sample
        
        # ResNet 块的第一个卷积部分，包含归一化层、激活函数、卷积层
        self.resnet_conv_first = nn.ModuleList(
            [
                nn.Sequential(
                    nn.GroupNorm(8, in_channels if i == 0 else out_channels),  # GroupNorm 归一化层
                    nn.SiLU(),  # SiLU 激活函数
                    nn.Conv2d(in_channels if i == 0 else out_channels, out_channels, kernel_size=3, stride=1, padding=1),  # 3x3 卷积
                )
                for i in range(num_layers)  # 根据层数创建多个块
            ]
        )
        
        # 时间嵌入层，结合时间信息，用于与 ResNet 卷积块结合
        self.t_emb_layers = nn.ModuleList([
            nn.Sequential(
                nn.SiLU(),  # SiLU 激活函数
                nn.Linear(t_emb_dim, out_channels)  # 线性层将时间嵌入映射到输出通道
            )
            for _ in range(num_layers)
        ])
        
        # ResNet 块的第二个卷积部分，类似于第一个卷积部分
        self.resnet_conv_second = nn.ModuleList(
            [
                nn.Sequential(
                    nn.GroupNorm(8, out_channels),  # GroupNorm 归一化层
                    nn.SiLU(),  # SiLU 激活函数
                    nn.Conv2d(out_channels, out_channels, kernel_size=3, stride=1, padding=1),  # 3x3 卷积
                )
                for _ in range(num_layers)
            ]
        )
        
        # 注意力机制的归一化层
        self.attention_norms = nn.ModuleList(
            [
                nn.GroupNorm(8, out_channels)
                for _ in range(num_layers)
            ]
        )
        
        # 多头注意力机制，用于处理特征图的长距离依赖关系
        self.attentions = nn.ModuleList(
            [
                nn.MultiheadAttention(out_channels, num_heads, batch_first=True)
                for _ in range(num_layers)
            ]
        )
        
        # 残差连接所使用的卷积层，用于调整输入通道数到输出通道数
        self.residual_input_conv = nn.ModuleList(
            [
                nn.Conv2d(in_channels if i == 0 else out_channels, out_channels, kernel_size=1)
                for i in range(num_layers)
            ]
        )
        
        # 上采样卷积层，用于将输入的分辨率扩大一倍，使用 ConvTranspose2d 实现反卷积
        self.up_sample_conv = nn.ConvTranspose2d(in_channels // 2, in_channels // 2,
                                                 kernel_size=4, stride=2, padding=1) \
            if self.up_sample else nn.Identity()  # 如果不需要上采样，则使用 Identity 操作
    
    def forward(self, x, out_down, t_emb):
        """
        前向传播过程：
        x: 输入特征图
        out_down: 下采样块的输出，用于拼接
        t_emb: 时间嵌入
        """
        # 上采样输入特征图 x
        x = self.up_sample_conv(x)
        
        # 将上采样后的结果与下采样块输出 out_down 拼接
        x = torch.cat([x, out_down], dim=1)
        
        out = x
        for i in range(self.num_layers):
            # ResNet 第一层卷积
            resnet_input = out
            out = self.resnet_conv_first[i](out)
            
            # 加入时间嵌入信息
            out = out + self.t_emb_layers[i](t_emb)[:, :, None, None]
            
            # ResNet 第二层卷积
            out = self.resnet_conv_second[i](out)
            
            # 残差连接
            out = out + self.residual_input_conv[i](resnet_input)
            
            # 获取特征图形状，准备进行注意力机制
            batch_size, channels, h, w = out.shape
            in_attn = out.reshape(batch_size, channels, h * w)  # 调整形状用于注意力计算
            in_attn = self.attention_norms[i](in_attn)  # 注意力前的归一化
            in_attn = in_attn.transpose(1, 2)  # 转置为 (batch_size, H*W, channels)
            
            # 多头注意力计算
            out_attn, _ = self.attentions[i](in_attn, in_attn, in_attn)
            
            # 恢复形状并加入到输出中
            out_attn = out_attn.transpose(1, 2).reshape(batch_size, channels, h, w)
            out = out + out_attn  # 残差连接注意力结果

        # 返回处理后的输出特征图
        return out

unet类

class Unet(nn.Module):
    r"""
    Unet 模型由下采样块 (Down blocks)、中间块 (Midblocks) 和上采样块 (Up blocks) 组成。
    """
    def __init__(self, model_config):
        super().__init__()
        
        # 从模型配置中提取参数
        im_channels = model_config['im_channels']  # 输入图像的通道数
        self.down_channels = model_config['down_channels']  # 下采样各层的通道数
        self.mid_channels = model_config['mid_channels']  # 中间块的通道数
        self.t_emb_dim = model_config['time_emb_dim']  # 时间嵌入维度
        self.down_sample = model_config['down_sample']  # 是否在每一层执行下采样
        self.num_down_layers = model_config['num_down_layers']  # 每个下采样块中的层数
        self.num_mid_layers = model_config['num_mid_layers']  # 每个中间块中的层数
        self.num_up_layers = model_config['num_up_layers']  # 每个上采样块中的层数
        
        # 断言检查通道数的一致性
        assert self.mid_channels[0] == self.down_channels[-1]  # 中间块的第一层通道数与下采样最后一层一致
        assert self.mid_channels[-1] == self.down_channels[-2]  # 中间块的最后一层通道数与下采样倒数第二层一致
        assert len(self.down_sample) == len(self.down_channels) - 1  # 下采样的配置应与通道数列表长度对应

        # 时间嵌入的初始投影层
        self.t_proj = nn.Sequential(
            nn.Linear(self.t_emb_dim, self.t_emb_dim),  # 线性层，用于处理时间嵌入
            nn.SiLU(),  # SiLU 激活函数
            nn.Linear(self.t_emb_dim, self.t_emb_dim)  # 另一个线性层
        )

        # 翻转下采样的顺序，供上采样使用
        self.up_sample = list(reversed(self.down_sample))
        
        # 输入图像的初始卷积，映射到第一个下采样块的通道数
        self.conv_in = nn.Conv2d(im_channels, self.down_channels[0], kernel_size=3, padding=(1, 1))
        
        # 下采样块的定义
        self.downs = nn.ModuleList([])
        for i in range(len(self.down_channels) - 1):
            self.downs.append(DownBlock(self.down_channels[i], self.down_channels[i + 1], self.t_emb_dim,
                                        down_sample=self.down_sample[i], num_layers=self.num_down_layers))
        
        # 中间块的定义
        self.mids = nn.ModuleList([])
        for i in range(len(self.mid_channels) - 1):
            self.mids.append(MidBlock(self.mid_channels[i], self.mid_channels[i + 1], self.t_emb_dim,
                                      num_layers=self.num_mid_layers))
        
        # 上采样块的定义，倒序创建
        self.ups = nn.ModuleList([])
        for i in reversed(range(len(self.down_channels) - 1)):
            # 如果是最后一个上采样块，输出的通道数为 16
            self.ups.append(UpBlock(self.down_channels[i] * 2, self.down_channels[i - 1] if i != 0 else 16,
                                    self.t_emb_dim, up_sample=self.down_sample[i], num_layers=self.num_up_layers))
        
        # 输出的归一化层
        self.norm_out = nn.GroupNorm(8, 16)
        
        # 输出的卷积层，映射回原始的图像通道数
        self.conv_out = nn.Conv2d(16, im_channels, kernel_size=3, padding=1)
    
    def forward(self, x, t):
        """
        前向传播过程：
        x: 输入图像
        t: 时间嵌入，用于处理时间信息
        """
        # 对输入图像进行第一次卷积
        out = self.conv_in(x)
        # 输出形状为 B x C1 x H x W
        
        # 获取时间嵌入，将 t 转为张量，并通过时间嵌入投影层
        t_emb = get_time_embedding(torch.as_tensor(t).long(), self.t_emb_dim)
        t_emb = self.t_proj(t_emb)
        
        down_outs = []  # 存储每个下采样块的输出，用于后续上采样阶段
        
        # 逐个通过下采样块
        for idx, down in enumerate(self.downs):
            down_outs.append(out)  # 将每个下采样块的输出保存
            out = down(out, t_emb)  # 将输出传递到下一个块
        # 下采样块输出 [B x C1 x H x W, B x C2 x H/2 x W/2, B x C3 x H/4 x W/4]
        # 最终输出 out: B x C4 x H/4 x W/4
            
        # 通过中间块处理
        for mid in self.mids:
            out = mid(out, t_emb)
        # 中间块输出 out: B x C3 x H/4 x W/4
        
        # 逐个通过上采样块
        for up in self.ups:
            down_out = down_outs.pop()  # 取出对应的下采样输出，用于拼接
            out = up(out, down_out, t_emb)  # 传入上采样块
            # 上采样块输出 [B x C2 x H/4 x W/4, B x C1 x H/2 x W/2, B x 16 x H x W]
        
        # 最终输出通过归一化层和激活函数
        out = self.norm_out(out)
        out = nn.SiLU()(out)
        
        # 最终输出通过卷积层，映射到输入图像的通道数
        out = self.conv_out(out)
        # 输出形状 B x C x H x W
        
        return out

7. mnist_dataset.py

import glob
import os

import torchvision
from PIL import Image
from tqdm import tqdm  # 用于显示进度条
from torch.utils.data.dataloader import DataLoader  # PyTorch 的数据加载器
from torch.utils.data.dataset import Dataset  # PyTorch 的数据集基类


class MnistDataset(Dataset):
    r"""
    一个简单的用于 MNIST 图片数据集的自定义 Dataset 类。
    通过自定义 Dataset 而不是使用 torchvision 中的 Dataset，是为了能够替换成其他图片数据集。
    """
    def __init__(self, split, im_path, im_ext='png'):
        r"""
        初始化方法，用于设置数据集属性。
        :param split: 表示数据集的划分（train/test），用于定位图片文件夹
        :param im_path: 图片数据集的根目录路径
        :param im_ext: 图片的文件扩展名，默认为 'png'，假设所有图片的扩展名相同
        """
        self.split = split  # 保存数据集划分信息，例如训练集或测试集
        self.im_ext = im_ext  # 图片文件的扩展名
        self.images, self.labels = self.load_images(im_path)  # 加载图片路径和对应的标签
    
    def load_images(self, im_path):
        r"""
        加载指定路径中的所有图片，并将它们和对应的标签存储起来。
        :param im_path: 图片根路径
        :return: 返回图片路径列表和对应的标签列表
        """
        # 检查图片路径是否存在
        assert os.path.exists(im_path), "images path {} does not exist".format(im_path)
        
        ims = []  # 用于存储图片路径
        labels = []  # 用于存储对应的标签
        # 遍历图片目录中的每个子文件夹（文件夹名为图片的类别标签）
        for d_name in tqdm(os.listdir(im_path)):  # tqdm 用于显示进度条
            # 搜索文件夹下所有符合扩展名的图片
            for fname in glob.glob(os.path.join(im_path, d_name, '*.{}'.format(self.im_ext))):
                ims.append(fname)  # 将图片的路径加入列表
                labels.append(int(d_name))  # 文件夹名被当作图片的类别标签，加入标签列表
        # 打印找到的图片数量和数据集划分信息
        print('Found {} images for split {}'.format(len(ims), self.split))
        return ims, labels  # 返回图片路径列表和标签列表
    
    def __len__(self):
        r"""
        返回数据集的大小，即图片数量。
        :return: 图片的数量
        """
        return len(self.images)
    
    def __getitem__(self, index):
        r"""
        根据索引获取图片和其对应的标签，并将图片转换为张量。
        :param index: 数据集中的索引
        :return: 转换为张量的图片
        """
        im = Image.open(self.images[index])  # 打开图片文件
        im_tensor = torchvision.transforms.ToTensor()(im)  # 将图片转换为 PyTorch 张量
        
        # 将像素值范围从 [0, 1] 转换为 [-1, 1]，这样模型就可以持续看到与随机噪声相比具有相似比例的图像
        im_tensor = (2 * im_tensor) - 1
        return im_tensor  # 返回处理后的图片张量

8. train_ddpm.py

import torch
import yaml
import argparse
import os
import numpy as np
from tqdm import tqdm  # 用于显示进度条
from torch.optim import Adam  # Adam 优化器
from dataset.mnist_dataset import MnistDataset  # 自定义的 MNIST 数据集类
from torch.utils.data import DataLoader  # 数据加载器
from models.unet_base import Unet  # 自定义的 UNet 模型
from scheduler.linear_noise_scheduler import LinearNoiseScheduler  # 线性噪声调度器

# 设置设备为 GPU 或 CPU，根据是否有可用的 CUDA 设备
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')


def train(args):
    """
    训练函数，执行训练步骤。
    :param args: 从命令行传递的参数，包括配置文件路径
    """
    # 读取配置文件
    with open(args.config_path, 'r') as file:
        try:
            config = yaml.safe_load(file)  # 使用 yaml 加载配置文件
        except yaml.YAMLError as exc:
            print(exc)
    print(config)  # 输出加载的配置信息
    
    # 从配置文件中提取不同模块的参数
    diffusion_config = config['diffusion_params']  # 噪声调度器相关参数
    dataset_config = config['dataset_params']  # 数据集相关参数
    model_config = config['model_params']  # 模型结构参数
    train_config = config['train_params']  # 训练相关参数
    
    # 创建噪声调度器，线性调度噪声的 beta 参数
    scheduler = LinearNoiseScheduler(num_timesteps=diffusion_config['num_timesteps'],
                                     beta_start=diffusion_config['beta_start'],
                                     beta_end=diffusion_config['beta_end'])
    
    # 加载 MNIST 数据集
    mnist = MnistDataset('train', im_path=dataset_config['im_path'])
    mnist_loader = DataLoader(mnist, batch_size=train_config['batch_size'], shuffle=True, num_workers=4)
    
    # 实例化 UNet 模型
    model = Unet(model_config).to(device)
    model.train()  # 将模型设置为训练模式
    
    # 创建输出目录，用于保存模型检查点和日志
    if not os.path.exists(train_config['task_name']):
        os.mkdir(train_config['task_name'])
    
    # 如果找到现有检查点文件，则加载模型权重
    if os.path.exists(os.path.join(train_config['task_name'],train_config['ckpt_name'])):
        print('Loading checkpoint as found one')
        model.load_state_dict(torch.load(os.path.join(train_config['task_name'],
                                                      train_config['ckpt_name']), map_location=device))
    
    # 设置训练的相关参数
    num_epochs = train_config['num_epochs']  # 训练轮数
    optimizer = Adam(model.parameters(), lr=train_config['lr'])  # Adam 优化器
    criterion = torch.nn.MSELoss()  # 损失函数为均方误差 (MSE)
    
    # 训练循环
    for epoch_idx in range(num_epochs):
        losses = []  # 保存每个 batch 的损失值
        for im in tqdm(mnist_loader):  # 使用 tqdm 显示训练进度
            optimizer.zero_grad()  # 梯度归零
            im = im.float().to(device)  # 将图像转换为 float 类型并移动到 GPU（或 CPU）
            
            # 随机生成与图像大小相同的噪声
            noise = torch.randn_like(im).to(device)
            
            # 随机采样时间步 t
            t = torch.randint(0, diffusion_config['num_timesteps'], (im.shape[0],)).to(device)
            
            # 根据时间步 t 添加噪声到原始图像
            noisy_im = scheduler.add_noise(im, noise, t)
            
            # 使用模型预测噪声
            noise_pred = model(noisy_im, t)

            # 计算损失，预测的噪声和真实噪声之间的 MSE 损失
            loss = criterion(noise_pred, noise)
            losses.append(loss.item())  # 将损失保存到列表中
            
            # 反向传播并更新模型权重
            loss.backward()
            optimizer.step()
        
        # 打印每个 epoch 结束后的平均损失
        print('Finished epoch:{} | Loss : {:.4f}'.format(
            epoch_idx + 1,
            np.mean(losses),
        ))
        
        # 保存模型权重到检查点文件
        torch.save(model.state_dict(), os.path.join(train_config['task_name'],
                                                    train_config['ckpt_name']))
    
    print('Done Training ...')  # 训练完成


if __name__ == '__main__':
    """
    主函数，解析命令行参数并启动训练。
    """
    parser = argparse.ArgumentParser(description='Arguments for ddpm training')
    parser.add_argument('--config', dest='config_path',  # 配置文件路径参数
                        default='config/default.yaml', type=str)
    args = parser.parse_args()  # 解析命令行参数
    train(args)  # 调用训练函数

9. sample_ddpm.py

import torch
import torchvision
import argparse
import yaml
import os
from torchvision.utils import make_grid  # 用于将多个图像合并成网格
from tqdm import tqdm  # 显示进度条
from models.unet_base import Unet  # 自定义的 UNet 模型
from scheduler.linear_noise_scheduler import LinearNoiseScheduler  # 噪声调度器

# 设置设备为 GPU 或 CPU，根据是否有可用的 CUDA 设备
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')


def sample(model, scheduler, train_config, model_config, diffusion_config):
    """
    根据扩散模型从噪声生成图像，通过一步步地反向生成，最终得到干净的图像。
    每一个时间步都会保存 xt 的预测图像。
    
    :param model: 训练好的 UNet 模型
    :param scheduler: 噪声调度器，用于将噪声添加到图像中
    :param train_config: 训练配置，包括采样数量等
    :param model_config: 模型相关配置，如图像通道、大小等
    :param diffusion_config: 扩散模型的相关配置，包含时间步长等信息
    """
    # 从标准正态分布中生成随机噪声，尺寸为 (样本数, 通道数, 图像大小, 图像大小)
    xt = torch.randn((train_config['num_samples'],
                      model_config['im_channels'],
                      model_config['im_size'],
                      model_config['im_size'])).to(device)
    
    # 反向迭代，逐步从 xt 还原回原始图像 x0
    for i in tqdm(reversed(range(diffusion_config['num_timesteps']))):
        # 预测当前时间步的噪声
        noise_pred = model(xt, torch.as_tensor(i).unsqueeze(0).to(device))
        
        # 使用调度器获得 xt 和 x0 的预测
        xt, x0_pred = scheduler.sample_prev_timestep(xt, noise_pred, torch.as_tensor(i).to(device))
        
        # 保存当前时间步下的图像 x0
        ims = torch.clamp(xt, -1., 1.).detach().cpu()  # 将图像范围限制在 [-1, 1] 之间
        ims = (ims + 1) / 2  # 将图像范围映射到 [0, 1]，适合显示
        grid = make_grid(ims, nrow=train_config['num_grid_rows'])  # 将多个图像按网格排列
        img = torchvision.transforms.ToPILImage()(grid)  # 将 Tensor 转换为 PIL 图像
        
        # 创建 samples 目录以保存生成的图像
        if not os.path.exists(os.path.join(train_config['task_name'], 'samples')):
            os.mkdir(os.path.join(train_config['task_name'], 'samples'))
        
        # 保存图像到文件
        img.save(os.path.join(train_config['task_name'], 'samples', 'x0_{}.png'.format(i)))
        img.close()


def infer(args):
    """
    推理函数，加载模型和配置文件，生成并保存采样图像。
    
    :param args: 从命令行传递的参数，包括配置文件路径
    """
    # 读取配置文件
    with open(args.config_path, 'r') as file:
        try:
            config = yaml.safe_load(file)  # 使用 yaml 加载配置文件
        except yaml.YAMLError as exc:
            print(exc)
    print(config)  # 输出加载的配置信息
    
    # 从配置文件中提取不同模块的参数
    diffusion_config = config['diffusion_params']  # 扩散模型参数
    model_config = config['model_params']  # 模型结构参数
    train_config = config['train_params']  # 训练相关参数
    
    # 加载已训练好的模型权重
    model = Unet(model_config).to(device)
    model.load_state_dict(torch.load(os.path.join(train_config['task_name'],
                                                  train_config['ckpt_name']), map_location=device))
    model.eval()  # 设置模型为推理模式
    
    # 创建噪声调度器
    scheduler = LinearNoiseScheduler(num_timesteps=diffusion_config['num_timesteps'],
                                     beta_start=diffusion_config['beta_start'],
                                     beta_end=diffusion_config['beta_end'])
    
    # 关闭梯度计算以节省资源
    with torch.no_grad():
        sample(model, scheduler, train_config, model_config, diffusion_config)  # 调用采样函数生成图像


if __name__ == '__main__':
    """
    主函数，解析命令行参数并启动推理流程，生成图像。
    """
    parser = argparse.ArgumentParser(description='Arguments for ddpm image generation')  # 创建命令行参数解析器
    parser.add_argument('--config', dest='config_path',  # 配置文件路径
                        default='config/default.yaml', type=str)
    args = parser.parse_args()  # 解析命令行参数
    infer(args)  # 调用推理函数

10. default.yaml

dataset_params:
  im_path: 'data/train/images'

diffusion_params:
  num_timesteps : 1000
  beta_start : 0.0001
  beta_end : 0.02

model_params:
  im_channels : 1
  im_size : 28
  down_channels : [32, 64, 128, 256]
  mid_channels : [256, 256, 128]
  down_sample : [True, True, False]
  time_emb_dim : 128
  num_down_layers : 2
  num_mid_layers : 2
  num_up_layers : 2
  num_heads : 4

train_params:
  task_name: 'default'
  batch_size: 64
  num_epochs: 40
  num_samples : 100
  num_grid_rows : 10
  lr: 0.0001
  ckpt_name: 'ddpm_ckpt.pth'

11. 数据准备

DDPM代码
 VAE代码：

这两个代码都需要下载，需要使用到VAE中处理数据集的代码
Download the csv files for mnist(https://www.kaggle.com/datasets/oddrationale/mnist-in-csv)
这个数据集下载下来是两个csv文件
运行python utils/extract_mnist_images.py生成需要的图片

运行后的目录如下
在这里插入图片描述

然后将data文件夹移动到DDPM中

12. 训练，采样

python -m tools.train_ddpm  用于训练 ddpm
python -m tools.sample_ddpm  用于生成图像

在 DDPM 训练期间，将保存以下输出

在采样期间，将保存以下输出

中所有时间步的采样图像网格task_name/samples/*.png

最终效果，在最后两百步时已经出现了明显的数字

请添加图片描述

五、问题

1. T 为多少时， $x_{T}$ 才服从正态分布

一般情况下T=1000，在下面的公式中，为什么我们希望 ${a_t}$ 接近1且小于1？
$x_t = \sqrt{ 1-a_t} × \mathcal{E}_t + \sqrt{a_t} × x_{t-1}$

原因：
1. 如果 ${a_t}=0$ ，那么 $x_t$ 直接就变成噪声了，我们还是希望上一时刻有所保留，所以不能让 ${a_t}$ 太小
2. 如果 ${a_t}=1$ ，此时 $x_0$ 一直保存
3. 因为 $\overline{a}_t = a_t a_{t-1}a_{t-2} ···a_{2}a_{1}$ ，所以想要 $\overline{a}_t$ 趋近于0，T 要取很大

2. 为什么要令 $a_t = 1-\beta_t$

此时 $\mu^2+\beta^2 = 1$ ，当均值为0时，方差趋近于1，符合问题1中的等式性质

3. 能不能跳步

$P(x_{t-1} | x_{t},x_{0}) = P(x_{t} | x_{t-1},x_{0}) P(x_{t-1} | x_{0}) / P(x_{t} | x_{0})$
在上面的式子中，我们可以利用马尔科夫性质去掉一个 $x_0$ ，即
$P(x_{t-1} | x_{t},x_{0}) = P(x_{t} | x_{t-1}) P(x_{t-1} | x_{0}) / P(x_{t} | x_{0})$
因为用到了马尔科夫，所以就必须一步一步推导

4. 怎么跳步

去马尔科夫，怎么去？在上面的伪代码中，我们其实没有用到 $P(x_{t} | x_{t-1})$ ，所以只要想办法规避到这一项，就能实现跳步

这就是DDIM，DDIM不能称为一个模型，它是一个采样方法

5. 为什么不用UNet直接通过 $x_t$ 预测 $x_{t-1}$

我们为什么要预测 $P(x_{t-1} | x_{t})$ 这个分布而不是预测确切的 $x_{t-1}$ ，这个任务就退化成了分割任务，每个x_{T}对于的同一个x_{0}，就是说取两个一模一样的x_{T}，它一定对于的是同一个x_{0}

6. Variational LB（变分下界）

我们的终极任务hi是拟合 $P(x_{t-1} | x_{t},x_{0})$ 分布

引入这个概念是为了求最大似然估计 $E(\log P(x_0))$ ，在这个式子中加一个负号，即求 $f(loss) = E(-\log P(x_0))$ 最小值，扩散模型最初就是用最大似然估计来定义损失函数的，有通过引入变分下界的方法，得到了一个式子，这个式子可以转换为KL散度

是下面两个P之间的KL散度
$P_{θ}(x_{t-1} | x_{t},x_{0})~~~~~(①)$ （这个是我们预估的）
$P(x_{t-1} | x_{t},x_{0})~~~~~(②$
所以才用①预估②

六、Diffusers 实现 DDPM

1. 训练配置

from dataclasses import dataclass

@dataclass
class TrainingConfig:
    image_size = 64
    train_batch_size = 16
    eval_batch_size = 16
    num_epochs = 50
    gradient_accumulation_steps = 1
    learning_rate = 1e-4
    lr_warmup_steps = 500
    mixed_precision = "fp16"
    output_dir = "ddpm-animefaces-64"
    overwrite_output_dir = True

config = TrainingConfig()

2. 加载数据集

您可以使用Datasets 库加载 Smithsonian Butterflies 数据集：

from datasets import load_dataset

config.dataset_name = "huggan/smithsonian_butterflies_subset"
dataset = load_dataset(config.dataset_name, split="train")

💡 您可以从 HugGan 社区活动中找到其他数据集，也可以通过创建本地 ImageFolder 来使用自己的数据集。如果数据集来自 HugGan 社区活动，或者您使用的是自己的图像，请设置为数据集的存储库 ID。config.dataset_nameimagefolder

数据集使用图像功能自动解码图像数据并将其加载为 PIL。我们可以可视化的图像：

import matplotlib.pyplot as plt

fig, axs = plt.subplots(1, 4, figsize=(16, 4))
for i, image in enumerate(dataset[:4]["image"]):
    axs[i].imshow(image)
    axs[i].set_axis_off()
fig.show()

在这里插入图片描述
不过，图像的大小都不同，因此您需要先对它们进行预处理：

Resize将图像大小更改为中定义的大小。config.image_size
RandomHorizontalFlip通过随机镜像图像来扩充数据集。
Normalize将像素值重新缩放为 [-1， 1] 范围非常重要，这是模型所期望的。

预处理函数：

from torchvision import transforms

preprocess = transforms.Compose(
    [
        transforms.Resize((config.image_size, config.image_size)),
        transforms.RandomHorizontalFlip(),
        transforms.ToTensor(),
        transforms.Normalize([0.5], [0.5]),
    ]
)

使用Datasets 的 set_transform 方法在训练期间动态应用该函数：preprocess

def transform(examples):
    images = [preprocess(image.convert("RGB")) for image in examples["image"]]
    return {"images": images}


dataset.set_transform(transform)

现在，您已准备好将数据集包装在 DataLoader 中进行训练！

import torch

train_dataloader = torch.utils.data.DataLoader(dataset, batch_size=config.train_batch_size, shuffle=True)

3. 创建 UNet2DModel

Diffusers 中的预训练模型可以使用所需的参数从其模型类轻松创建。例如，要创建 UNet2DModel：

from diffusers import UNet2DModel

model = UNet2DModel(
    sample_size=config.image_size,  # the target image resolution
    in_channels=3,  # the number of input channels, 3 for RGB images
    out_channels=3,  # the number of output channels
    layers_per_block=2,  # how many ResNet layers to use per UNet block
    block_out_channels=(128, 128, 256, 256, 512, 512),  # the number of output channels for each UNet block
    down_block_types=(
        "DownBlock2D",  # a regular ResNet downsampling block
        "DownBlock2D",
        "DownBlock2D",
        "DownBlock2D",
        "AttnDownBlock2D",  # a ResNet downsampling block with spatial self-attention
        "DownBlock2D",
    ),
    up_block_types=(
        "UpBlock2D",  # a regular ResNet upsampling block
        "AttnUpBlock2D",  # a ResNet upsampling block with spatial self-attention
        "UpBlock2D",
        "UpBlock2D",
        "UpBlock2D",
        "UpBlock2D",
    ),
)

快速检查样本图像形状与模型输出形状是否匹配

sample_image = dataset[0]["images"].unsqueeze(0)
print("Input shape:", sample_image.shape)
# Input shape: torch.Size([1, 3, 128, 128])
print("Output shape:", model(sample_image, timestep=0).sample.shape)
# Output shape: torch.Size([1, 3, 128, 128])

4. 创建调度程序

调度程序的行为会有所不同，具体取决于您是使用模型进行训练还是推理。在推理过程中，调度程序从噪声中生成图像。在训练期间，调度程序从扩散过程中的特定点获取模型输出或样本，并根据噪声计划和更新规则将噪声应用于图像。

让我们看一下 DDPMScheduler 并使用该方法向之前的 API 添加一些随机噪声：add_noisesample_image

import torch
from PIL import Image
from diffusers import DDPMScheduler

noise_scheduler = DDPMScheduler(num_train_timesteps=1000)
noise = torch.randn(sample_image.shape)
timesteps = torch.LongTensor([50])
noisy_image = noise_scheduler.add_noise(sample_image, noise, timesteps)

Image.fromarray(((noisy_image.permute(0, 2, 3, 1) + 1.0) * 127.5).type(torch.uint8).numpy()[0])

查看这一步的输出（看完之后注释掉下面的，）：

# Denormalize and convert to PIL for display
def denormalize(tensor):
    tensor = tensor * 0.5 + 0.5  # reverse normalization
    return torch.clamp(tensor, 0, 1)

# Denormalize the noisy image
denormalized_image = denormalize(noisy_image)
image = Image.fromarray((denormalized_image.squeeze(0).permute(1, 2, 0) * 255).byte().numpy())
image.show()

在这里插入图片描述
该模型的训练目标是预测添加到图像中的噪声。此步骤的损失可以通过以下方式计算：

import torch.nn.functional as F

noise_pred = model(noisy_image, timesteps).sample
loss = F.mse_loss(noise_pred, noise)

5. 训练模型

到目前为止，您已经完成了开始训练模型的大部分工作，剩下的就是把所有东西放在一起。

首先，您需要一个优化器和一个学习率调度器：

from diffusers.optimization import get_cosine_schedule_with_warmup

optimizer = torch.optim.AdamW(model.parameters(), lr=config.learning_rate)
lr_scheduler = get_cosine_schedule_with_warmup(
    optimizer=optimizer,
    num_warmup_steps=config.lr_warmup_steps,
    num_training_steps=(len(train_dataloader) * config.num_epochs),
)

然后，您需要一种方法来评估模型。为了进行评估，您可以使用 DDPMPipeline 生成一批示例图像并将其保存为网格：

from diffusers import DDPMPipeline
from diffusers.utils import make_image_grid
import os

def evaluate(config, epoch, pipeline):
    # Sample some images from random noise (this is the backward diffusion process).
    # The default pipeline output type is `List[PIL.Image]`
    images = pipeline(
        batch_size=config.eval_batch_size,
        generator=torch.Generator(device='cpu').manual_seed(config.seed), # Use a separate torch generator to avoid rewinding the random state of the main training loop
    ).images

    # Make a grid out of the images
    image_grid = make_image_grid(images, rows=4, cols=4)

    # Save the images
    test_dir = os.path.join(config.output_dir, "samples")
    os.makedirs(test_dir, exist_ok=True)
    image_grid.save(f"{test_dir}/{epoch:04d}.png")

该函数用于模型的中期评估，从噪声生成图像样本，将这些样本保存为网格图像，方便查看模型在各个训练阶段的生成效果。

6. 核心代码

前边的三个部分分别配置了一些训练参数，以及训练数据和模型，这些都是比较工程化的部分，而我们在上面推导的 DDPM 核心算法还没有实现。在这一小节我们主要来实现核心的算法。

首先我们需要先定义 $\beta、\alpha$ ，以及 $\bar\alpha$ 等最基本的常量，这里我们保持 DDPM 原论文的配置，也就是 $\beta$ 初始为 $1\times10^{-4}$ ，最终为 0.02 0.020.02，且共有 1000个时间步：

import torch

class DDPM:
    def __init__(
        self,
        num_train_timesteps:int = 1000,
        beta_start: float = 0.0001,
        beta_end: float = 0.02,
    ):
        self.betas = torch.linspace(beta_start, beta_end, num_train_timesteps, dtype=torch.float32)
        self.alphas = 1.0 - self.betas
        self.alphas_cumprod = torch.cumprod(self.alphas, dim=0)
        self.timesteps = torch.arange(num_train_timesteps - 1, -1, -1)

然后是比较简单的前向过程，只需要实现加噪即可，按照 $x_t =\sqrt{1 - \overline{a}_t} × \mathcal{E} + \sqrt{\overline{a}_t}x_{0}$ 这个公式实现即可。注意需要将系数的维度数量都与输入样本对齐：

class DDPM:
    ...
    
    def add_noise(
        self,
        original_samples: torch.Tensor,
        noise: torch.Tensor,
        timesteps: torch.Tensor,
    ):
        alphas_cumprod = self.alphas_cumprod.to(device=original_samples.device ,dtype=original_samples.dtype)
        noise = noise.to(original_samples.device)
        timesteps = timesteps.to(original_samples.device)

        # \sqrt{\bar\alpha_t}
        sqrt_alpha_prod = alphas_cumprod[timesteps].flatten() ** 0.5
        while len(sqrt_alpha_prod.shape) < len(original_samples.shape):
            sqrt_alpha_prod = sqrt_alpha_prod.unsqueeze(-1)
        
        # \sqrt{1 - \bar\alpha_t}
        sqrt_one_minus_alpha_prod = (1.0 - alphas_cumprod[timesteps]).flatten() ** 0.5
        while len(sqrt_one_minus_alpha_prod.shape) < len(original_samples.shape):
            sqrt_one_minus_alpha_prod = sqrt_one_minus_alpha_prod.unsqueeze(-1)
        
        return sqrt_alpha_prod * original_samples + sqrt_one_minus_alpha_prod * noise

反向过程相对来说比较复杂，不过因为我们已经完成了公式的推导，只需要按照公式实现即可。我们也再把公式贴到这里，对着公式实现具体的代码：
$\sigma = (\frac{\alpha_t}{\beta_t} + \frac{1}{1-\overline{a}_{t-1}})^{-\frac{1}{2}}$ $\mu= \frac{1}{\sqrt{\alpha_t}}(x_t + \frac{1-\alpha_t}{\sqrt{1-\overline{a}_{t}}})ε_t'$

class DDPM:
    ...

    @torch.no_grad()
    def sample(
        self,
        unet: UNet2DModel,
        batch_size: int,
        in_channels: int,
        sample_size: int,
    ):
        betas = self.betas.to(unet.device)
        alphas = self.alphas.to(unet.device)
        alphas_cumprod = self.alphas_cumprod.to(unet.device)
        timesteps = self.timesteps.to(unet.device)
        images = torch.randn((batch_size, in_channels, sample_size, sample_size), device=unet.device)
        for timestep in tqdm(timesteps, desc='Sampling'):
            pred_noise: torch.Tensor = unet(images, timestep).sample

            # mean of q(x_{t-1}|x_t)
            alpha_t = alphas[timestep]
            alpha_cumprod_t = alphas_cumprod[timestep]
            sqrt_alpha_t = alpha_t ** 0.5
            one_minus_alpha_t = 1.0 - alpha_t
            sqrt_one_minus_alpha_cumprod_t = (1 - alpha_cumprod_t) ** 0.5
            mean = (images - one_minus_alpha_t / sqrt_one_minus_alpha_cumprod_t * pred_noise) / sqrt_alpha_t
            
            # variance of q(x_{t-1}|x_t)
            if timestep > 0:
                beta_t = betas[timestep]
                one_minus_alpha_cumprod_t_minus_one = 1.0 - alphas_cumprod[timestep - 1]
                one_divided_by_sigma_square = alpha_t / beta_t + 1.0 / one_minus_alpha_cumprod_t_minus_one
                variance = (1.0 / one_divided_by_sigma_square) ** 0.5
            else:
                variance = torch.zeros_like(timestep)
            
            epsilon = torch.randn_like(images)
            images = mean + variance * epsilon
        images = (images / 2.0 + 0.5).clamp(0, 1).cpu().permute(0, 2, 3, 1).numpy()
        return images

7. 训练与推理

最后是训练和推理的代码，这部分也比较工程，直接套用现成代码即可：

from accelerate import Accelerator
from diffusers.optimization import get_cosine_schedule_with_warmup
from diffusers.utils import make_image_grid, numpy_to_pil
import torch.nn.functional as F
import os

model = model.cuda()
ddpm = DDPM()
optimizer = torch.optim.AdamW(model.parameters(), lr=config.learning_rate)
lr_scheduler = get_cosine_schedule_with_warmup(
    optimizer=optimizer,
    num_warmup_steps=config.lr_warmup_steps,
    num_training_steps=(len(dataloader) * config.num_epochs),
)
accelerator = Accelerator(
    mixed_precision=config.mixed_precision,
    gradient_accumulation_steps=config.gradient_accumulation_steps,
    log_with="tensorboard",
    project_dir=os.path.join(config.output_dir, "logs"),
)
model, optimizer, dataloader, lr_scheduler = accelerator.prepare(
    model, optimizer, dataloader, lr_scheduler
)
global_step = 0
for epoch in range(config.num_epochs):
    progress_bar = tqdm(total=len(dataloader), disable=not accelerator.is_local_main_process, desc=f'Epoch {epoch}')

    for step, batch in enumerate(dataloader):
        clean_images = batch["images"]
        # Sample noise to add to the images
        noise = torch.randn(clean_images.shape, device=clean_images.device)
        bs = clean_images.shape[0]
        # Sample a random timestep for each image
        timesteps = torch.randint(
            0, ddpm.num_train_timesteps, (bs,), device=clean_images.device,
            dtype=torch.int64
        )
        # Add noise to the clean images according to the noise magnitude at each timestep
        noisy_images = ddpm.add_noise(clean_images, noise, timesteps)
        with accelerator.accumulate(model):
            # Predict the noise residual
            noise_pred = model(noisy_images, timesteps, return_dict=False)[0]
            loss = F.mse_loss(noise_pred, noise)
            accelerator.backward(loss)
            accelerator.clip_grad_norm_(model.parameters(), 1.0)
            optimizer.step()
            lr_scheduler.step()
            optimizer.zero_grad()
        progress_bar.update(1)
        logs = {"loss": loss.detach().item(), "lr": lr_scheduler.get_last_lr()[0], "step": global_step}
        progress_bar.set_postfix(**logs)
        accelerator.log(logs, step=global_step)
        global_step += 1

    if accelerator.is_main_process:
        # evaluate
        images = ddpm.sample(model, config.eval_batch_size, 3, config.image_size)
        image_grid = make_image_grid(numpy_to_pil(images), rows=4, cols=4)
        samples_dir = os.path.join(config.output_dir, 'samples')
        os.makedirs(samples_dir, exist_ok=True)
        image_grid.save(os.path.join(samples_dir, f'{global_step}.png'))
        # save models
        model.save_pretrained(config.output_dir)