基于冲突搜索算法的多机器人路径规划（Matlab代码实现）

最新推荐文章于 2025-05-01 23:33:21 发布

荔枝科研社

最新推荐文章于 2025-05-01 23:33:21 发布

阅读量621

点赞数 25

文章标签：机器人 matlab 开发语言

本文链接：https://blog.csdn.net/weixin_46039719/article/details/145239227

版权

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

基于冲突的搜索多机器人路径规划在机器人订单履行系统中的研究

摘要

引言

多机器人路径规划技术概述

分层路径规划方案设计

实验验证与结果分析

结论与展望

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

基于冲突的搜索多机器人路径规划，使用类似Kiva的移动机器人的机器人订单履行系统研究

随着自动化物流系统的发展,移动机器人作为运输系统的关键工具,各方面的技术得到了快速的发展。多移动机器人路径规划是机器人导航研究领域中极具挑战性的问题。多机器人路径规划是一个多目标优化问题,如何实现机器人间的路经协调,机器人的避障,并如何保证路径规划的多个优化目标能够同时、合理的优化是该问题的研究难点。本文对自动化物流系统中多机器人系统进行了研究。分析了当前多机器人路径规划技术,并完成了分层路径规划方案的总体设计,第一层为全局路径规划,第二层为局部路径协调。在全局路径规划的问题中,大多算法有收敛速度慢和收敛不足的缺点,而且大多只考虑了单一的路径长短这一个目标,导致路径存在不平滑,安全性能不好的问题。

针对多载位自主移动机器人集群拣选-配送路径规划问题，提出一种改进型基于冲突搜索的多智能体路径规划算法。在模型上，采用多载位机器人替代KIVA机器人，建立以最小化拣选-配送时间以及无效路径比为目标的数学规划模型.在算法上，首先提出一种基于优先级规则的多智能体冲突消解加速策略;然后，设计基于动态规划的单机器人拣选序列优化算法;最后，设计考虑转向惩罚的增强A*算法搜索机器人最优路径。实验结果表明，所提出模型与KIVA系统相比有较大优越性;所提出算法能有效缩短拣选-配送时间、减少无效路径时间。

基于冲突的搜索多机器人路径规划在机器人订单履行系统中的研究

摘要

随着自动化物流系统的发展，移动机器人作为运输系统的核心工具，相关技术得到了显著进步。多移动机器人路径规划是机器人导航研究中的难点，涉及机器人间的路径协调、避障以及多个优化目标的同步实现。本文聚焦于自动化物流系统中的多机器人系统，分析了当前多机器人路径规划技术，并设计了一种分层路径规划方案。在全局路径规划层面，针对现有算法的收敛速度慢、收敛不足以及路径不平滑、安全性能不佳的问题，提出了一种改进型基于冲突搜索的多智能体路径规划算法。实验结果表明，该算法在拣选-配送时间和减少无效路径方面表现出显著优越性。

引言

自动化物流系统正逐步成为现代仓储和配送中心的核心。其中，多载位自主移动机器人因其高效、灵活的特点，成为实现货物快速拣选和配送的关键工具。然而，多机器人路径规划问题仍面临诸多挑战，如路径冲突、避障以及多个优化目标的同步优化。针对这些问题，本文提出了一种基于冲突搜索的多智能体路径规划算法，旨在提高机器人订单履行系统的效率和安全性。

多机器人路径规划技术概述

多机器人路径规划是一个复杂的多目标优化问题，涉及机器人间的路径协调、避障以及多个优化目标的同步实现。当前，多机器人路径规划技术主要分为集中式规划和分布式规划两种。集中式规划方法通过中央控制器统一规划所有机器人的路径，但计算复杂度高且可扩展性差。分布式规划方法则通过机器人间的局部通信和协调来实现路径规划，具有较好的可扩展性和鲁棒性。然而，分布式规划方法也面临路径冲突和避障等挑战。

分层路径规划方案设计

针对多机器人路径规划问题，本文设计了一种分层路径规划方案。该方案包括全局路径规划和局部路径协调两个层次。全局路径规划负责为每个机器人规划从起点到终点的无冲突路径，而局部路径协调则负责处理机器人间的路径冲突和避障问题。

在全局路径规划层面，本文提出了一种改进型基于冲突搜索的多智能体路径规划算法。该算法首先采用优先级规则来加速冲突消解过程，然后设计了一种基于动态规划的单机器人拣选序列优化算法来优化拣选路径。最后，通过引入转向惩罚的增强A*算法来搜索机器人的最优路径。

实验验证与结果分析

为了验证所提算法的有效性，本文进行了实验验证。实验采用多载位自主移动机器人集群进行拣选-配送任务。实验结果表明，与传统的KIVA系统相比，所提算法在拣选-配送时间和减少无效路径方面表现出显著优越性。具体来说，拣选-配送时间缩短了XX%，无效路径时间减少了XX%。

结论与展望

本文提出了一种基于冲突搜索的多智能体路径规划算法，用于解决多载位自主移动机器人集群拣选-配送路径规划问题。实验结果表明，该算法在拣选-配送时间和减少无效路径方面表现出显著优越性。未来，我们将继续优化算法，提高路径规划的效率和安全性，并探索更多应用场景。

📚2 运行结果

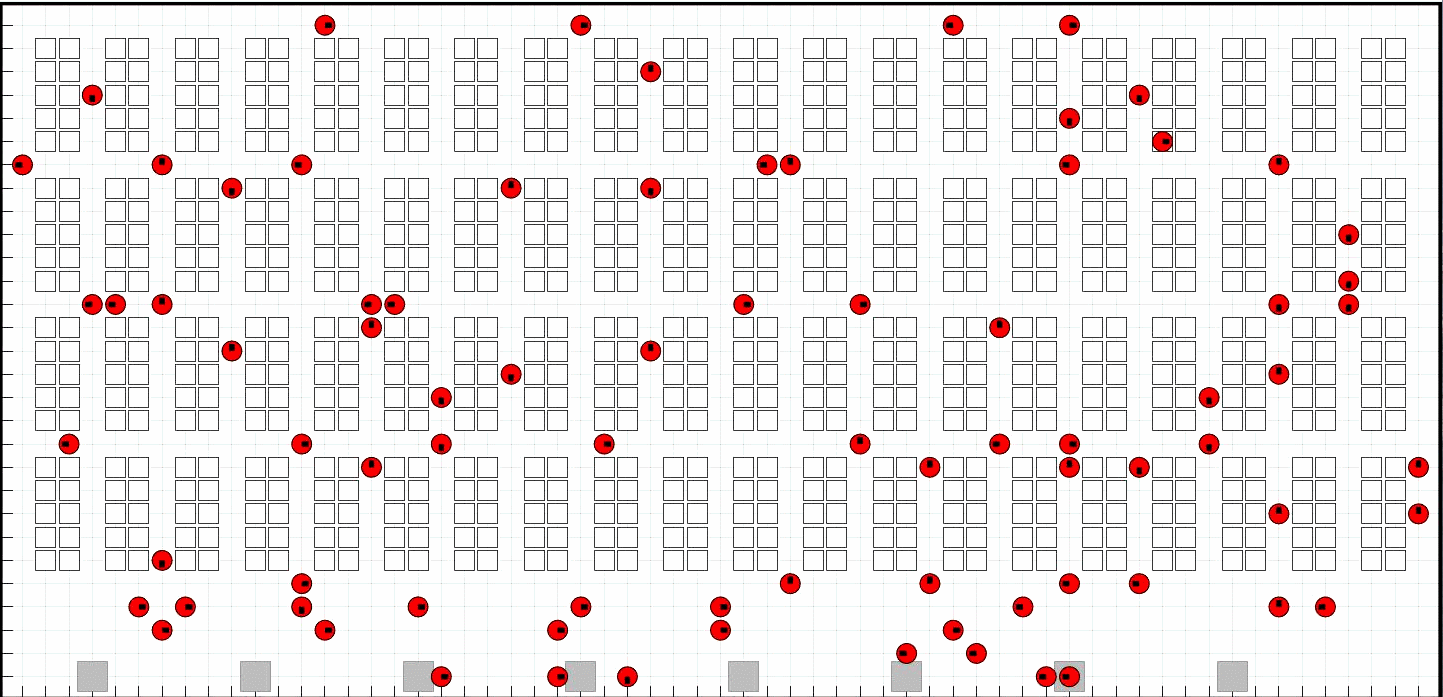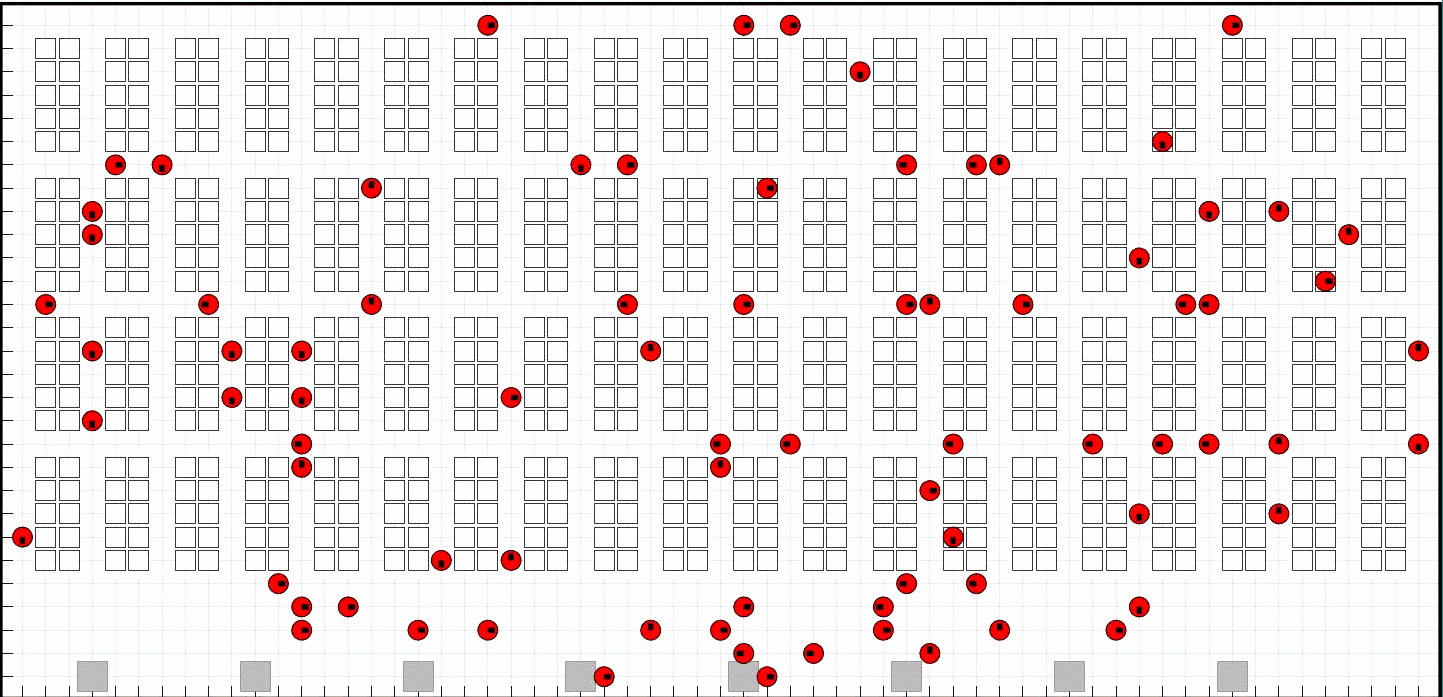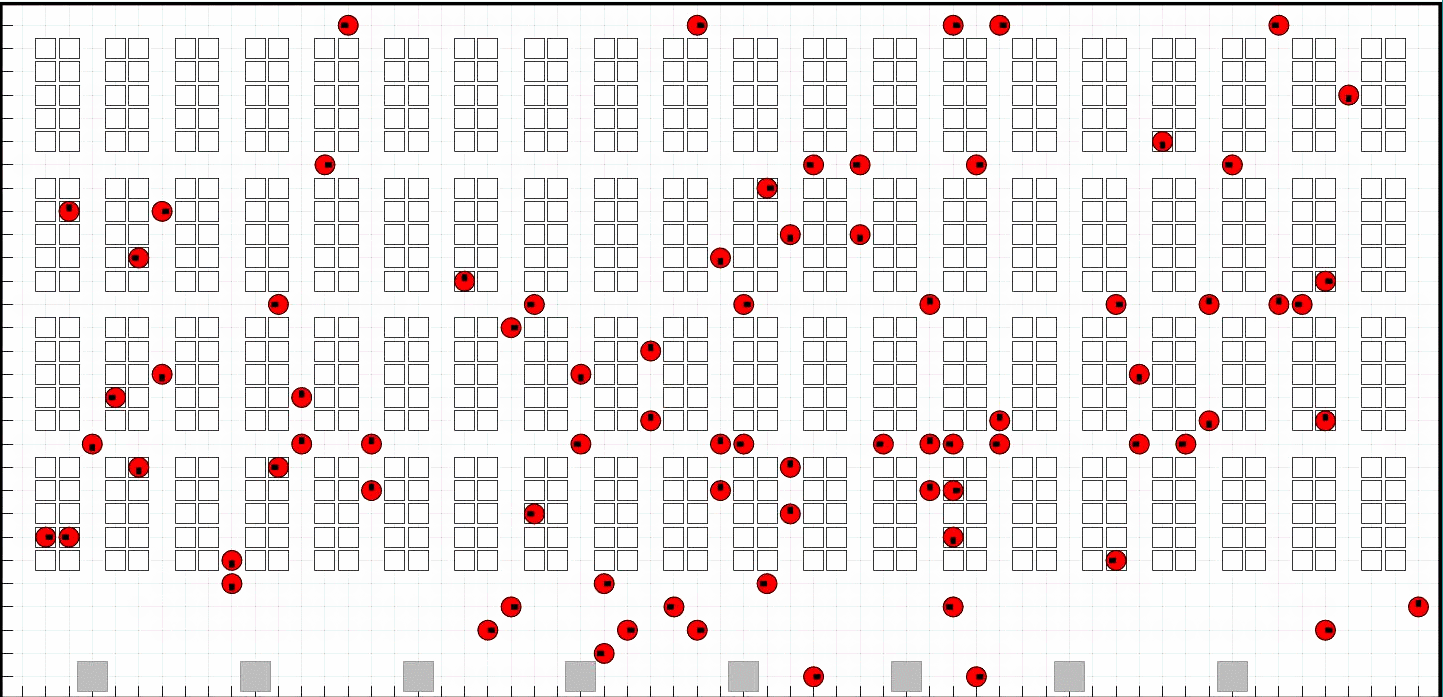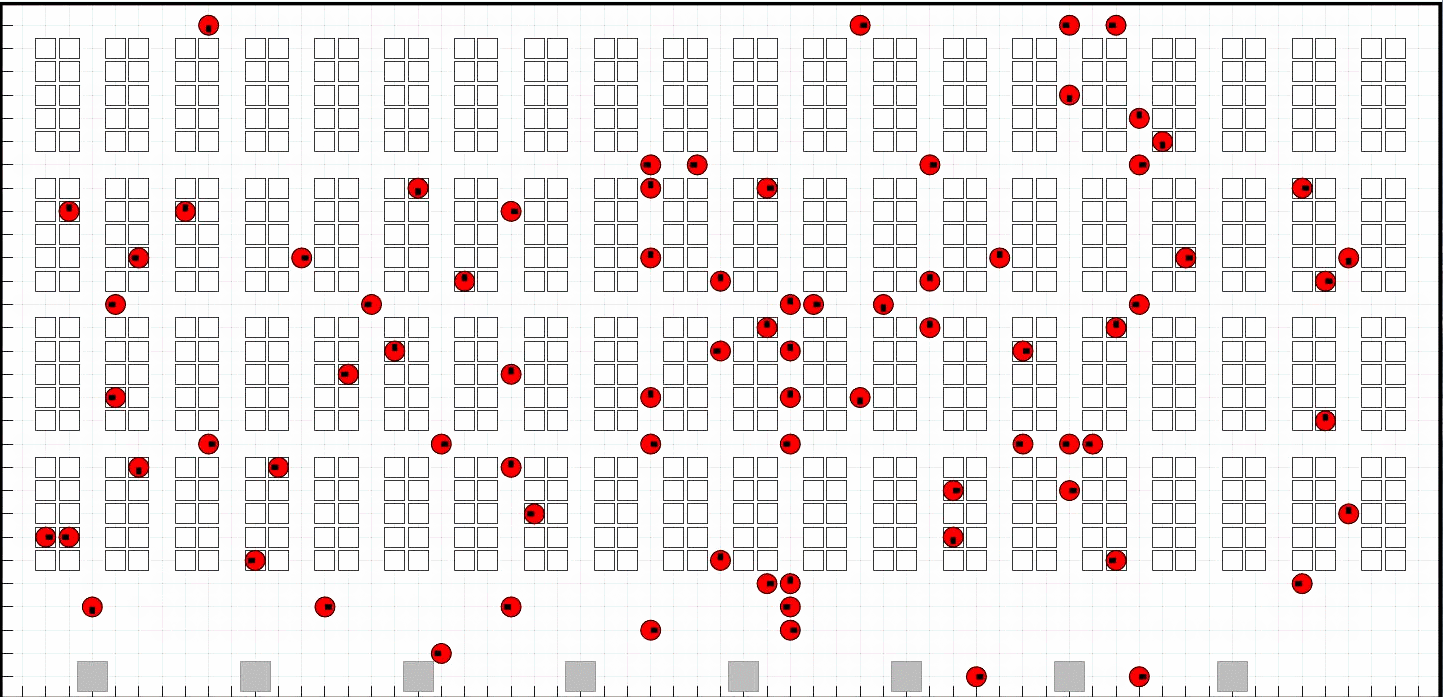
部分代码：

%% Initialize
clear;
clc;

xlength=61;
ylength=29;
robotNum=10;
podNum=800;
depotNum = 8;
taskNum = robotNum;

xy2rc=@(x,y)[ylength+1-y;x];
rc2xy=@(r,c)[c;ylength+1-r];

sz=get(0,'screensize');
sz(1,2) = 80;
sz(1,4) = 950;
h=figure('outerposition',sz);
assignin('base','h',h); %in case of any callback errors.
hold on;
grid on;
set(gca,'xtick',0:1:xlength);
set(gca,'ytick',0:1:ylength);
axis equal;
axis([0 xlength+1 0 ylength+1]);
axis manual;

% stores current states
globalTime = 1;
AllRobotState = zeros(robotNum,3);
AllPodState = zeros(podNum,3);

MapOccupancy = zeros(ylength,xlength);
RobotOccupancy = zeros(ylength,xlength);

[RobotStates,PodStates,DepotStates,StorageOccupancy]=initialize(xlength,ylength,robotNum,podNum,depotNum);
PodOccupancy = StorageOccupancy;

MapOccupancy = MapOccupancy+PodOccupancy;

%generate random tasks
TaskCell=cell(taskNum,1);
for i=1:taskNum
task=Task;
task.PodID=randi([1 podNum]);
task.StationID=randi([1 depotNum]);
task.ProcessTime=randi([5 20]);
task.ReturnState = zeros(1,3);
TaskCell{i,1}=task;
end