【二维盖板驱动空腔流求解器】使用涡量-流函数公式解决盖驱动腔流问题（Matlab代码实现）

最新推荐文章于 2025-05-09 20:23:30 发布

荔枝科研社

最新推荐文章于 2025-05-09 20:23:30 发布

阅读量451

点赞数 23

文章标签： matlab 线性代数概率论

本文链接：https://blog.csdn.net/weixin_46039719/article/details/147806408

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

基于涡量-流函数公式的二维盖板驱动空腔流求解器研究

一、基本原理与数学表达

二、二维盖板驱动空腔流的标准问题定义

三、数值方法实现

四、适用性分析与局限性

五、研究现状与典型案例

六、结论与展望

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

基于涡量-流函数公式的二维盖板驱动空腔流求解器研究

一、基本原理与数学表达

涡量-流函数法的核心思想
通过将原始变量（速度 u,vu,v 和压力 pp）转换为导出变量 涡量 ωω 和 流函数 ψψ ，消去压力项，简化不可压缩Navier-Stokes方程的求解。该方法尤其适用于二维不可压缩流动，因连续性方程自动满足。
数学定义与方程
- 涡量：定义为速度场的旋度，二维下为标量：
- 流函数：与速度场的关系为：

由此可得流函数的泊松方程：
∇2ψ=−ω

涡量输运方程（由动量方程推导）：

其中 Re为雷诺数，体现惯性力与粘性力的相对重要性。

边界条件特性
流函数在固壁边界处为常数（通常设为零），而涡量在固壁处需通过速度梯度确定，例如采用泰勒展开或迭代法。

二、二维盖板驱动空腔流的标准问题定义

几何与边界条件
- 几何：正方形腔体（边长 L=1L=1），顶部盖板以速度 u=1u=1 水平移动，其余三边静止（无滑移条件）。
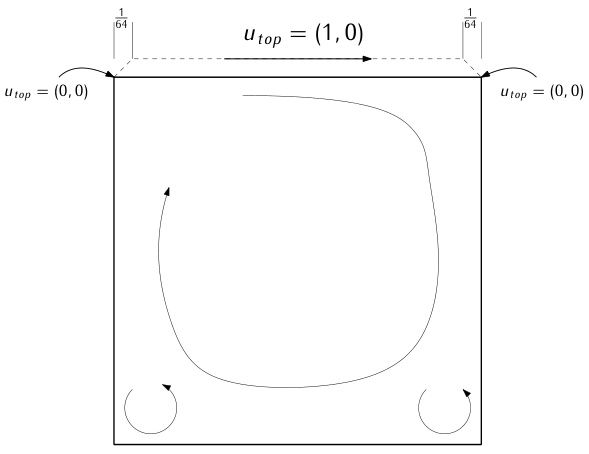
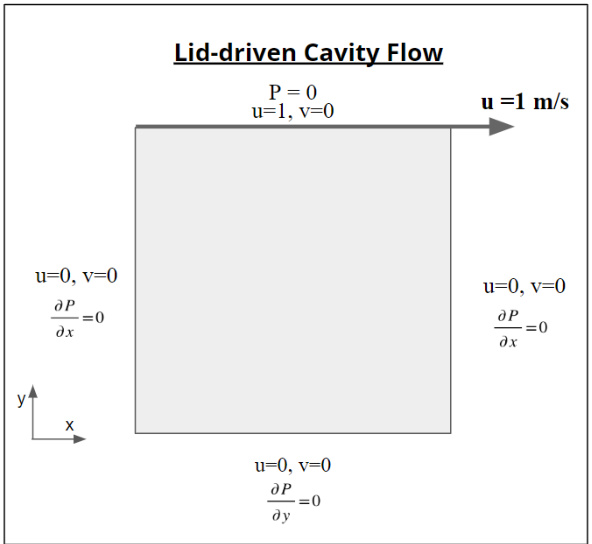
- 边界条件：

典型流动现象
- 低雷诺数时形成单一主涡；
- 高雷诺数（如 Re>1000）时出现次级涡、三次涡，甚至四元涡结构。

三、数值方法实现

离散策略
- 有限差分法：空间导数采用中心差分（二阶精度），时间离散可选显式Euler或隐式Crank-Nicolson格式以提高稳定性。
- 高阶格式：如四阶Hermitian插值用于速度项，四阶中心差分用于对流项，提升精度。
边界条件处理
- 流函数：固壁处 ψ=0ψ=0；
- 涡量：利用壁面速度梯度计算，例如通过泰勒展开：
求解流程
1. 初始化流场（ψ,ω）；
2. 迭代求解泊松方程 ∇2ψ=−ω；
3. 更新涡量方程；
4. 检查收敛性（残差<10−10）。

四、适用性分析与局限性

优势
- 自动满足连续性方程，无需压力-速度耦合；
- 二维问题中计算效率高，仅需两方程联立。
局限性
- 三维扩展困难：因流函数在三维中退化为矢量势，方程复杂度显著增加；
- 涡量边界条件敏感性：壁面涡量计算易引入误差，需高精度离散。

五、研究现状与典型案例

高精度算法
- 谱方法：解耦涡量与流函数，通过类泊松方程高效求解，适用于复杂几何。
- 小波方法：结合自适应网格，捕捉高雷诺数下的精细涡结构。
典型应用案例
- 高雷诺数腔流：Erturk等人采用601×601网格，计算至Re=21,000，发现新四元涡结构。
- 非均匀网格优化：Mao等人通过变网格技术提升壁面附近分辨率，准确捕捉反转流。
- 圆柱起动涡模拟：改进ADI迭代方法，成功模拟涡旋周期性脱落。

六、结论与展望

涡量-流函数法在二维不可压缩流动中展现出色效率与精度，尤其在盖板驱动腔流等经典问题中成为验证算法的基准。未来研究方向包括：

开发三维扩展算法；
结合机器学习优化网格与迭代过程；
探索更高雷诺数下的湍流模拟。

📚2 运行结果

部分代码：

%%% CREATE VELOCITY FROM STREAM FUNCTION
u(2:Nx-1,Ny) = Wall_Velocity;
u(i,j) = (St(i,jp)-St(i,jm))/(2*h); v(i,j) = (-St(ip,j)+St(im,j))/(2*h);
%%% PLOTS
cm = hsv(ceil(100/0.7)); cm = flipud(cm(1:100,:));
figure(1); contourf(x,y,u',23,'LineColor','none');
title('U-velocity'); xlabel('x-location'); ylabel('y-location')
axis('equal',[0 L 0 L]); colormap(cm); colorbar('westoutside');
figure(2); plot(y,u(round(Ny/2),:));
title('Centerline x-direction velocity');
xlabel('y/L'); ylabel('u/U'); axis('square'); xlim([0 L]); grid on
N = 1000; xstart = max(x)*rand(N,1); ystart = max(y)*rand(N,1);
[X,Y] = meshgrid(x,y);
figure(3); h=streamline(X,Y,u',v',xstart,ystart,[0.1, 200]);
title('Stream Function'); xlabel('x-location'); ylabel('y-location')
axis('equal',[0 L 0 L]); set(h,'color','k')