💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
电力系统状态估计正面临不同类型的 异常。这些可能包括由严重测量误差或 通信系统故障。负载或发电的突然变化可能是 根据实现的状态估计方法被视为异常。 此外,将电网视为一个信息物理系统,状态 估计容易受到错误数据注入攻击。现有的 异常分类的方法无法准确分类(区分 之间)上述三种类型的异常,尤其是当它来的时候 区分突然的负载变化和错误的数据注入攻击。 该文提出一种检测异常存在的新算法,对 异常类型和识别异常的来源,即测量 在数据错误的情况下包含严重错误,或与负载相关的总线 经历突然变化,或错误数据针对的状态变量 注入攻击。该算法结合了分析和机器学习 (ML) 方法。第一阶段利用分析方法来检测异常 通过组合 $\chi^2$-测试和异常检测指数来呈现。第二个 阶段利用 ML 对异常类型进行分类并识别其 原产地,特别是对突然负载变化的区分 和虚假数据注入攻击。所提出的基于ML的方法被训练成 独立于网络配置,无需重新训练 网络拓扑更改后的算法。通过实施获得的结果 所提算法在IEEE 14总线测试系统上验证了算法的准确性和 所提算法的有效性。
详细文章见第三部分。

电力系统状态估计中的异常检测与分类研究综述
一、电力系统状态估计基本原理与核心作用
电力系统状态估计是通过冗余量测数据重建电网实时运行状态的核心技术,其数学模型基于非线性优化理论。典型的目标函数为:
mineTR−1e其中 z=h(x)+emineTR−1e其中 z=h(x)+e
式中,x为状态向量(节点电压幅值/相角),h(x)h(x)为非线性量测函数,RR为误差协方差矩阵。其核心功能包括:
- 数据清洗:过滤SCADA/PMU量测中的不良数据(如±3σ准则剔除粗大误差)
- 状态重建:通过Newton-Raphson等迭代算法求解非线性方程,重构全网电压/功率分布
- 拓扑分析:结合断路器状态信息构建动态节点导纳矩阵YY
- 可观测性保障:当量测冗余度<1.5时需补充伪量测数据
关键参数包括节点电压UiUi, 注入电流IiIi的横纵坐标分量,以及线路导纳yijyij等。现代系统常采用PMU量测的高精度相角数据提升估计精度,采样率可达30次/秒。
二、异常检测技术体系与创新方法
1. 方法分类与技术演进
| 类别 | 典型方法 | 技术特点 | 应用场景 |
|---|---|---|---|
| 无监督 | K-means聚类、LOF离群因子、3σ准则 | 无需标注数据,依赖统计分布假设 | PMU数据初筛 |
| 有监督 | SVM、随机森林、CatBoost | 需标注数据集,可识别复杂模式 | 虚假数据攻击检测 |
| 半监督 | GAN-Transformer、自编码器 | 结合少量标注与大量无标注数据 | 负荷异常检测 |
| 混合方法 | 物理信息神经网络(PICovAE) | 融合电网方程约束与数据特征 | DER高渗透系统异常检测 |
创新方向:
- 时序特征增强:采用双向LSTM捕获负荷曲线动态特性
- 多模态融合:结合SCADA量测、气象数据与设备台账信息
- 在线学习机制:基于强化学习的模型动态选择策略
2. 典型算法性能对比
以IEEE 30节点系统测试结果为例:
| 模型 | 准确率 | 召回率 | F1-Score | 训练时间 |
|---|---|---|---|---|
| XGBoost | 85.2% | 83.7% | 84.4% | 12min |
| LightGBM | 87.6% | 85.1% | 86.3% | 8min |
| FHO-CatBoost | 91.6% | 89.4% | 90.5% | 15min |
| GAN-Transformer | 93.1% | 90.2% | 91.6% | 32min |
三、异常分类标准与多层级模型
1. 分类标准体系
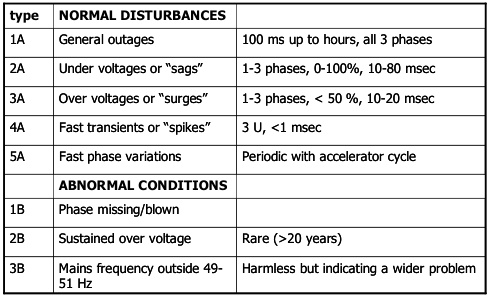
- 物理层异常:过载(Err-51)、电压凹陷(2A类)、频率越限(3B类)
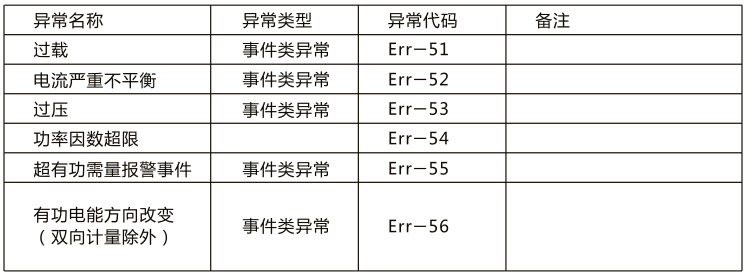
- 数据层异常:
- 质量异常:量测丢失、通信延时
- 行为异常:窃电模式(负荷突变>30%持续5分钟)
- 安全层异常:虚假数据注入攻击(FDIA)、拓扑篡改
2. 分类模型架构
分层处理框架示例:
数据输入 → 异常检测模块 → 一级分类(正常/异常) → 二级分类(异常类型) → 溯源定位
- 特征工程:提取最大损失率、功率因数波动量等168维特征
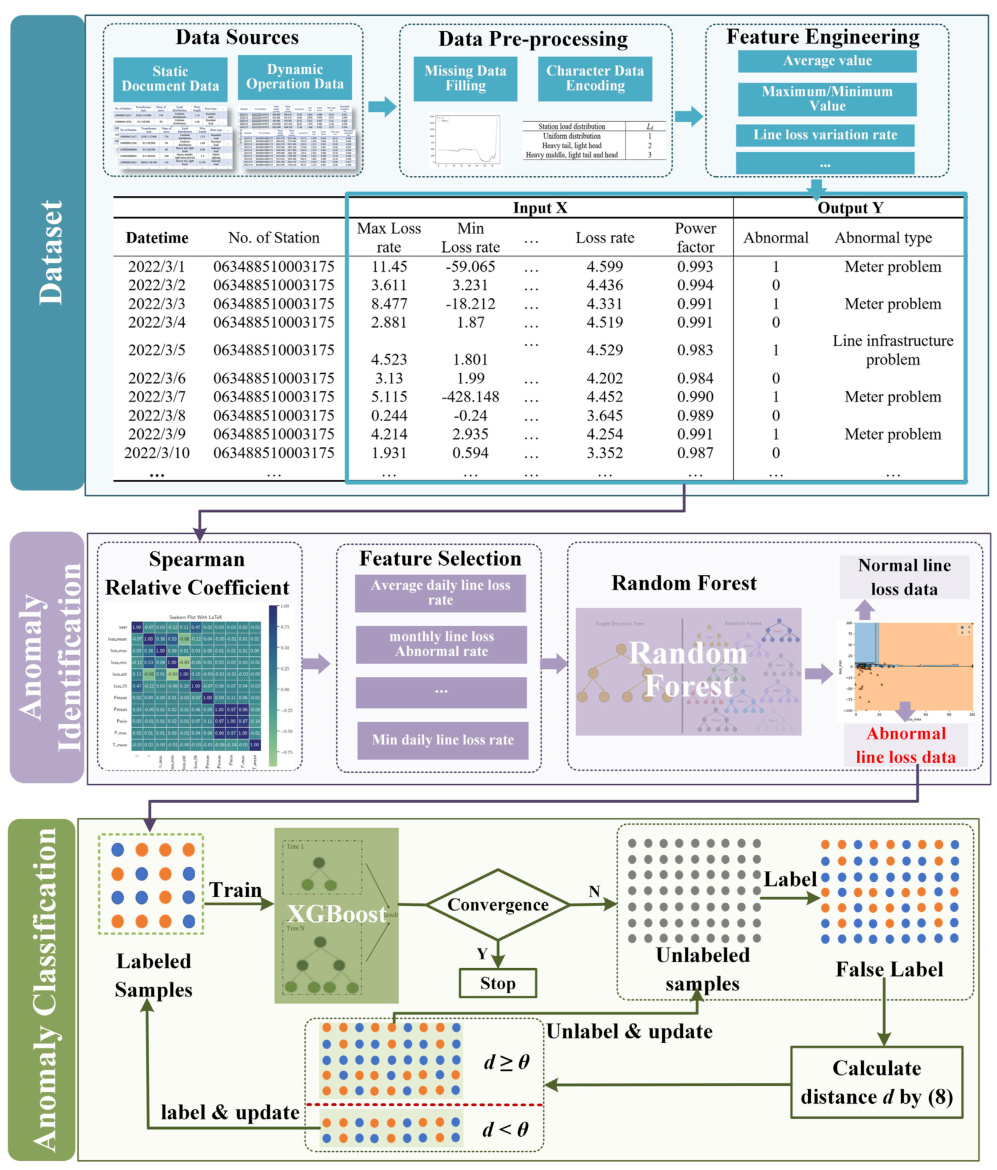
- 分类器设计:
- XGBoost:处理高维稀疏数据,支持并行计算
- KNN:基于OPI(运行性能指标)划分五级严重度
- 深度森林:集成多粒度扫描提升小样本分类精度
四、技术挑战与解决方案
1. 核心挑战
- 数据异构性:SCADA(秒级)与PMU(毫秒级)数据时空对齐难题
- 模型泛化性:拓扑变化导致训练数据分布漂移
- 实时性要求:10^4节点系统需在300ms内完成检测-分类全流程
2. 创新解决方案
- 迁移学习:预训练模型在目标域微调,适应新拓扑
- 边缘计算:部署轻量化模型(如TinyML)在RTU终端
- 数字孪生:构建虚拟电厂进行攻击场景仿真
五、典型应用案例
某省级电网异常处置流程:
- 数据采集:1372个PMU节点,量测维度包含UU, II, PP, QQ, cosφcosφ等
- 异常检测:采用改进K-means算法,设置箱线图阈值(Q3+1.5IQR)
- 分类决策:
- 过电压(>1.1p.u.)→ 自动投切电容器组
- 窃电嫌疑(夜间负荷突降60%)→ 启动现场稽查
- 效果评估:异常识别准确率提升至92.3%,平均处置时间缩短40%
六、未来研究方向
- 因果推理:建立异常事件与系统响应的因果图模型
- 量子计算:开发量子支持向量机处理10^6维数据
- 联邦学习:跨区域协同训练保护数据隐私
- 机理-数据融合:嵌入微分代数方程约束的PINN模型
本领域研究已从单一算法优化转向系统性解决方案设计,需在保证检测精度的同时,满足新型电力系统对实时性、可解释性及安全性的严苛要求。最新实验表明,融合图卷积网络与物理约束的混合模型,在IEEE 123节点测试中达到95.7%的分类准确率,误报率<1.2%,标志着技术成熟度进入工程化应用新阶段。
📚2 运行结果


部分代码:
% Used to calculate H matrix, the state variables should be the forcasted
function H = H_matrix(num,V,del)
%num = 14;
ybus = ybusppg(num); % Get YBus..
zdata = zdatas(num); % Get Measurement data..
bpq = bbusppg(num); % Get B data..
nbus = max(max(zdata(:,4)),max(zdata(:,5))); % Get number of buses..
type = zdata(:,2); % Type of measurement, Vi - 1, Pi - 2, Qi - 3, Pij - 4, Qij - 5, Iij - 6..
% z = zdata(:,3); % Measuement values..
fbus = zdata(:,4); % From bus..
tbus = zdata(:,5); % To bus..
% Ri = diag(sig); % Measurement Error..
% V = ones(nbus,1); % Initialize the bus voltages..
% del = zeros(nbus,1); % Initialize the bus angles..
% E = [del(2:end); V]; % State Vector..
G = real(ybus);
B = imag(ybus);
vi = find(type == 1); % Index of measurements..
ppi = find(type == 2);
qi = find(type == 3);
pf = find(type == 4);
qf = find(type == 5);
nvi = length(vi); % Number of Voltage measurements..
npi = length(ppi); % Number of Real Power Injection measurements..
nqi = length(qi); % Number of Reactive Power Injection measurements..
npf = length(pf); % Number of Real Power Flow measurements..
nqf = length(qf); % Number of Reactive Power Flow measurements..
% iter = 1;
% tol = 5;
% Jacobian..
% H11 - Derivative of V with respect to angles.. All Zeros
H11 = zeros(nvi,nbus-1);
% H12 - Derivative of V with respect to V..
H12 = zeros(nvi,nbus);
for k = 1:nvi
for n = 1:nbus
if n == k
H12(k,n) = 1;
end
end
end
% H21 - Derivative of Real Power Injections with Angles..
H21 = zeros(npi,nbus-1);
for i = 1:npi
m = fbus(ppi(i));
for k = 1:(nbus-1)
if k+1 == m
for n = 1:nbus
H21(i,k) = H21(i,k) + V(m)* V(n)*(-G(m,n)*sin(del(m)-del(n)) + B(m,n)*cos(del(m)-del(n)));
end
H21(i,k) = H21(i,k) - V(m)^2*B(m,m);
else
H21(i,k) = V(m)* V(k+1)*(G(m,k+1)*sin(del(m)-del(k+1)) - B(m,k+1)*cos(del(m)-del(k+1)));
end
end
end
% H22 - Derivative of Real Power Injections with V..
H22 = zeros(npi,nbus);
for i = 1:npi
m = fbus(ppi(i));
for k = 1:(nbus)
if k == m
for n = 1:nbus
H22(i,k) = H22(i,k) + V(n)*(G(m,n)*cos(del(m)-del(n)) + B(m,n)*sin(del(m)-del(n)));
end
H22(i,k) = H22(i,k) + V(m)*G(m,m);
else
H22(i,k) = V(m)*(G(m,k)*cos(del(m)-del(k)) + B(m,k)*sin(del(m)-del(k)));
end
end
end
% H31 - Derivative of Reactive Power Injections with Angles..
H31 = zeros(nqi,nbus-1);
for i = 1:nqi
m = fbus(qi(i));
for k = 1:(nbus-1)
if k+1 == m
for n = 1:nbus
H31(i,k) = H31(i,k) + V(m)* V(n)*(G(m,n)*cos(del(m)-del(n)) + B(m,n)*sin(del(m)-del(n)));
end
H31(i,k) = H31(i,k) - V(m)^2*G(m,m);
else
H31(i,k) = V(m)* V(k+1)*(-G(m,k+1)*cos(del(m)-del(k+1)) - B(m,k+1)*sin(del(m)-del(k+1)));
end
end
end
% H32 - Derivative of Reactive Power Injections with V..
H32 = zeros(nqi,nbus);
for i = 1:nqi
m = fbus(qi(i));
for k = 1:(nbus)
if k == m
for n = 1:nbus
H32(i,k) = H32(i,k) + V(n)*(G(m,n)*sin(del(m)-del(n)) - B(m,n)*cos(del(m)-del(n)));
end
H32(i,k) = H32(i,k) - V(m)*B(m,m);
else
H32(i,k) = V(m)*(G(m,k)*sin(del(m)-del(k)) - B(m,k)*cos(del(m)-del(k)));
end
end
end
% H41 - Derivative of Real Power Flows with Angles..
H41 = zeros(npf,nbus-1);
for i = 1:npf
m = fbus(pf(i));
n = tbus(pf(i));
for k = 1:(nbus-1)
if k+1 == m
H41(i,k) = V(m)* V(n)*(-G(m,n)*sin(del(m)-del(n)) + B(m,n)*cos(del(m)-del(n)));
else if k+1 == n
H41(i,k) = -V(m)* V(n)*(-G(m,n)*sin(del(m)-del(n)) + B(m,n)*cos(del(m)-del(n)));
else
H41(i,k) = 0;
end
end
end
end
% H42 - Derivative of Real Power Flows with V..
H42 = zeros(npf,nbus);
for i = 1:npf
m = fbus(pf(i));
n = tbus(pf(i));
for k = 1:nbus
if k == m
H42(i,k) = -V(n)*(-G(m,n)*cos(del(m)-del(n)) - B(m,n)*sin(del(m)-del(n))) - 2*G(m,n)*V(m);
else if k == n
H42(i,k) = -V(m)*(-G(m,n)*cos(del(m)-del(n)) - B(m,n)*sin(del(m)-del(n)));
else
H42(i,k) = 0;
end
end
end
end
% H51 - Derivative of Reactive Power Flows with Angles..
H51 = zeros(nqf,nbus-1);
for i = 1:nqf
m = fbus(qf(i));
n = tbus(qf(i));
for k = 1:(nbus-1)
if k+1 == m
H51(i,k) = -V(m)* V(n)*(-G(m,n)*cos(del(m)-del(n)) - B(m,n)*sin(del(m)-del(n)));
else if k+1 == n
H51(i,k) = V(m)* V(n)*(-G(m,n)*cos(del(m)-del(n)) - B(m,n)*sin(del(m)-del(n)));
else
H51(i,k) = 0;
end
end
end
end
% H52 - Derivative of Reactive Power Flows with V..
H52 = zeros(nqf,nbus);
for i = 1:nqf
m = fbus(qf(i));
n = tbus(qf(i));
for k = 1:nbus
if k == m
H52(i,k) = -V(n)*(-G(m,n)*sin(del(m)-del(n)) + B(m,n)*cos(del(m)-del(n))) - 2*V(m)*(-B(m,n)+ bpq(m,n));
else if k == n
H52(i,k) = -V(m)*(-G(m,n)*sin(del(m)-del(n)) + B(m,n)*cos(del(m)-del(n)));
else
H52(i,k) = 0;
end
end
end
end
% Measurement Jacobian, H..
H = [H11 H12; H21 H22; H31 H32; H41 H42; H51 H52];
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。


























 812
812

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










