【SLAM】6非线性优化

补充知识

贝叶斯

怎样用非数学语言讲解贝叶斯定理

• 贝叶斯公式: 先假设一个事件发生的概率, 再用新得到的信息修正它
  • $$P(A|B)=P(A)\frac{P(B|A)}{P(B)}$$
  • 后验概率 = 先验概率 x 调整因子(可能性函数)
• 全概率公式
  • $$P(B)=P(B|A)P(A)+P(B|A^{\prime })P(A^{\prime })$$

似然函数&最大似然估计

详解最大似然估计（MLE）、最大后验概率估计（MAP），以及贝叶斯公式的理解
一文搞懂极大似然估计

• 似然函数:
  • $P(x|\theta )$: $x$:某具体数据, $\theta$:某模型参数
  • $\theta$确定$x$变量: 概率函数, 描述对不同样本点$x$, 其出现概率是多少
  • $x$确定$\theta$变量: 似然函数, 描述对不通模型参数, 出现$x$样本的的概率是多少
• 最大似然估计: 在什么样的状态下, 最可能产生现在观测到的数据
  • 似然: 在现在的位姿下, 可能产生怎样的观测数据
  • 利用已知样本结果信息, 反推最有可能导致这些样本结果出现的模型参数值
  • 条件: 所有采样都是独立同步分布的

齐次矩阵

为什么要引入齐次坐标，齐次坐标的意义（一）

正定矩阵

• 当$X$不是零向量, 有$f=X^{\prime }AX>0$, 这样的二次型称正定的, 对称矩阵$A$称正定矩阵

奇异矩阵

• 矩阵可表示变换, 逆矩阵可表示其逆变换
• 非奇异矩阵: 行列式≠0
• 奇异矩阵: 行列式=0, 没有逆矩阵

6.1.状态估计问题

6.1.1.最大后验估计

• 经典SLAM模型=运动方程+观测方程
  • $\{\begin{array}{l}{\mathbf{x}}_k=f\left({\mathbf{x}}_{k-1},{\mathbf{u}}_k\right)+{\mathbf{w}}_k\\ {\mathbf{z}}_{k,j}=h\left({\mathbf{y}}_j,{\mathbf{x}}_k\right)+{\mathbf{v}}_{k,j}\end{array}$
    • $x_1...x_K$ 各时刻的位置
    • $y_1...y_N$ 路标点
    • $u_k$ 运动传感器的读数/输入
    • $w_k$ 噪声
• 状态估计问题: 假设$x_k$处对路标$y_j$进行了一次观测, 对应到图像上像素位置$z_{k,j}$, 则观测方程
  • $$s{z}_{k,j}=K(R_k{y}_j+t_k)$$
    • $K$: 相机内参
    • $s$: 像素点的距离
    • 假设两个噪声项$w_k,v_{k,j}$满足零均值的高斯分布
  • 通过带噪声的数据$z$和$u$推断位姿$x$和地图$y$ (状态估计问题)
  • 增量方法: 持有一个当前时刻的估计状态, 用新的数据更新它
    • 只关心当前状态, 不考虑
  • 批量方法: 聚集数据, 一起处理
    • SfM, 不实时
  • 滑动窗口估计法: 固定一些历史轨迹, 仅对当前时刻附近一些轨迹进行优化
• 批量方法
  • 概率学角度: 已知输入数据$u$和观测数据$z$条件下, 求状态$x$, $y$的条件概率分布 $P(x,y|z,u)$
  • 问题变为求解最大似然估计
    • $$(\mathbf{x},\mathbf{y}{)}^{\ast }{}_{\mathrm{MLE}}=\arg \max P(\mathbf{z},\mathbf{u}\mid \mathbf{x},\mathbf{y})$$
    • 似然: 在现在的位姿下, 可能产生怎样的观测数据
    • 最大似然估计: 在什么样的状态下, 最可能产生现在观测到的数据

6.1.2.最小二乘

• 最小化负对数求一个高斯分布的最大似然
  • $$\begin{array}{rl}{\left({\mathbf{x}}_k,{\mathbf{y}}_j\right)}^{\ast }& =\arg \max \mathcal{N}\left(h\left({\mathbf{y}}_j,{\mathbf{x}}_k\right),{\mathbf{Q}}_{k,j}\right)\\ & =\arg \min \left({\left({\mathbf{z}}_{k,j}-h\left({\mathbf{x}}_k,{\mathbf{y}}_j\right)\right)}^{\mathrm{T}}{\mathbf{Q}}_{k,j}^{-1}\left({\mathbf{z}}_{k,j}-h\left({\mathbf{x}}_k,{\mathbf{y}}_j\right)\right)\right)\end{array}$$
    • 等价于最小化噪声项的一个二次型: 马哈拉诺比斯距离(马氏距离)
    • 由$Q_{k,j}^{-1}$(信息矩阵)加权后的欧氏距离(高斯分布协方差矩阵的逆)
• 最小二乘问题: 最小化所有时刻估计值与真实读数之间马氏距离<=>求最大似然估计
  • $\min J(\mathbf{x},\mathbf{y})={\sum }_k{\mathbf{e}}_{\mathbf{u},k}^{\mathrm{T}}{\mathbf{R}}_k^{-1}{\mathbf{e}}_{\mathbf{u},k}+{\sum }_k{\sum }_j{\mathbf{e}}_{\mathbf{z},k,j}^{\mathrm{T}}{\mathbf{Q}}_{k,j}^{-1}{\mathbf{e}}_{\mathbf{z},k,j}$
  • 各次输入和观测数据与模型之间的误差$\begin{array}{rl}{e}_{\mathbf{u},k}& ={\mathbf{x}}_k-f\left({\mathbf{x}}_{k-1},{\mathbf{u}}_k\right)\\ e_{\mathbf{z},j,k}& ={\mathbf{z}}_{k,j}-h\left({\mathbf{x}}_k,{\mathbf{y}}_j\right)\end{array}$
  • 由于噪声存在, 估计的轨迹与地图带入SLAM运动, 观测方程时, 不全成立, 需对估计值进行微调使整体误差下降到极小值: 非线性优化

6.1.3.批量状态估计

1. 考虑一个简单离散时间系统
   $$\begin{array}{ll}{\mathbf{x}}_k={\mathbf{x}}_{k-1}+{\mathbf{u}}_k+{\mathbf{w}}_k,& {\mathbf{w}}_k\sim \mathcal{N}\left(0,{\mathbf{Q}}_k\right)\\ {\mathbf{z}}_k={\mathbf{x}}_k+{\mathbf{n}}_k,& {\mathbf{n}}_k\sim \mathcal{N}\left(0,{\mathbf{R}}_k\right)\end{array}$$
   1. 运动方程: $u_k$输入, $w_k$噪声
   2. 观测方程: $z_k$对汽车未知策略, $x_0$已知
2. 最大似然估计
   $$\begin{array}{rl}{\mathbf{x}}_{\text{map }}^{\ast }& =\arg \max P(\mathbf{x}\mid \mathbf{u},\mathbf{z})=\arg \max P(\mathbf{u},\mathbf{z}\mid \mathbf{x})\\ & =\prod _{k=1}^{3}P\left({\mathbf{u}}_k\mid {\mathbf{x}}_{k-1},{\mathbf{x}}_k\right)\prod _{k=1}^{3}P\left({\mathbf{z}}_k\mid {\mathbf{x}}_k\right)\end{array}$$
   1. 令批量状态变量为
      $x=[x_0,x_1,x_2,x_3{]}^T,z=[z_1,z_2,z_3{]}^T,u=[u_1,u_2,u_3{]}^T$
   2. 对于每一项 $$\begin{array}{rl}P(u_k|x_{k-1},x_k)& =\mathcal{N}(x_k-x_{k-1},Q_k)\\ P\left({\mathbf{z}}_k\mid {\mathbf{x}}_k\right)& =\mathcal{N}\left({\mathbf{x}}_k,{\mathbf{R}}_k\right)\end{array}$$
   3. 构建误差变量
      $e_{u,k}=x_k-x_{k-1}-u_k,e_{z,k}=z_k-x_k$
3. 最小二乘目标函数
   $$\min \sum _{k=1}^3{\mathbf{e}}_{\mathbf{u},k}^{\mathrm{T}}{\mathbf{Q}}_k^{-1}{\mathbf{e}}_{\mathbf{u},k}+\sum _{k=1}^3{\mathbf{e}}_{\mathbf{z},k}^{\mathrm{T}}{\mathbf{R}}_k^{-1}{\mathbf{e}}_{\mathbf{z},k}$$
   1. 定义向量 $y=[u,z{]}^T$, 可写出矩阵H使得 $y-Hx=e\sim \mathcal{N}(0,\Sigma )$
   2. 问题变为 $x_{map}^{\ast }=\arg \min e^T{\Sigma }^{-1}e$
   3. 该问题唯一解 $ \boldsymbol{x}_{\text {map }}^{{*}=\left(\boldsymbol{H}}{\mathrm{T}} \boldsymbol{\Sigma}^{-1} \boldsymbol{H}\right)^{-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{\Sigma}^{-1} \boldsymbol{y}$

6.2.非线性最小二乘

• 对最小二乘问题
  $$\underset{\mathbf{x}}{\min }F(\mathbf{x})=\frac{1}{2}||f(\mathbf{x})|{|}_2^2$$
  • 求导函数, 令导数=0, 求解x最优值
  • 对形式复杂的导函数, 迭代法: 求解导函数为零的问题变为不断寻找下降增量$\Delta x_k$的问题
    1. 给定初始值$x_0$
    2. 对第$k$次迭代, 寻找增量$\Delta x_k$使$||f(x_k+\Delta x_k)|{|}_2^2$最小
    3. $\Delta x_k$足够小则停止
    4. 否则令$x_{k+1}=x_k+\Delta x_k$, ->第二步

6.2.1.一阶&二阶梯度法

• 第$k$次迭代, 泰勒展开
  • $$F\left({\mathbf{x}}_k+\Delta {\mathbf{x}}_k\right)\approx F\left({\mathbf{x}}_k\right)+\mathbf{J}{\left({\mathbf{x}}_k\right)}^{\mathrm{T}}\Delta {\mathbf{x}}_k+\frac{1}{2}\Delta {\mathbf{x}}_k^{\mathrm{T}}\mathbf{H}\left({\mathbf{x}}_k\right)\Delta {\mathbf{x}}_k$$
    • $J(x_k)$: $F(x)$关于$x$的一阶导数, 梯度, 雅可比矩阵
    • $H(x_k)$: $F(x)$关于$x$的二阶导数, 海塞矩阵
    • 一阶梯度法
      • 保留一节梯度, 取增量为反向梯度 $\Delta x^{\ast }=-J(x_k)$ , 可保证函数下降
    • 二阶梯度法(牛顿法)
      $\Delta {\mathbf{x}}^{\ast }=\arg \min \left(F(\mathbf{x})+\mathbf{J}(\mathbf{x}{)}^{\mathrm{T}}\Delta \mathbf{x}+\frac{1}{2}\Delta {\mathbf{x}}^{\mathrm{T}}\mathbf{H}\Delta \mathbf{x}\right)$
      • 对右侧求$\Delta x$导得 $\mathbf{J}+\mathbf{H}\Delta \mathbf{x}=0\Rightarrow \mathbf{H}\Delta \mathbf{x}=-\mathbf{J}$

6.2.2.高斯牛顿法

• 高斯牛顿法
  1. 给定初始值$x_0$
  2. 对第$k$次迭代, 求当前雅可比矩阵$J(x_k)$和误差$f(x_k)$
  3. 求解增量方程: $\mathbf{H}\Delta {\mathbf{x}}_k=\mathbf{g}$
  4. 若$\Delta {\mathbf{x}}_k$足够小, 停止; 否则令${\mathbf{x}}_{k+1}={\mathbf{x}}_k+\Delta {\mathbf{x}}_k$
  • 只能在展开点附近有较好的近似效果

6.2.3.列文伯格-马夸尔特方法

• 列文伯格-马夸尔特方法(阻尼牛顿法)
  • 给$\Delta \mathbf{x}$加信赖区域
    • $\rho =\frac{f(\mathbf{x}+\Delta \mathbf{x})-f(\mathbf{x})}{\mathbf{J}(\mathbf{x}{)}^T\Delta \mathbf{x}}$
      • 分子: 实际函数下降值
      • 分母: 近似模型下降值
      • 接近1: 好近似
      • 太小: 实际减小值远小于近似减小值, 近似较差, 缩小范围
      • 太大: 实际下降比预计大, 放大近似范围
  1. 给定初始值${\mathbf{x}}_0$, 初始优化半径$\mu$
  2. 对第$k$次迭代, 在高斯牛顿法基础上加上信赖区域
     $$\underset{\Delta x_k}{\min }\frac{1}{2}||f({\mathbf{x}}_k)+\mathbf{J}({\mathbf{x}}_k^T\Delta {\mathbf{x}}_k|{|}^2,ss.t.||\mathbf{D}\Delta {\mathbf{x}}_k|{|}^2\le \mu$$
     $\mu$:信赖区域半径, $\mathbf{D}$系数矩阵
  3. 计算$\rho$
     $$\rho =\frac{f(\mathbf{x}+\Delta \mathbf{x})-f(\mathbf{x})}{\mathbf{J}(\mathbf{x}{)}^T\Delta \mathbf{x}}$$
  4. 若$\rho >\frac{3}{4}$: 设$\mu =2\mu$ ; 若$\rho <\frac{1}{4}$: 设$\mu =0.5\mu$
  5. 若$\rho$>某与之, 近似可行, 令 ${\mathbf{x}}_{k+1}={\mathbf{x}}_k+\Delta {\mathbf{x}}_k$
  6. 判断算法是否收敛, 收敛结束, 不收敛->2.

通常当问题性质较好时, 用高斯牛顿法; 问题接近病态, 用列-马法

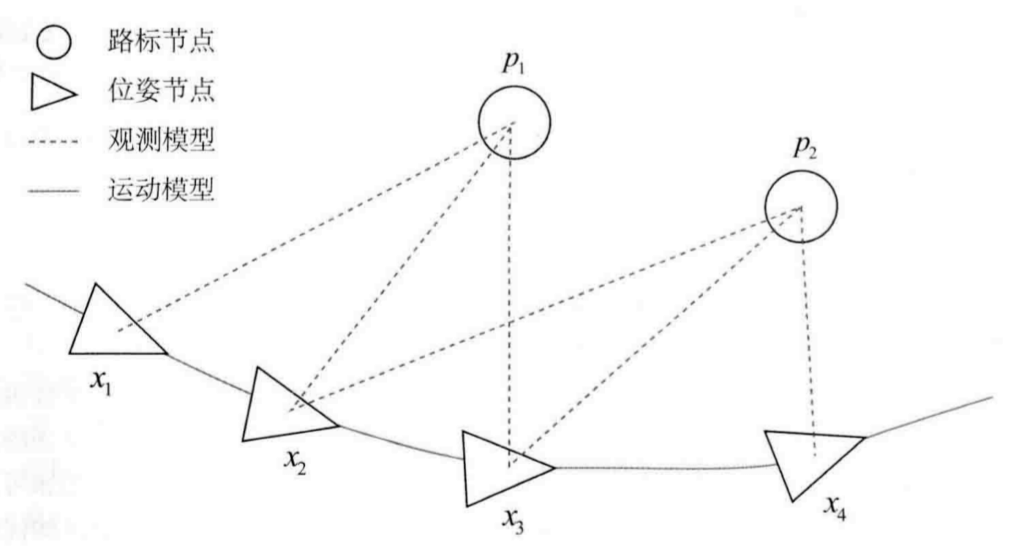
图优化理论

• 图优化: 把优化问题表现成图的一种方式
• 图: 图论的图
  • 顶点: 优化变量
  • 边: 误差项
  • 
• 曲线拟合
  • 只有一个顶点
  • 边都是一元边: 只连接一个顶点
  • 优化步骤
    1. 定义顶点与边的类型
    2. 构建图
    3. 选择优化算法
    4. 调用g2o优化, 返回结果
• C++类继承
• 虚函数

实现

ref

• Ceres库安装踩坑（SLAM十四讲）
• undefined reference to `ceres::Problem::Problem()
  • CMakeLists.txt添加
    main.cpp

#include <iostream>
#include <opencv2/opencv.hpp>
#include <opencv2/core/core.hpp>
#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Dense>

#include <ceres/ceres.h>

#include <g2o/core/g2o_core_api.h>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/core/optimization_algorithm_dogleg.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <cmath>

// #include <chrono>
using namespace std;
using namespace Eigen;
int GaussNewton();
int CeresCurveFit();

int main(int argc, char **argv) {
    // GaussNewton();
    CeresCurveFit();
    return 0;
}

int GaussNewton()
{
    double ar = 1.0, br = 2.0, cr = 1.0;    // 真实参数值
    double ae = 2.0, be = -1.0, ce = 5.0;   // 估计参数值
    int N = 100;                            // 数据点
    double w_sigma = 1.0;                   // 噪声Sigma值
    double inv_sigma = 1.0 / w_sigma;
    cv::RNG rng;                            // OpenCV随机数生成器

    vector<double> x_data, y_data;
    for(int i=0; i<N; i++)
    {
        double x = i/100.0;
        x_data.push_back(x);
        y_data.push_back(exp(ar*x*x + br*x + cr) + rng.gaussian(w_sigma*w_sigma));
    }

    // Gauss-Newton Iteration
    int iterations = 100;
    double Cost = 0, LastCost = 0;
    for(int iter = 0; iter<iterations; iter++)
    {
        Matrix3d H = Matrix3d::Zero();
        Vector3d b = Vector3d::Zero();
        Cost = 0;
        for(int i=0; i<N; i++)
        {
            double xi = x_data[i], yi = y_data[i];  //  数据点1
            double error = yi - exp(ae*xi*xi + be*xi + ce);
            Vector3d J;     //  雅可比矩阵
            J[0] = -xi*xi * exp(ae*xi*xi + be*xi + ce);
            J[1] = -xi * exp(ae*xi*xi + be*xi + ce);
            J[2] = -exp(ae*xi*xi + be*xi + ce);

            H += inv_sigma*inv_sigma*J*J.transpose();
            b += -inv_sigma*inv_sigma*error*J;
            Cost += error*error;
        }

        Vector3d dx = H.ldlt().solve(b);
        
        if(iter > 0 && Cost >= LastCost)
        {
            cout << "Cost:" << Cost << " >= LastCost " << LastCost << endl;
            break;
        }

        ae += dx[0];
        be += dx[1];
        ce += dx[2];

        LastCost = Cost;
        cout << "iteration" << iter << "times" << endl;
    }
    cout << "estimate abc = " << ae << ", " << be << ", " << ce << ", " << endl;
}

struct CURVE_FITTING_COST
{
    CURVE_FITTING_COST(double x, double y) : _x(x), _y(y) {}
    template<typename T>
    bool operator()(const T *const abc, T *residual) const {
        residual[0] = T(_y) - ceres::exp(abc[0]*T(_x)*T(_x) + abc[1]*T(_x) + abc[2]);
        return true;
    }
    const double _x, _y;
};
int CeresCurveFit()
{
    double ar = 1.0, br = 2.0, cr = 1.0;    // 真实参数值
    double ae = 2.0, be = -1.0, ce = 5.0;   // 估计参数值
    int N = 100;                            // 数据点
    double w_sigma = 1.0;                   // 噪声Sigma值
    double inv_sigma = 1.0 / w_sigma;
    cv::RNG rng;                            // OpenCV随机数生成器

    vector<double> x_data, y_data;
    for(int i=0; i<N; i++)
    {
        double x = i/100.0;
        x_data.push_back(x);
        y_data.push_back(exp(ar*x*x + br*x + cr) + rng.gaussian(w_sigma*w_sigma));
    }

    double abc[3] = {ae, be, ce};
    ceres::Problem problem;
    for(int i=0; i<N; i++)
    {
        problem.AddResidualBlock(
            new ceres::AutoDiffCostFunction<CURVE_FITTING_COST, 1, 3>(
                new CURVE_FITTING_COST(x_data[i], y_data[i])
            ),
            nullptr,
            abc
        );
    }
    ceres::Solver::Options options;
    options.linear_solver_type = ceres::DENSE_NORMAL_CHOLESKY;
    options.minimizer_progress_to_stdout = true;
    ceres::Solver::Summary summary;
    ceres::Solve(options, &problem, &summary);
    cout << summary.BriefReport() << endl;
    for(auto a:abc)cout << a << " ";
}

class CurveFittingVertex : public g2o::BaseVertex<3, Eigen::Vector3d>{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    virtual void setToOriginImpl()override{
        _estimate << 0,0,0;
    }
    virtual void oplusImpl(const double *update)override{
        _estimate += Eigen::Vector3d(update);
    }
    virtual bool read(istream &in){}
    virtual bool write(ostream &out)const{}
};

class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}
    virtual void computeError() override{
        const CurveFittingVertex *v = static_cast<const CurveFittingVertex *>(_vertices[0]);
        const Eigen::Vector3d abc = v->estimate();
        _error(0,0) = _measurement - std::exp(abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0));
    }
    virtual void linearizeOplus() override{
        const CurveFittingVertex *v = static_cast<const CurveFittingVertex *>(_vertices[0]);
        const Eigen::Vector3d abc = v->estimate();
        double y = exp(abc[0]*_x*_x + abc[1]*_x + abc[2]);
        _jacobianOplusXi[0] = -_x*_x*y;
        _jacobianOplusXi[1] = -_x*y;
        _jacobianOplusXi[2] = -y;
    }
    virtual bool read(istream &in){}
    virtual bool write(ostream &out)const{}
public:
    double _x;
};

int g20CurveFitting()
{
    double ar = 1.0, br = 2.0, cr = 1.0;    // 真实参数值
    double ae = 2.0, be = -1.0, ce = 5.0;   // 估计参数值
    int N = 100;                            // 数据点
    double w_sigma = 1.0;                   // 噪声Sigma值
    double inv_sigma = 1.0 / w_sigma;
    cv::RNG rng;                            // OpenCV随机数生成器

    vector<double> x_data, y_data;
    for(int i=0; i<N; i++)
    {
        double x = i/100.0;
        x_data.push_back(x);
        y_data.push_back(exp(ar*x*x + br*x + cr) + rng.gaussian(w_sigma*w_sigma));
    }

    typedef g2o::BlockSolver<g2o::BlockSolverTraits<3,1>> BlockSolverType;
    typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;
    auto solver = new g2o::OptimizationAlgorithmGaussNewton(
        g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
    g2o::SparseOptimizer optimizer;
    optimizer.setAlgorithm(solver);
    optimizer.setVerbose(true);

    CurveFittingVertex *v = new CurveFittingVertex();
    v->setEstimate(Eigen::Vector3d(ae,be,ce));
    v->setId(0);
    optimizer.addVertex(v);
    for(int i=0; i<N; i++)
    {
        CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
        edge->setId(i);
        edge->setVertex(0,v);
        edge->setMeasurement(y_data[i]);
        edge->setInformation(Eigen::Matrix<double,1,1>::Identity() * 1 / (w_sigma*w_sigma));
        optimizer.addEdge(edge);
    }
    
    optimizer.initializeOptimization();
    optimizer.optimize(10);
    Eigen::Vector3d abc_estimate = v->estimate();
    cout << "estimated model: " << abc_estimate.transpose();

}

CMakeLists.txt

cmake_minimum_required(VERSION 2.6)
project(test_optimize)

add_executable(test_optimize main.cpp)
find_package(OpenCV REQUIRED)
find_package(Ceres REQUIRED)
install(TARGETS test_optimize RUNTIME DESTINATION bin)
target_link_libraries(test_optimize ${OpenCV_LIBS})
target_link_libraries(test_optimize ${CERES_LIBRARIES})
target_link_libraries(test_optimize ${G2O_LIBS})